Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Обучение многообразию на рукописных цифрах: Locally Linear Embedding, Isomap…#
Мы демонстрируем различные техники вложения на наборе данных digits.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Загрузить набор данных цифр#
Мы загрузим набор данных digits и будем использовать только шесть первых из десяти доступных классов.
from sklearn.datasets import load_digits
digits = load_digits(n_class=6)
X, y = digits.data, digits.target
n_samples, n_features = X.shape
n_neighbors = 30
Мы можем построить первые сто цифр из этого набора данных.
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(6, 6))
for idx, ax in enumerate(axs.ravel()):
ax.imshow(X[idx].reshape((8, 8)), cmap=plt.cm.binary)
ax.axis("off")
_ = fig.suptitle("A selection from the 64-dimensional digits dataset", fontsize=16)

Вспомогательная функция для построения вложения#
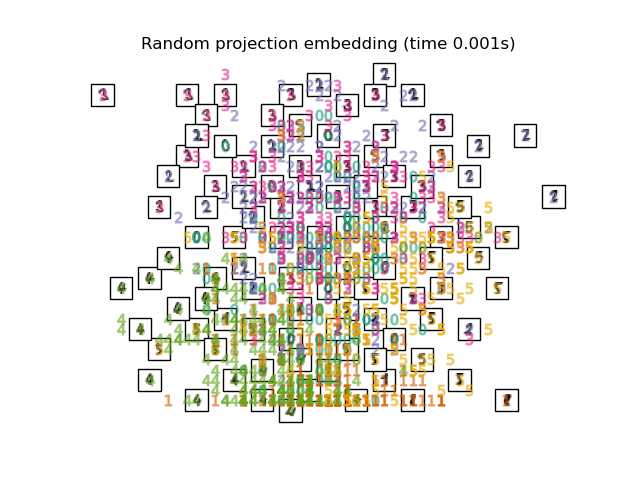
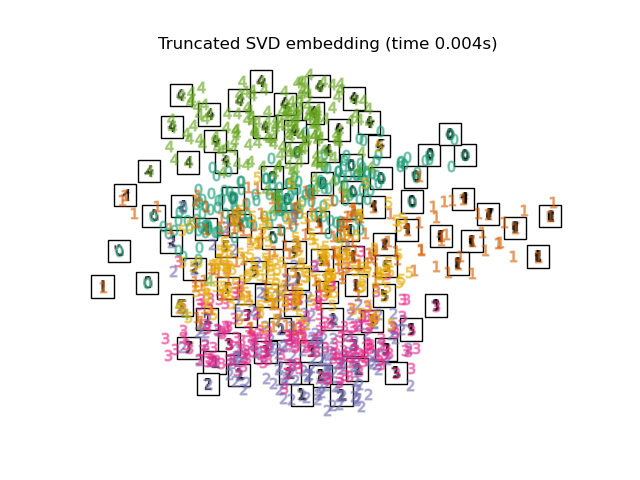
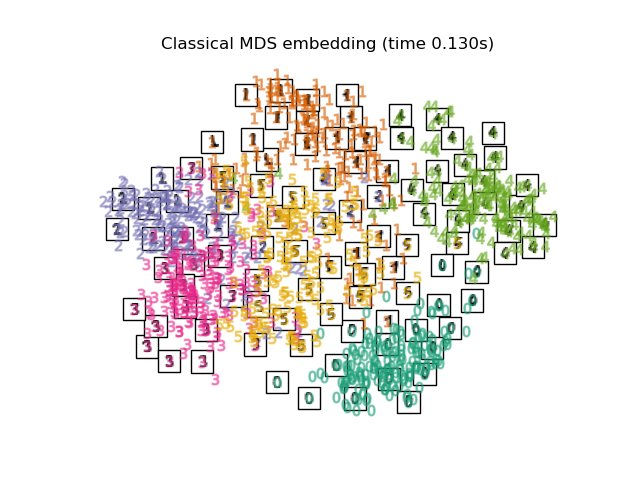
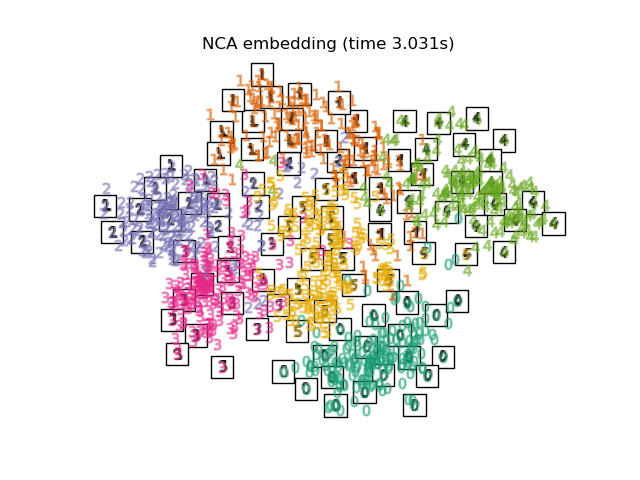
Ниже мы будем использовать различные техники для вложения набора данных цифр. Мы построим проекцию исходных данных на каждое вложение. Это позволит нам проверить, группируются ли цифры вместе во вложенном пространстве или разбросаны по нему.
import numpy as np
from matplotlib import offsetbox
from sklearn.preprocessing import MinMaxScaler
def plot_embedding(X, title):
_, ax = plt.subplots()
X = MinMaxScaler().fit_transform(X)
for digit in digits.target_names:
ax.scatter(
*X[y == digit].T,
marker=f"${digit}$",
s=60,
color=plt.cm.Dark2(digit),
alpha=0.425,
zorder=2,
)
shown_images = np.array([[1.0, 1.0]]) # just something big
for i in range(X.shape[0]):
# plot every digit on the embedding
# show an annotation box for a group of digits
dist = np.sum((X[i] - shown_images) ** 2, 1)
if np.min(dist) < 4e-3:
# don't show points that are too close
continue
shown_images = np.concatenate([shown_images, [X[i]]], axis=0)
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r), X[i]
)
imagebox.set(zorder=1)
ax.add_artist(imagebox)
ax.set_title(title)
ax.axis("off")
Сравнение методов встраивания#
Ниже мы сравниваем различные техники. Однако есть несколько моментов, которые следует отметить:
the
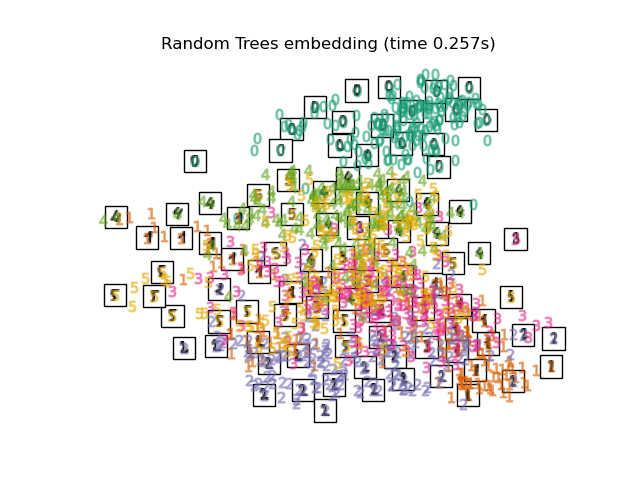
RandomTreesEmbeddingне является технически методом вложения многообразий, так как он изучает высокоразмерное представление, к которому применяется метод снижения размерности. Однако часто полезно преобразовать набор данных в представление, в котором классы линейно разделимы.the
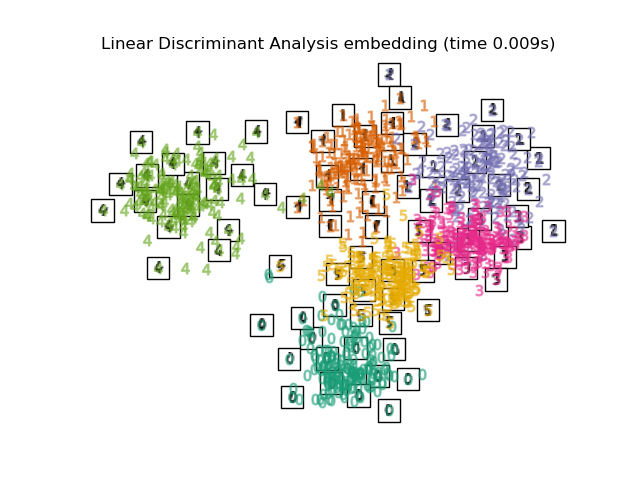
LinearDiscriminantAnalysisиNeighborhoodComponentsAnalysisявляются методами контролируемого понижения размерности, т.е. они используют предоставленные метки, в отличие от других методов.the
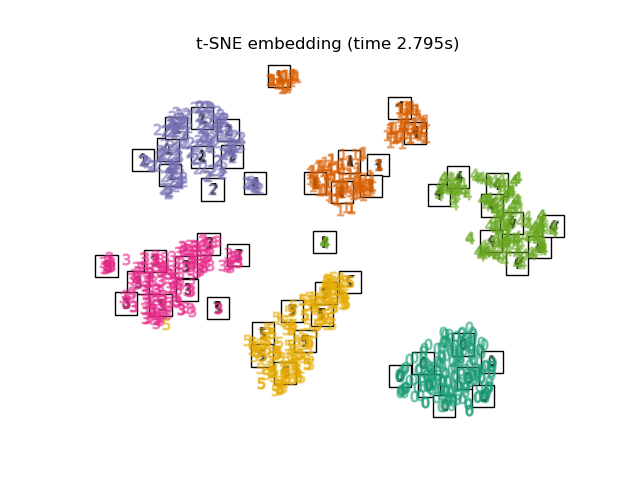
TSNEинициализируется встраиванием, сгенерированным PCA в этом примере. Это обеспечивает глобальную стабильность встраивания, т.е., встраивание не зависит от случайной инициализации.
from sklearn.decomposition import TruncatedSVD
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.ensemble import RandomTreesEmbedding
from sklearn.manifold import (
MDS,
TSNE,
ClassicalMDS,
Isomap,
LocallyLinearEmbedding,
SpectralEmbedding,
)
from sklearn.neighbors import NeighborhoodComponentsAnalysis
from sklearn.pipeline import make_pipeline
from sklearn.random_projection import SparseRandomProjection
embeddings = {
"Random projection embedding": SparseRandomProjection(
n_components=2, random_state=42
),
"Truncated SVD embedding": TruncatedSVD(n_components=2),
"Linear Discriminant Analysis embedding": LinearDiscriminantAnalysis(
n_components=2
),
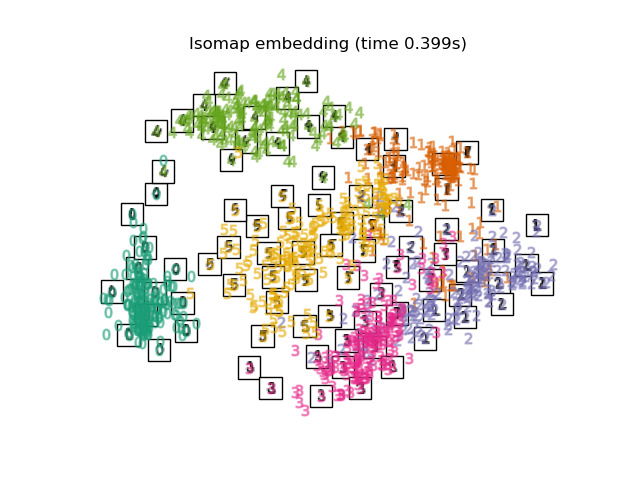
"Isomap embedding": Isomap(n_neighbors=n_neighbors, n_components=2),
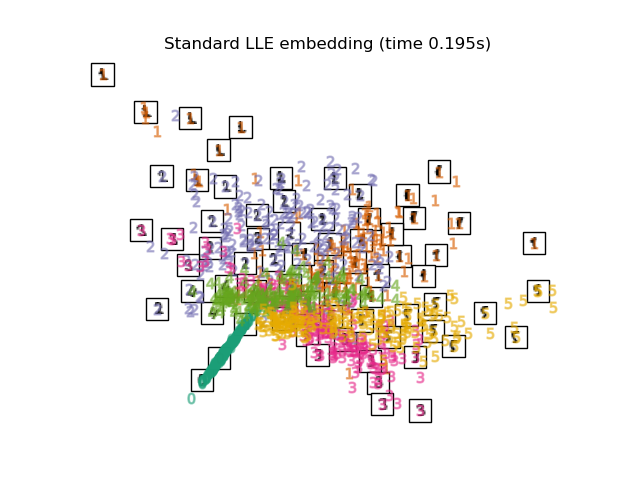
"Standard LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="standard"
),
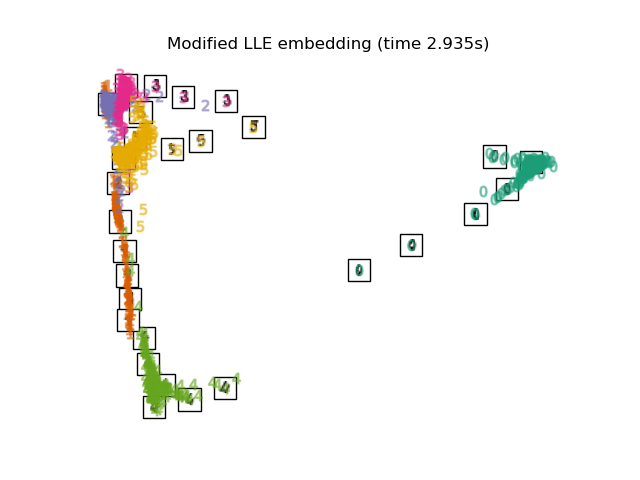
"Modified LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="modified"
),
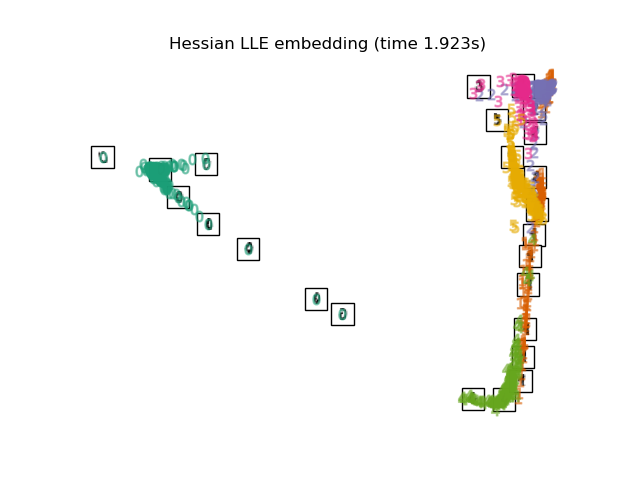
"Hessian LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="hessian"
),
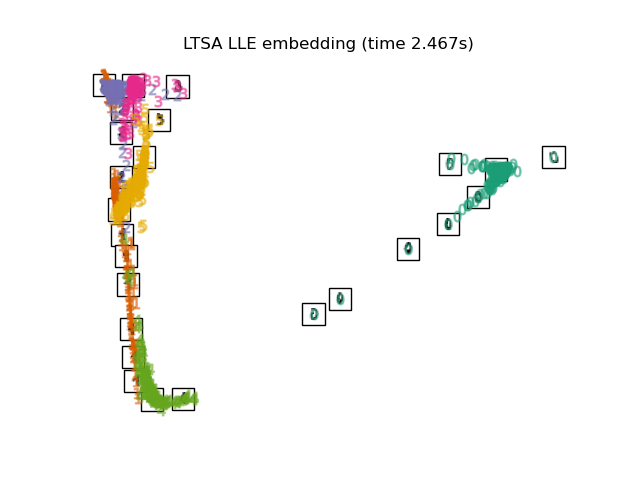
"LTSA LLE embedding": LocallyLinearEmbedding(
n_neighbors=n_neighbors, n_components=2, method="ltsa"
),
"Metric MDS embedding": MDS(n_components=2, n_init=1, init="classical_mds"),
"Non-metric MDS embedding": MDS(
n_components=2, n_init=1, init="classical_mds", metric_mds=False
),
"Classical MDS embedding": ClassicalMDS(n_components=2),
"Random Trees embedding": make_pipeline(
RandomTreesEmbedding(n_estimators=200, max_depth=5, random_state=0),
TruncatedSVD(n_components=2),
),
"Spectral embedding": SpectralEmbedding(
n_components=2, random_state=0, eigen_solver="arpack"
),
"t-SNE embedding": TSNE(
n_components=2,
max_iter=500,
n_iter_without_progress=150,
n_jobs=2,
random_state=0,
),
"NCA embedding": NeighborhoodComponentsAnalysis(
n_components=2, init="pca", random_state=0
),
}
После объявления всех интересующих методов мы можем запустить и выполнить проекцию исходных данных. Мы сохраним спроецированные данные, а также вычислительное время, необходимое для выполнения каждой проекции.
from time import time
projections, timing = {}, {}
for name, transformer in embeddings.items():
if name.startswith("Linear Discriminant Analysis"):
data = X.copy()
data.flat[:: X.shape[1] + 1] += 0.01 # Make X invertible
else:
data = X
print(f"Computing {name}...")
start_time = time()
projections[name] = transformer.fit_transform(data, y)
timing[name] = time() - start_time
Computing Random projection embedding...
Computing Truncated SVD embedding...
Computing Linear Discriminant Analysis embedding...
Computing Isomap embedding...
Computing Standard LLE embedding...
Computing Modified LLE embedding...
Computing Hessian LLE embedding...
Computing LTSA LLE embedding...
Computing Metric MDS embedding...
Computing Non-metric MDS embedding...
Computing Classical MDS embedding...
Computing Random Trees embedding...
Computing Spectral embedding...
Computing t-SNE embedding...
Computing NCA embedding...
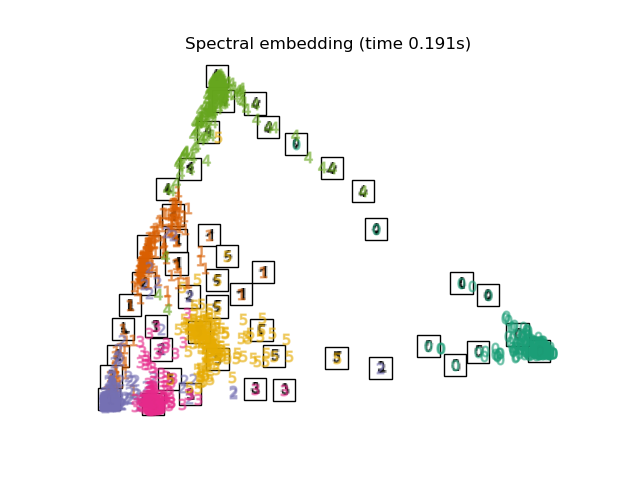
Наконец, мы можем построить результирующую проекцию, полученную каждым методом.
for name in timing:
title = f"{name} (time {timing[name]:.3f}s)"
plot_embedding(projections[name], title)
plt.show()
Общее время выполнения скрипта: (0 минут 42.997 секунд)
Связанные примеры
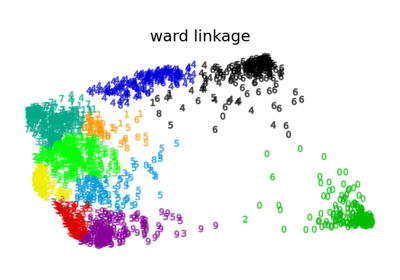
Различные агломеративные кластеризации на 2D-вложении цифр