Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Сравнение ядерной гребневой регрессии и регрессии по методу Гауссовских процессов#

Этот пример иллюстрирует различия между ядерной регрессией Риджа и регрессией Гауссовского процесса.

Как ядерная гребневая регрессия, так и гауссовская процессная регрессия используют так называемый «ядерный трюк», чтобы сделать свои модели достаточно выразительными для подгонки под обучающие данные. Однако задачи машинного обучения, решаемые этими двумя методами, кардинально различаются.

Регрессия ядерного гребня найдёт целевую функцию, которая минимизирует функцию потерь (среднеквадратичную ошибку).

Вместо поиска единой целевой функции, гауссовский процесс регрессии использует вероятностный подход: гауссовское апостериорное распределение над целевыми функциями определяется на основе теоремы Байеса. Таким образом, априорные вероятности целевых функций комбинируются с функцией правдоподобия, определенной наблюдаемыми обучающими данными, для получения оценок апостериорных распределений.

Мы проиллюстрируем эти различия на примере и также сосредоточимся на настройке гиперпараметров ядра.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Генерация набора данных#

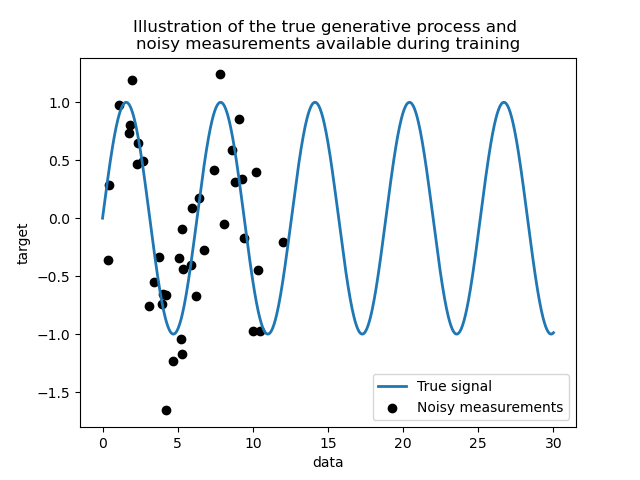
Мы создаем синтетический набор данных. Истинный процесс генерации возьмет 1-D вектор и вычислит его синус. Обратите внимание, что период этого синуса, таким образом, \(2 \pi\). Мы будем повторно использовать эту информацию позже в этом примере.

import numpy as np

rng = np.random.RandomState(0)
data = np.linspace(0, 30, num=1_000).reshape(-1, 1)
target = np.sin(data).ravel()

Теперь мы можем представить сценарий, где мы получаем наблюдения из этого истинного процесса. Однако мы добавим некоторые сложности:

измерения будут зашумленными;
только выборки из начала сигнала будут доступны.

training_sample_indices = rng.choice(np.arange(0, 400), size=40, replace=False)
training_data = data[training_sample_indices]
training_noisy_target = target[training_sample_indices] + 0.5 * rng.randn(
    len(training_sample_indices)
)

Построим истинный сигнал и зашумленные измерения, доступные для обучения.

import matplotlib.pyplot as plt

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Illustration of the true generative process and \n"
    "noisy measurements available during training"
)

Illustration of the true generative process and noisy measurements available during training

Ограничения простой линейной модели#

Сначала мы хотели бы выделить ограничения линейной модели, учитывая наш набор данных. Мы обучаем Ridge и проверить предсказания этой модели на нашем наборе данных.

from sklearn.linear_model import Ridge

ridge = Ridge().fit(training_data, training_noisy_target)

plt.plot(data, target, label="True signal", linewidth=2)
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(data, ridge.predict(data), label="Ridge regression")
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Limitation of a linear model such as ridge")

Limitation of a linear model such as ridge

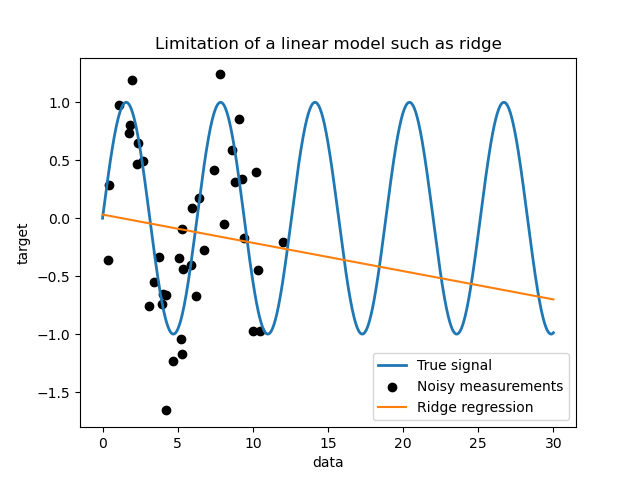
Такой гребневый регрессор недообучает данные, поскольку недостаточно выразителен.

Методы ядра: гребневая регрессия с ядром и гауссовский процесс#

Ядерный гребень#

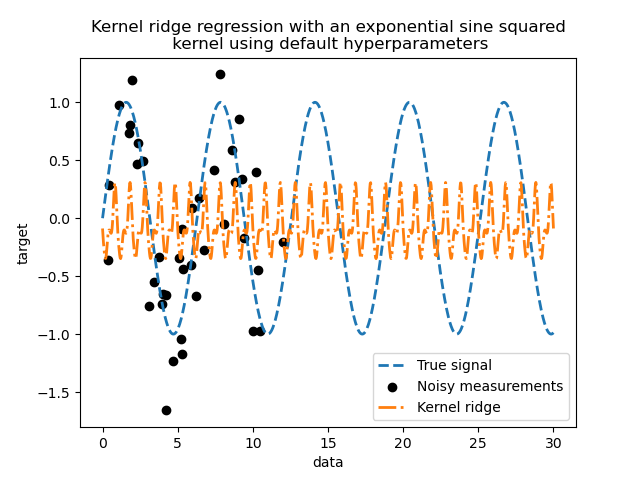
Мы можем сделать предыдущую линейную модель более выразительной, используя так называемое ядро. Ядро — это вложение из исходного пространства признаков в другое. Проще говоря, оно используется для отображения исходных данных в новое и более сложное пространство признаков. Это новое пространство явно определяется выбором ядра.

В нашем случае мы знаем, что истинный процесс генерации является периодической функцией. Мы можем использовать ExpSineSquared ядро которое позволяет восстановить периодичность. Класс KernelRidge будет принимать такое ядро.

Использование этой модели вместе с ядром эквивалентно встраиванию данных с помощью функции отображения ядра и последующему применению гребневой регрессии. На практике данные не отображаются явно; вместо этого скалярное произведение между образцами в пространстве признаков более высокой размерности вычисляется с помощью «ядерного трюка».

Таким образом, давайте используем такой KernelRidge.

import time

from sklearn.gaussian_process.kernels import ExpSineSquared
from sklearn.kernel_ridge import KernelRidge

kernel_ridge = KernelRidge(kernel=ExpSineSquared())

start_time = time.time()
kernel_ridge.fit(training_data, training_noisy_target)
print(
    f"Fitting KernelRidge with default kernel: {time.time() - start_time:.3f} seconds"
)

Fitting KernelRidge with default kernel: 0.001 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    kernel_ridge.predict(data),
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Kernel ridge regression with an exponential sine squared\n "
    "kernel using default hyperparameters"
)

Kernel ridge regression with an exponential sine squared kernel using default hyperparameters

#23548

kernel_ridge.kernel

ExpSineSquared(length_scale=1, periodicity=1)

Наше ядро имеет два параметра: масштаб длины и периодичность. Для нашего набора данных мы используем sin как порождающий процесс, подразумевая \(2 \pi\)-периодичность для сигнала. Значение параметра по умолчанию \(1\), это объясняет высокую частоту, наблюдаемую в прогнозах нашей модели. Аналогичные выводы можно сделать с параметром длины масштаба. Таким образом, это говорит нам, что параметры ядра необходимо настроить. Мы будем использовать рандомизированный поиск для настройки различных параметров модели ядерного гребня: alpha параметр и параметры ядра.

from scipy.stats import loguniform

from sklearn.model_selection import RandomizedSearchCV

param_distributions = {
    "alpha": loguniform(1e0, 1e3),
    "kernel__length_scale": loguniform(1e-2, 1e2),
    "kernel__periodicity": loguniform(1e0, 1e1),
}
kernel_ridge_tuned = RandomizedSearchCV(
    kernel_ridge,
    param_distributions=param_distributions,
    n_iter=500,
    random_state=0,
)
start_time = time.time()
kernel_ridge_tuned.fit(training_data, training_noisy_target)
print(f"Time for KernelRidge fitting: {time.time() - start_time:.3f} seconds")

Time for KernelRidge fitting: 4.354 seconds

Обучение модели теперь более вычислительно затратно, поскольку мы должны попробовать несколько комбинаций гиперпараметров. Мы можем взглянуть на найденные гиперпараметры, чтобы получить некоторое представление.

kernel_ridge_tuned.best_params_

{'alpha': np.float64(1.991584977345022), 'kernel__length_scale': np.float64(0.7986499491396734), 'kernel__periodicity': np.float64(6.6072758064261095)}

Глядя на лучшие параметры, мы видим, что они отличаются от значений по умолчанию. Мы также видим, что периодичность ближе к ожидаемому значению: \(2 \pi\). Теперь мы можем проверить предсказания нашего настроенного ядерного гребня.

start_time = time.time()
predictions_kr = kernel_ridge_tuned.predict(data)
print(f"Time for KernelRidge predict: {time.time() - start_time:.3f} seconds")

Time for KernelRidge predict: 0.002 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title(
    "Kernel ridge regression with an exponential sine squared\n "
    "kernel using tuned hyperparameters"
)

Kernel ridge regression with an exponential sine squared kernel using tuned hyperparameters

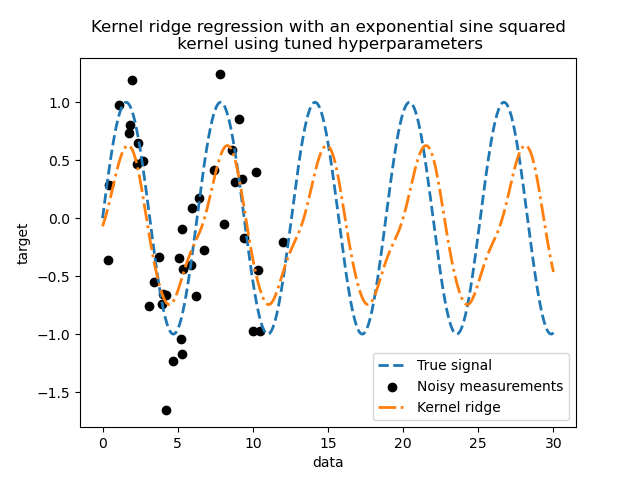
Мы получаем гораздо более точную модель. Мы всё ещё наблюдаем некоторые ошибки, в основном из-за шума, добавленного в набор данных.

Гауссовский процесс регрессии#

Теперь мы будем использовать GaussianProcessRegressor для обучения на одном наборе данных. При обучении гауссовского процесса гиперпараметры ядра оптимизируются в процессе подгонки. Нет необходимости во внешнем поиске гиперпараметров. Здесь мы создаем немного более сложное ядро, чем для регрессора с ядром: добавляем WhiteKernel который используется для оценки шума в наборе данных.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import WhiteKernel

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) + WhiteKernel(
    1e-1
)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
start_time = time.time()
gaussian_process.fit(training_data, training_noisy_target)
print(
    f"Time for GaussianProcessRegressor fitting: {time.time() - start_time:.3f} seconds"
)

Time for GaussianProcessRegressor fitting: 0.044 seconds

Вычислительная стоимость обучения гауссовского процесса намного меньше, чем ядерного гребня, использующего рандомизированный поиск. Мы можем проверить параметры ядер, которые мы вычислили.

gaussian_process.kernel_

0.675**2 * ExpSineSquared(length_scale=1.34, periodicity=6.57) + WhiteKernel(noise_level=0.182)

Действительно, мы видим, что параметры были оптимизированы. Глядя на periodicity параметра, мы видим, что нашли период, близкий к теоретическому значению \(2 \pi\). Теперь мы можем взглянуть на предсказания нашей модели.

start_time = time.time()
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)
print(
    f"Time for GaussianProcessRegressor predict: {time.time() - start_time:.3f} seconds"
)

Time for GaussianProcessRegressor predict: 0.003 seconds

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# Plot the predictions of the kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# Plot the predictions of the gaussian process regressor
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Comparison between kernel ridge and gaussian process regressor")

Comparison between kernel ridge and gaussian process regressor

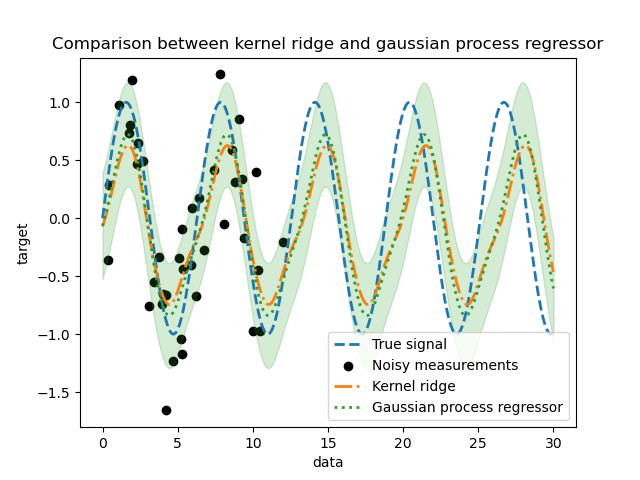
Мы наблюдаем, что результаты ядерного гребня и гауссовского процесса регрессии близки. Однако гауссовский процесс регрессии также предоставляет информацию о неопределённости, которая недоступна при ядерном гребне. Из-за вероятностной формулировки целевых функций, гауссовский процесс может выводить стандартное отклонение (или ковариацию) вместе со средними предсказаниями целевых функций.

Однако это имеет свою цену: время вычисления предсказаний больше с гауссовским процессом.

Итоговый вывод#

Мы можем сделать окончательный вывод относительно возможности двух моделей экстраполировать. Действительно, мы предоставили только начало сигнала в качестве обучающего набора. Использование периодического ядра заставляет нашу модель повторять паттерн, найденный в обучающем наборе. Используя эту информацию о ядре вместе со способностью обеих моделей к экстраполяции, мы наблюдаем, что модели будут продолжать предсказывать синусоидальный паттерн.

Гауссовский процесс позволяет комбинировать ядра вместе. Таким образом, мы могли бы связать ядро экспоненциального синуса в квадрате вместе с ядром радиальной базисной функции.

from sklearn.gaussian_process.kernels import RBF

kernel = 1.0 * ExpSineSquared(1.0, 5.0, periodicity_bounds=(1e-2, 1e1)) * RBF(
    length_scale=15, length_scale_bounds="fixed"
) + WhiteKernel(1e-1)
gaussian_process = GaussianProcessRegressor(kernel=kernel)
gaussian_process.fit(training_data, training_noisy_target)
mean_predictions_gpr, std_predictions_gpr = gaussian_process.predict(
    data,
    return_std=True,
)

plt.plot(data, target, label="True signal", linewidth=2, linestyle="dashed")
plt.scatter(
    training_data,
    training_noisy_target,
    color="black",
    label="Noisy measurements",
)
# Plot the predictions of the kernel ridge
plt.plot(
    data,
    predictions_kr,
    label="Kernel ridge",
    linewidth=2,
    linestyle="dashdot",
)
# Plot the predictions of the gaussian process regressor
plt.plot(
    data,
    mean_predictions_gpr,
    label="Gaussian process regressor",
    linewidth=2,
    linestyle="dotted",
)
plt.fill_between(
    data.ravel(),
    mean_predictions_gpr - std_predictions_gpr,
    mean_predictions_gpr + std_predictions_gpr,
    color="tab:green",
    alpha=0.2,
)
plt.legend(loc="lower right")
plt.xlabel("data")
plt.ylabel("target")
_ = plt.title("Effect of using a radial basis function kernel")

Effect of using a radial basis function kernel

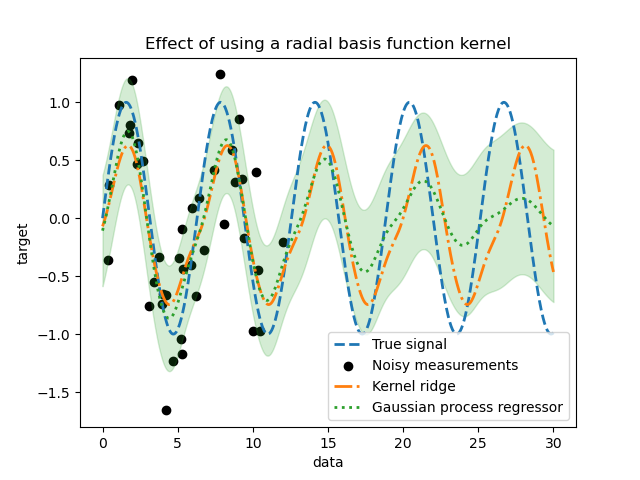
Эффект использования ядра радиальной базисной функции будет ослаблять периодичность, когда в обучающей выборке нет доступных образцов. По мере удаления тестовых образцов от обучающих, предсказания сходятся к их среднему значению, а их стандартное отклонение также увеличивается.

Общее время выполнения скрипта: (0 минут 5.003 секунд)