RBF#
- класс sklearn.gaussian_process.kernels.RBF(length_scale=1.0, ARD также известен в литературе как=(1e-05, 100000.0))[источник]#
Радиально-базисная функция ядра (также известная как квадратно-экспоненциальное ядро).
Ядро RBF является стационарным ядром. Также известно как ядро «квадратичной экспоненты». Параметризуется параметром масштаба длины \(l>0\), который может быть либо скаляром (изотропный вариант ядра), либо вектором с тем же количеством измерений, что и входные данные X (анизотропный вариант ядра). Ядро задаётся формулой:
\[k(x_i, x_j) = \exp\left(- \frac{d(x_i, x_j)^2}{2l^2} \right)\]где \(l\) это масштаб длины ядра и \(d(\cdot,\cdot)\) является евклидовым расстоянием. Для советов по установке параметра масштаба длины см., например, [1].
Это ядро бесконечно дифференцируемо, что подразумевает, что гауссовские процессы с этим ядром в качестве ковариационной функции имеют среднеквадратичные производные всех порядков и, следовательно, очень гладкие. См. [2], Глава 4, Раздел 4.2, для дополнительных деталей о ядре RBF.
Подробнее в Руководство пользователя.
Добавлено в версии 0.18.
- Параметры:
- length_scalefloat или ndarray формы (n_features,), по умолчанию=1.0
Масштаб длины ядра. Если float, используется изотропное ядро. Если массив, используется анизотропное ядро, где каждое измерение l определяет масштаб длины соответствующего измерения признака.
- ARD также известен в литературе какпара чисел с плавающей запятой >= 0 или "fixed", по умолчанию=(1e-5, 1e5)
Нижняя и верхняя граница для 'length_scale'. Если установлено "fixed", 'length_scale' не может быть изменен во время настройки гиперпараметров.
Ссылки
Примеры
>>> from sklearn.datasets import load_iris >>> from sklearn.gaussian_process import GaussianProcessClassifier >>> from sklearn.gaussian_process.kernels import RBF >>> X, y = load_iris(return_X_y=True) >>> kernel = 1.0 * RBF(1.0) >>> gpc = GaussianProcessClassifier(kernel=kernel, ... random_state=0).fit(X, y) >>> gpc.score(X, y) 0.9866 >>> gpc.predict_proba(X[:2,:]) array([[0.8354, 0.03228, 0.1322], [0.7906, 0.0652, 0.1441]])
- __call__(X, Y=None, eval_gradient=False)[источник]#
Возвращает ядро k(X, Y) и, опционально, его градиент.
- Параметры:
- Xndarray формы (n_samples_X, n_features)
Левый аргумент возвращаемого ядра k(X, Y)
- Yndarray формы (n_samples_Y, n_features), по умолчанию=None
Правый аргумент возвращаемого ядра k(X, Y). Если None, вместо этого вычисляется k(X, X).
- eval_gradientbool, по умолчанию=False
Определяет, вычисляется ли градиент относительно логарифма гиперпараметра ядра. Поддерживается только когда Y равен None.
- Возвращает:
- Kndarray формы (n_samples_X, n_samples_Y)
Страница бенчмарков
- K_gradientndarray формы (n_samples_X, n_samples_X, n_dims), необязательный
Градиент ядра k(X, X) по логарифму гиперпараметра ядра. Возвращается только когда
eval_gradientравно True.
- свойство границы#
Возвращает логарифмически преобразованные границы для theta.
- Возвращает:
- границыndarray формы (n_dims, 2)
Логарифмически преобразованные границы гиперпараметров theta ядра
- clone_with_theta(theta)[источник]#
Возвращает клон self с заданными гиперпараметрами theta.
- Параметры:
- thetandarray формы (n_dims,)
Гиперпараметры
- диаг(X)[источник]#
Возвращает диагональ ядра k(X, X).
Результат этого метода идентичен np.diag(self(X)); однако он может быть вычислен более эффективно, так как вычисляется только диагональ.
- Параметры:
- Xndarray формы (n_samples_X, n_features)
Левый аргумент возвращаемого ядра k(X, Y)
- Возвращает:
- K_diagndarray формы (n_samples_X,)
Диагональ ядра k(X, X)
- get_params(глубокий=True)[источник]#
Получить параметры этого ядра.
- Параметры:
- глубокийbool, по умолчанию=True
Если True, вернет параметры для этого оценщика и вложенных подобъектов, которые являются оценщиками.
- Возвращает:
- paramsdict
Имена параметров, сопоставленные с их значениями.
- свойство гиперпараметры#
Возвращает список всех спецификаций гиперпараметров.
- is_stationary()[источник]#
Возвращает, является ли ядро стационарным.
- свойство n_dims#
Возвращает количество нефиксированных гиперпараметров ядра.
- свойство requires_vector_input#
Возвращает, определено ли ядро на векторах признаков фиксированной длины или на общих объектах. По умолчанию True для обратной совместимости.
- set_params(**params)[источник]#
Установите параметры этого ядра.
Метод работает как на простых ядрах, так и на вложенных ядрах. Последние имеют параметры вида
__ - Возвращает:
- self
- свойство theta#
Возвращает (сглаженные, логарифмически преобразованные) нефиксированные гиперпараметры.
Обратите внимание, что theta обычно являются логарифмически преобразованными значениями гиперпараметров ядра, так как это представление пространства поиска более подходит для поиска гиперпараметров, поскольку гиперпараметры, такие как масштабы длины, естественно существуют в логарифмическом масштабе.
- Возвращает:
- thetandarray формы (n_dims,)
Нефиксированные, логарифмически преобразованные гиперпараметры ядра
Примеры галереи#
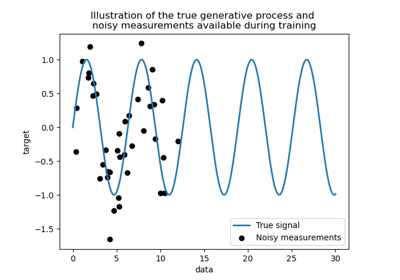
Сравнение ядерной гребневой регрессии и регрессии по методу Гауссовских процессов
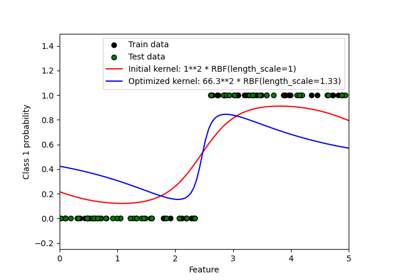
Вероятностные предсказания с гауссовским процессом классификации (GPC)
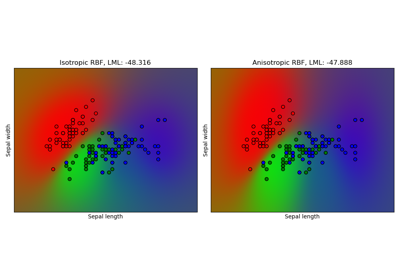
Гауссовский процесс классификации (GPC) на наборе данных iris
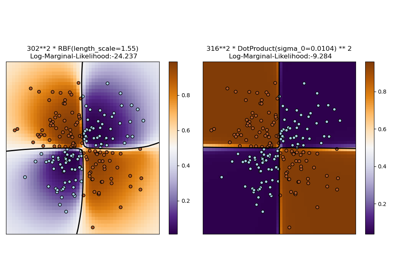
Иллюстрация классификации гауссовским процессом (GPC) на наборе данных XOR
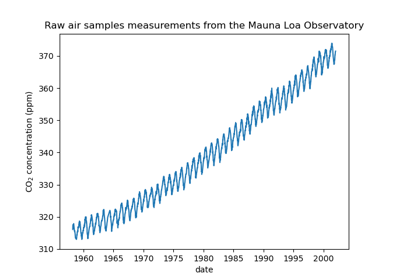
Прогнозирование уровня CO2 на наборе данных Mona Loa с использованием гауссовской регрессии (GPR)
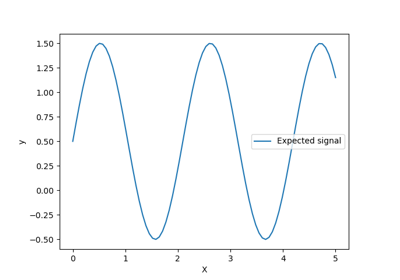
Способность гауссовского процесса регрессии (GPR) оценивать уровень шума данных
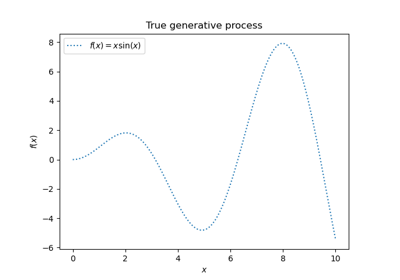
Регрессия гауссовских процессов: базовый вводный пример
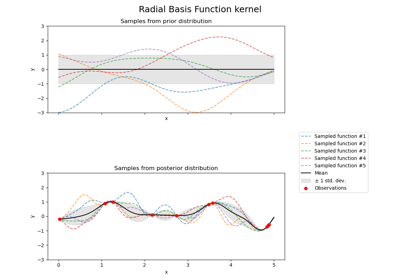
Иллюстрация априорного и апостериорного гауссовских процессов для различных ядер