Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Способность гауссовского процесса регрессии (GPR) оценивать уровень шума данных#
Этот пример демонстрирует способность
WhiteKernel для оценки уровня шума в данных. Кроме того, мы показываем важность инициализации гиперпараметров ядра.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Генерация данных#
Мы будем работать в условиях, где X будет содержать один признак. Мы создаём
функцию, которая будет генерировать целевую переменную для предсказания. Мы добавим
опцию для добавления некоторого шума к сгенерированной целевой переменной.
import numpy as np
def target_generator(X, add_noise=False):
target = 0.5 + np.sin(3 * X)
if add_noise:
rng = np.random.RandomState(1)
target += rng.normal(0, 0.3, size=target.shape)
return target.squeeze()
Давайте посмотрим на генератор целевых значений, где мы не будем добавлять шум, чтобы наблюдать сигнал, который мы хотели бы предсказать.
X = np.linspace(0, 5, num=80).reshape(-1, 1)
y = target_generator(X, add_noise=False)
import matplotlib.pyplot as plt
plt.plot(X, y, label="Expected signal")
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")
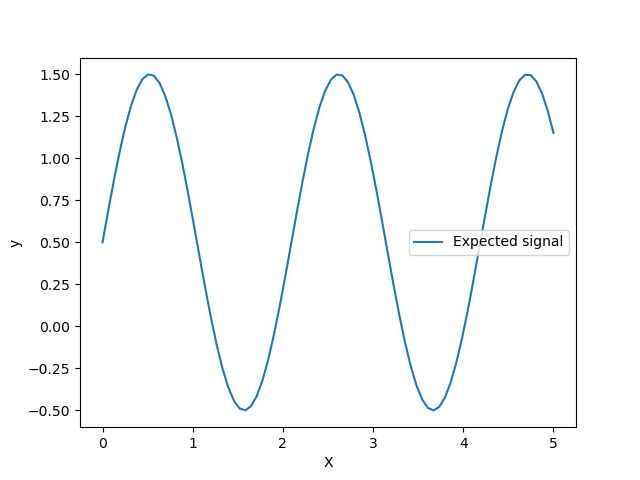
Цель - преобразование входных данных X используя синусоидальную функцию. Теперь мы сгенерируем несколько зашумленных обучающих выборок. Чтобы проиллюстрировать уровень шума, мы построим график истинного сигнала вместе с зашумленными обучающими выборками.
rng = np.random.RandomState(0)
X_train = rng.uniform(0, 5, size=20).reshape(-1, 1)
y_train = target_generator(X_train, add_noise=True)
plt.plot(X, y, label="Expected signal")
plt.scatter(
x=X_train[:, 0],
y=y_train,
color="black",
alpha=0.4,
label="Observations",
)
plt.legend()
plt.xlabel("X")
_ = plt.ylabel("y")
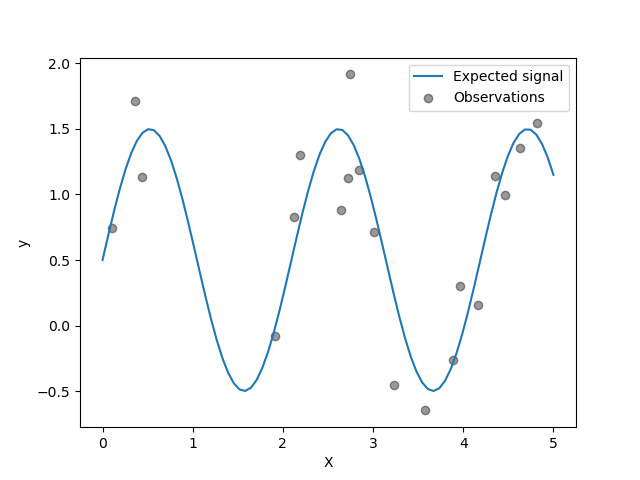
Оптимизация гиперпараметров ядра в GPR#
Теперь мы создадим
GaussianProcessRegressor
используя аддитивное ядро, добавляющее
RBF и
WhiteKernel ядра.
WhiteKernel является ядром, которое
сможет оценить количество шума, присутствующего в данных, в то время как
RBF будет служить для подгонки нелинейности между данными и целевой переменной.
Однако мы покажем, что пространство гиперпараметров содержит несколько локальных минимумов. Это подчеркнет важность начальных значений гиперпараметров.
Мы создадим модель, используя ядро с высоким уровнем шума и большим масштабом длины, которая объяснит все вариации в данных шумом.
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF, WhiteKernel
kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
/home/circleci/project/sklearn/gaussian_process/kernels.py:450: ConvergenceWarning:
The optimal value found for dimension 0 of parameter k1__k2__length_scale is close to the specified upper bound 1000.0. Increasing the bound and calling fit again may find a better value.
plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
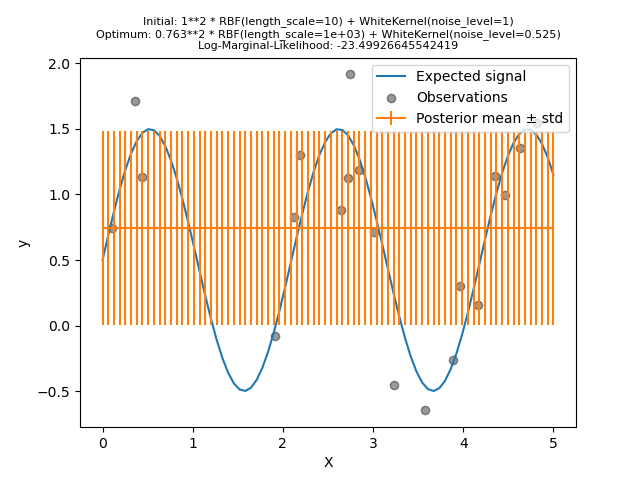
Мы видим, что найденное оптимальное ядро всё ещё имеет высокий уровень шума и даже большую длину масштаба. Длина масштаба достигает максимальной границы, которую мы допустили для этого параметра, и в результате мы получили предупреждение.
Что более важно, мы наблюдаем, что модель не дает полезных прогнозов: средний прогноз, кажется, постоянен: он не следует ожидаемому сигналу без шума.
Теперь мы инициализируем RBF
с большим length_scale начальное значение и
WhiteKernel с меньшим начальным
уровнем шума, сохраняя границы параметров неизменными.
kernel = 1.0 * RBF(length_scale=1e-1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1e-2, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0.0)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
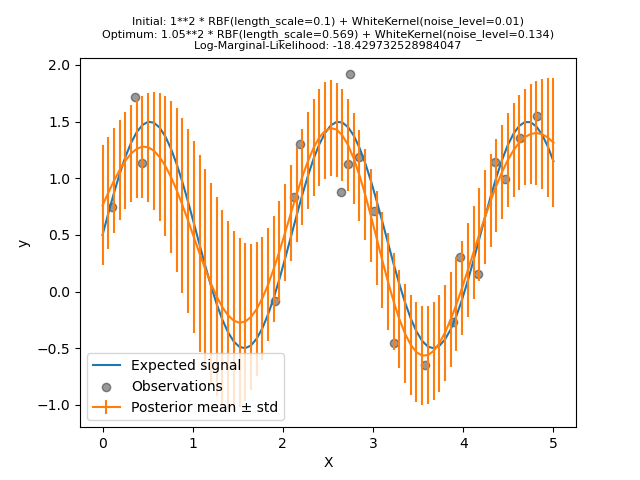
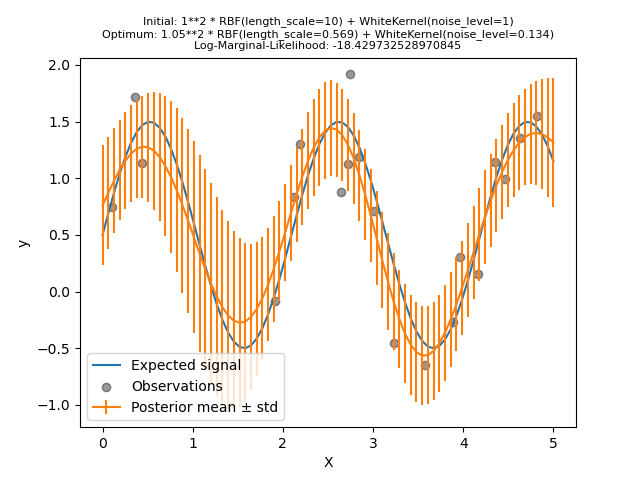
Во-первых, мы видим, что предсказания модели более точны, чем у предыдущей модели: эта новая модель способна оценить функциональную зависимость без шума.
Глядя на гиперпараметры ядра, мы видим, что наилучшая найденная комбинация имеет меньший уровень шума и более короткий масштаб длины, чем первая модель.
Мы можем проверить отрицательное логарифмическое маргинальное правдоподобие (LML) для
GaussianProcessRegressor
для различных гиперпараметров, чтобы получить представление о локальных минимумах.
from matplotlib.colors import LogNorm
length_scale = np.logspace(-2, 4, num=80)
noise_level = np.logspace(-2, 1, num=80)
length_scale_grid, noise_level_grid = np.meshgrid(length_scale, noise_level)
log_marginal_likelihood = [
gpr.log_marginal_likelihood(theta=np.log([0.36, scale, noise]))
for scale, noise in zip(length_scale_grid.ravel(), noise_level_grid.ravel())
]
log_marginal_likelihood = np.reshape(log_marginal_likelihood, noise_level_grid.shape)
vmin, vmax = (-log_marginal_likelihood).min(), 50
level = np.around(np.logspace(np.log10(vmin), np.log10(vmax), num=20), decimals=1)
plt.contour(
length_scale_grid,
noise_level_grid,
-log_marginal_likelihood,
levels=level,
norm=LogNorm(vmin=vmin, vmax=vmax),
)
plt.colorbar()
plt.xscale("log")
plt.yscale("log")
plt.xlabel("Length-scale")
plt.ylabel("Noise-level")
plt.title("Negative log-marginal-likelihood")
plt.show()
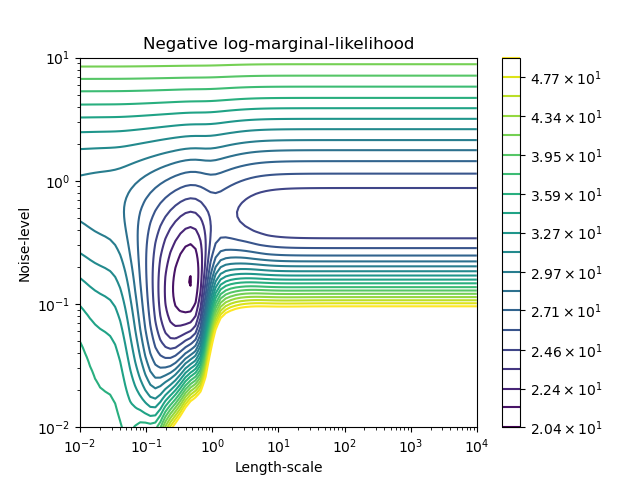
Мы видим, что есть два локальных минимума, соответствующих комбинации гиперпараметров, найденной ранее. В зависимости от начальных значений гиперпараметров градиентная оптимизация может сходиться или не сходиться к лучшей модели. Поэтому важно повторять оптимизацию несколько раз с разными инициализациями. Это можно сделать, установив
n_restarts_optimizer параметр
GaussianProcessRegressor класс.
Попробуем снова обучить нашу модель с плохими начальными значениями, но на этот раз с 10 случайными перезапусками.
kernel = 1.0 * RBF(length_scale=1e1, length_scale_bounds=(1e-2, 1e3)) + WhiteKernel(
noise_level=1, noise_level_bounds=(1e-10, 1e1)
)
gpr = GaussianProcessRegressor(
kernel=kernel, alpha=0.0, n_restarts_optimizer=10, random_state=0
)
gpr.fit(X_train, y_train)
y_mean, y_std = gpr.predict(X, return_std=True)
plt.plot(X, y, label="Expected signal")
plt.scatter(x=X_train[:, 0], y=y_train, color="black", alpha=0.4, label="Observations")
plt.errorbar(X, y_mean, y_std, label="Posterior mean ± std")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
_ = plt.title(
(
f"Initial: {kernel}\nOptimum: {gpr.kernel_}\nLog-Marginal-Likelihood: "
f"{gpr.log_marginal_likelihood(gpr.kernel_.theta)}"
),
fontsize=8,
)
Как мы и надеялись, случайные перезапуски позволяют оптимизации найти лучший набор гиперпараметров, несмотря на плохие начальные значения.
Общее время выполнения скрипта: (0 минут 5.724 секунд)
Связанные примеры
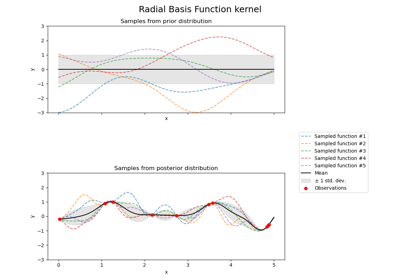
Иллюстрация априорного и апостериорного гауссовских процессов для различных ядер
Регрессия гауссовских процессов: базовый вводный пример
Вероятностные предсказания с гауссовским процессом классификации (GPC)
Прогнозирование уровня CO2 на наборе данных Mona Loa с использованием гауссовской регрессии (GPR)