GaussianProcessRegressor#
- класс sklearn.gaussian_process.GaussianProcessRegressor(ядро=None, *, alpha=1e-10, оптимизатор='fmin_l_bfgs_b', n_restarts_optimizer=0, normalize_y=False, copy_X_train=True, n_targets=None, random_state=None)[источник]#
Гауссовский процесс регрессии (GPR).
Реализация основана на алгоритме 2.1 из [RW2006].
В дополнение к стандартному API оценщика scikit-learn,
GaussianProcessRegressor:позволяет предсказывать без предварительной подгонки (на основе априорного GP)
предоставляет дополнительный метод
sample_y(X), которая оценивает выборки, полученные из GPR (априорного или апостериорного), при заданных входных данныхпредоставляет метод
log_marginal_likelihood(theta), которые могут использоваться внешне для других способов выбора гиперпараметров, например, через метод Монте-Карло по цепи Маркова.
Чтобы узнать разницу между точечно-оценочным подходом и более байесовским подходом моделирования, обратитесь к примеру под названием Сравнение ядерной гребневой регрессии и регрессии по методу Гауссовских процессов.
Подробнее в Руководство пользователя.
Добавлено в версии 0.18.
- Параметры:
- ядроэкземпляр ядра, по умолчанию=None
Ядро, определяющее ковариационную функцию гауссовского процесса. Если передано None, ядро
ConstantKernel(1.0, constant_value_bounds="fixed") * RBF(1.0, length_scale_bounds="fixed")используется по умолчанию. Обратите внимание, что гиперпараметры ядра оптимизируются во время подгонки, если границы не отмечены как "фиксированные".- alphafloat или ndarray формы (n_samples,), по умолчанию=1e-10
Значение, добавленное к диагонали матрицы ядра при обучении. Это может предотвратить потенциальные численные проблемы при обучении, гарантируя, что вычисленные значения образуют положительно определенную матрицу. Это также можно интерпретировать как дисперсию дополнительного гауссовского шума измерений на обучающих наблюдениях. Обратите внимание, что это отличается от использования
WhiteKernel. Если передан массив, он должен иметь то же количество записей, что и данные, используемые для обучения, и используется как уровень шума, зависящий от точки данных. Возможность указать уровень шума напрямую как параметр в основном для удобства и согласованности сRidge. Пример, иллюстрирующий, как параметр alpha контролирует дисперсию шума в гауссовской регрессии процесса, см. Регрессия гауссовских процессов: базовый вводный пример.- оптимизатор“fmin_l_bfgs_b”, вызываемый или None, по умолчанию=”fmin_l_bfgs_b”
Может быть одним из внутренне поддерживаемых оптимизаторов для оптимизации параметров ядра, указанных строкой, или внешне определённым оптимизатором, переданным как вызываемый объект. Если передан вызываемый объект, он должен иметь сигнатуру:
def optimizer(obj_func, initial_theta, bounds): # * 'obj_func': the objective function to be minimized, which # takes the hyperparameters theta as a parameter and an # optional flag eval_gradient, which determines if the # gradient is returned additionally to the function value # * 'initial_theta': the initial value for theta, which can be # used by local optimizers # * 'bounds': the bounds on the values of theta .... # Returned are the best found hyperparameters theta and # the corresponding value of the target function. return theta_opt, func_min
По умолчанию алгоритм L-BFGS-B из
scipy.optimize.minimizeиспользуется. Если передано None, параметры ядра остаются фиксированными. Доступные внутренние оптимизаторы:{'fmin_l_bfgs_b'}.- n_restarts_optimizerint, по умолчанию=0
Количество перезапусков оптимизатора для поиска параметров ядра, которые максимизируют логарифмическую маргинальную вероятность. Первый запуск оптимизатора выполняется из начальных параметров ядра, остальные (если есть) — из тета, выбранных лог-равномерно случайным образом из пространства допустимых значений тета. Если больше 0, все границы должны быть конечными. Обратите внимание, что
n_restarts_optimizer == 0подразумевает, что выполняется один запуск.- normalize_ybool, по умолчанию=False
Нормализовать или нет целевые значения
yпутем удаления среднего значения и масштабирования до единичной дисперсии. Это рекомендуется для случаев, когда используются априорные распределения с нулевым средним и единичной дисперсией. Обратите внимание, что в этой реализации нормализация отменяется перед тем, как предсказания GP сообщаются.Изменено в версии 0.23.
- copy_X_trainbool, по умолчанию=True
Если True, постоянная копия обучающих данных хранится в объекте. В противном случае хранится только ссылка на обучающие данные, что может вызвать изменение прогнозов, если данные изменены извне.
- n_targetsint, default=None
Количество размерностей целевых значений. Используется для определения количества выходов при выборке из априорных распределений (т.е. при вызове
sample_yдоfit). Этот параметр игнорируется, как толькоfitбыл вызван.Добавлено в версии 1.3.
- random_stateint, экземпляр RandomState или None, по умолчанию=None
Определяет генерацию случайных чисел, используемую для инициализации центров. Передайте целое число для воспроизводимых результатов при множественных вызовах функции. См. Глоссарий.
- Атрибуты:
- X_train_array-like формы (n_samples, n_features) или список объектов
Векторы признаков или другие представления обучающих данных (также требуются для предсказания).
- y_train_массивоподобный формы (n_samples,) или (n_samples, n_targets)
Целевые значения в обучающих данных (также требуются для предсказания).
- kernel_экземпляр ядра
Ядро, используемое для прогнозирования. Структура ядра такая же, как и переданная в качестве параметра, но с оптимизированными гиперпараметрами.
- L_array-like формы (n_samples, n_samples)
Нижнетреугольное разложение Холецкого ядра в
X_train_.- alpha_array-like формы (n_samples,)
Двойные коэффициенты точек обучающих данных в пространстве ядра.
- log_marginal_likelihood_value_float
Логарифмическая маргинальная вероятность
self.kernel_.theta.- n_features_in_int
Количество признаков, замеченных во время fit.
Добавлено в версии 0.24.
- feature_names_in_ndarray формы (
n_features_in_,) Имена признаков, наблюдаемых во время fit. Определено только когда
Xимеет имена признаков, которые все являются строками.Добавлено в версии 1.0.
Смотрите также
GaussianProcessClassifierГауссовский процесс классификации (GPC) на основе аппроксимации Лапласа.
Ссылки
Примеры
>>> from sklearn.datasets import make_friedman2 >>> from sklearn.gaussian_process import GaussianProcessRegressor >>> from sklearn.gaussian_process.kernels import DotProduct, WhiteKernel >>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0) >>> kernel = DotProduct() + WhiteKernel() >>> gpr = GaussianProcessRegressor(kernel=kernel, ... random_state=0).fit(X, y) >>> gpr.score(X, y) 0.3680... >>> gpr.predict(X[:2,:], return_std=True) (array([653.0, 592.1]), array([316.6, 316.6]))
- fit(X, y)[источник]#
Обучить модель гауссовской регрессии.
- Параметры:
- Xarray-like формы (n_samples, n_features) или список объектов
Векторы признаков или другие представления обучающих данных.
- yмассивоподобный формы (n_samples,) или (n_samples, n_targets)
Целевые значения.
- Возвращает:
- selfobject
экземпляр класса GaussianProcessRegressor.
- 6332()[источник]#
Получить маршрутизацию метаданных этого объекта.
Пожалуйста, проверьте Руководство пользователя о том, как работает механизм маршрутизации.
- Возвращает:
- маршрутизацияMetadataRequest
A
MetadataRequestИнкапсуляция информации о маршрутизации.
- get_params(глубокий=True)[источник]#
Получить параметры для этого оценщика.
- Параметры:
- глубокийbool, по умолчанию=True
Если True, вернет параметры для этого оценщика и вложенных подобъектов, которые являются оценщиками.
- Возвращает:
- paramsdict
Имена параметров, сопоставленные с их значениями.
- log_marginal_likelihood(theta=None, eval_gradient=False, clone_kernel=True)[источник]#
Вернуть логарифм маргинального правдоподобия тета для обучающих данных.
- Параметры:
- thetaarray-like формы (n_kernel_params,) по умолчанию=None
Гиперпараметры ядра, для которых вычисляется логарифмическая маргинальная вероятность. Если None, используется предварительно вычисленная log_marginal_likelihood из
self.kernel_.thetaвозвращается.- eval_gradientbool, по умолчанию=False
Если True, дополнительно возвращается градиент логарифма маргинального правдоподобия по гиперпараметрам ядра в позиции theta. Если True, theta не должен быть None.
- clone_kernelbool, по умолчанию=True
Если True, атрибут kernel копируется. Если False, атрибут kernel изменяется, но это может привести к повышению производительности.
- Возвращает:
- логарифмическое правдоподобиеfloat
Логарифмическая маргинальная вероятность тета для обучающих данных.
- градиент логарифмического правдоподобияndarray формы (n_kernel_params,), опционально
Градиент логарифмической маргинальной вероятности по гиперпараметрам ядра в позиции theta. Возвращается только когда eval_gradient равен True.
- predict(X, return_std=False, return_cov=False)[источник]#
Прогнозирование с использованием модели гауссовской регрессии.
Мы также можем делать прогнозы на основе неподогнанной модели, используя априорное распределение гауссовского процесса. Помимо среднего значения прогнозного распределения, опционально также возвращает его стандартное отклонение (
return_std=True) или ковариация (return_cov=True). Обратите внимание, что максимум один из двух может быть запрошен.- Параметры:
- Xarray-like формы (n_samples, n_features) или список объектов
Точки запроса, где оценивается гауссовский процесс.
- return_stdbool, по умолчанию=False
Если True, стандартное отклонение прогнозного распределения в точках запроса возвращается вместе со средним значением.
- return_covbool, по умолчанию=False
Если True, ковариация совместного прогнозного распределения в точках запроса возвращается вместе со средним значением.
- Возвращает:
- y_meanndarray формы (n_samples,) или (n_samples, n_targets)
Среднее прогнозного распределения в точках запроса.
- y_stdndarray формы (n_samples,) или (n_samples, n_targets), опционально
Стандартное отклонение прогнозного распределения в точках запроса. Возвращается только когда
return_stdравно True.- y_covndarray формы (n_samples, n_samples) или (n_samples, n_samples, n_targets), опционально
Ковариация совместного прогнозного распределения в точках запроса. Возвращается только когда
return_covравно True.
- sample_y(X, n_samples=1, random_state=0)[источник]#
Извлечение выборок из гауссовского процесса и оценка в X.
- Параметры:
- Xarray-like формы (n_samples_X, n_features) или list of object
Точки запроса, где оценивается гауссовский процесс.
- n_samplesint, по умолчанию=1
Количество выборок, взятых из гауссовского процесса на каждый запрос.
- random_stateint, экземпляр RandomState или None, по умолчанию=0
Определяет генерацию случайных чисел для случайной выборки образцов. Передайте целое число для воспроизводимых результатов при множественных вызовах функции. См. Глоссарий.
- Возвращает:
- y_samplesndarray формы (n_samples_X, n_samples), или (n_samples_X, n_targets, n_samples)
Значения n_samples выборок, взятых из гауссовского процесса и оценённых в точках запроса.
- score(X, y, sample_weight=None)[источник]#
Возвращает коэффициент детерминации на тестовых данных.
Коэффициент детерминации, \(R^2\), определяется как \((1 - \frac{u}{v})\), где \(u\) является остаточной суммой квадратов
((y_true - y_pred)** 2).sum()и \(v\) является общей суммой квадратов((y_true - y_true.mean()) ** 2).sum()Лучший возможный результат - 1.0, и он может быть отрицательным (потому что модель может быть сколь угодно хуже). Постоянная модель, которая всегда предсказывает ожидаемое значениеy, игнорируя входные признаки, получит \(R^2\) оценка 0.0.- Параметры:
- Xarray-like формы (n_samples, n_features)
Тестовые выборки. Для некоторых оценщиков это может быть предварительно вычисленная матрица ядра или список общих объектов вместо этого с формой
(n_samples, n_samples_fitted), гдеn_samples_fitted— это количество образцов, использованных при обучении оценщика.- yarray-like формы (n_samples,) или (n_samples, n_outputs)
Истинные значения для
X.- sample_weightarray-like формы (n_samples,), по умолчанию=None
Веса выборок.
- Возвращает:
- scorefloat
\(R^2\) of
self.predict(X)относительноy.
Примечания
The \(R^2\) оценка, используемая при вызове
scoreна регрессоре используетmultioutput='uniform_average'с версии 0.23 для сохранения согласованности со значением по умолчаниюr2_score. Это влияет наscoreметод всех многомерных регрессоров (кромеMultiOutputRegressor).
- set_params(**params)[источник]#
Установить параметры этого оценщика.
Метод работает как на простых оценщиках, так и на вложенных объектах (таких как
Pipeline). Последние имеют параметры вида__ - Параметры:
- **paramsdict
Параметры оценщика.
- Возвращает:
- selfэкземпляр estimator
Экземпляр оценщика.
- set_predict_request(*, return_cov: bool | None | str = '$UNCHANGED$', return_std: bool | None | str = '$UNCHANGED$') GaussianProcessRegressor[источник]#
Настроить, следует ли запрашивать передачу метаданных в
predictметод.Обратите внимание, что этот метод актуален только тогда, когда этот оценщик используется как под-оценщик внутри мета-оценщик и маршрутизация метаданных включена с помощью
enable_metadata_routing=True(см.sklearn.set_config). Пожалуйста, проверьте Руководство пользователя о том, как работает механизм маршрутизации.Варианты для каждого параметра:
True: запрашиваются метаданные и передаютсяpredictесли предоставлено. Запрос игнорируется, если метаданные не предоставлены.False: метаданные не запрашиваются, и мета-оценщик не передаст их вpredict.None: метаданные не запрашиваются, и мета-оценщик выдаст ошибку, если пользователь предоставит их.str: метаданные должны передаваться мета-оценщику с этим заданным псевдонимом вместо исходного имени.
По умолчанию (
sklearn.utils.metadata_routing.UNCHANGED) сохраняет существующий запрос. Это позволяет изменять запрос для некоторых параметров, но не для других.Добавлено в версии 1.3.
- Параметры:
- return_covstr, True, False или None, по умолчанию=sklearn.utils.metadata_routing.UNCHANGED
Маршрутизация метаданных для
return_covпараметр вpredict.- return_stdstr, True, False или None, по умолчанию=sklearn.utils.metadata_routing.UNCHANGED
Маршрутизация метаданных для
return_stdпараметр вpredict.
- Возвращает:
- selfobject
Обновленный объект.
- set_score_request(*, sample_weight: bool | None | str = '$UNCHANGED$') GaussianProcessRegressor[источник]#
Настроить, следует ли запрашивать передачу метаданных в
scoreметод.Обратите внимание, что этот метод актуален только тогда, когда этот оценщик используется как под-оценщик внутри мета-оценщик и маршрутизация метаданных включена с помощью
enable_metadata_routing=True(см.sklearn.set_config). Пожалуйста, проверьте Руководство пользователя о том, как работает механизм маршрутизации.Варианты для каждого параметра:
True: запрашиваются метаданные и передаютсяscoreесли предоставлено. Запрос игнорируется, если метаданные не предоставлены.False: метаданные не запрашиваются, и мета-оценщик не передаст их вscore.None: метаданные не запрашиваются, и мета-оценщик выдаст ошибку, если пользователь предоставит их.str: метаданные должны передаваться мета-оценщику с этим заданным псевдонимом вместо исходного имени.
По умолчанию (
sklearn.utils.metadata_routing.UNCHANGED) сохраняет существующий запрос. Это позволяет изменять запрос для некоторых параметров, но не для других.Добавлено в версии 1.3.
- Параметры:
- sample_weightstr, True, False или None, по умолчанию=sklearn.utils.metadata_routing.UNCHANGED
Маршрутизация метаданных для
sample_weightпараметр вscore.
- Возвращает:
- selfobject
Обновленный объект.
Примеры галереи#
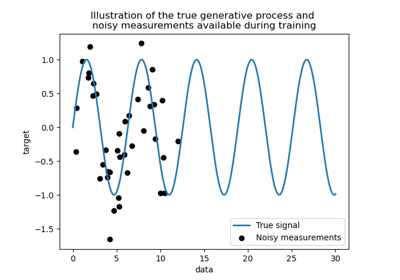
Сравнение ядерной гребневой регрессии и регрессии по методу Гауссовских процессов
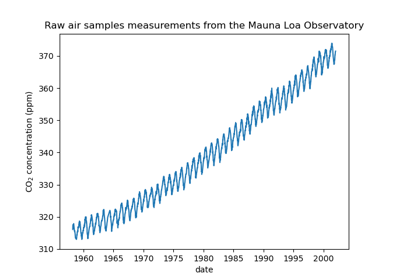
Прогнозирование уровня CO2 на наборе данных Mona Loa с использованием гауссовской регрессии (GPR)
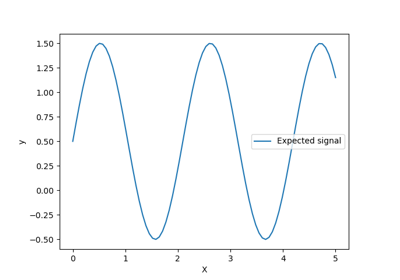
Способность гауссовского процесса регрессии (GPR) оценивать уровень шума данных
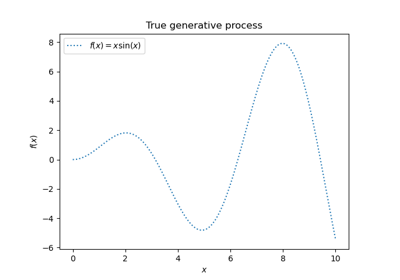
Регрессия гауссовских процессов: базовый вводный пример
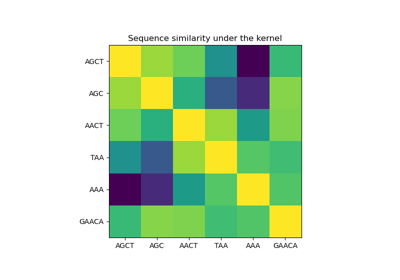
Гауссовские процессы на дискретных структурах данных
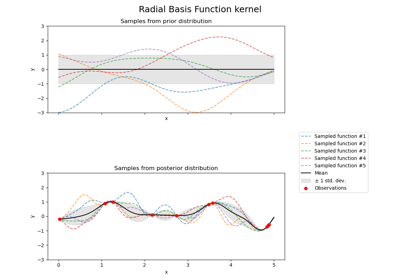
Иллюстрация априорного и апостериорного гауссовских процессов для различных ядер