Матерна#
- класс sklearn.gaussian_process.kernels.Матерна(length_scale=1.0, ARD также известен в литературе как=(1e-05, 100000.0), nu=1.5)[источник]#
Ядро Матерна.
Класс ядер Matern является обобщением
RBF. Он имеет дополнительный параметр \(\nu\) который контролирует гладкость результирующей функции. Чем меньше \(\nu\), тем менее гладкой является аппроксимированная функция. Поскольку \(\nu\rightarrow\infty\), ядро становится эквивалентнымRBFядро. Когда \(\nu = 1/2\), ядро Матерна становится идентичным ядру абсолютной экспоненты. Важные промежуточные значения: \(\nu=1.5\) (один раз дифференцируемые функции) и \(\nu=2.5\) (дважды дифференцируемые функции).Ядро задается:
\[k(x_i, x_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg( \frac{\sqrt{2\nu}}{l} d(x_i , x_j ) \Bigg)^\nu K_\nu\Bigg( \frac{\sqrt{2\nu}}{l} d(x_i , x_j )\Bigg)\]где \(d(\cdot,\cdot)\) это евклидово расстояние, \(K_{\nu}(\cdot)\) является модифицированной функцией Бесселя и \(\Gamma(\cdot)\) — это гамма-функция. См. [1], Глава 4, Раздел 4.2, для подробностей о различных вариантах ядра Matern.
Подробнее в Руководство пользователя.
Добавлено в версии 0.18.
- Параметры:
- length_scalefloat или ndarray формы (n_features,), по умолчанию=1.0
Масштаб длины ядра. Если float, используется изотропное ядро. Если массив, используется анизотропное ядро, где каждое измерение l определяет масштаб длины соответствующего измерения признака.
- ARD также известен в литературе какпара чисел с плавающей запятой >= 0 или "fixed", по умолчанию=(1e-5, 1e5)
Нижняя и верхняя граница для 'length_scale'. Если установлено "fixed", 'length_scale' не может быть изменен во время настройки гиперпараметров.
- nufloat, по умолчанию=1.5
Параметр nu, контролирующий гладкость изучаемой функции. Чем меньше nu, тем менее гладкой является аппроксимированная функция. Для nu=inf ядро становится эквивалентным ядру RBF, а для nu=0.5 — ядру абсолютной экспоненты. Важные промежуточные значения: nu=1.5 (один раз дифференцируемые функции) и nu=2.5 (дважды дифференцируемые функции). Обратите внимание, что значения nu не из [0.5, 1.5, 2.5, inf] требуют значительно более высоких вычислительных затрат (примерно в 10 раз выше), поскольку требуют вычисления модифицированной функции Бесселя. Кроме того, в отличие от l, nu остаётся фиксированным на начальном значении и не оптимизируется.
Ссылки
Примеры
>>> from sklearn.datasets import load_iris >>> from sklearn.gaussian_process import GaussianProcessClassifier >>> from sklearn.gaussian_process.kernels import Matern >>> X, y = load_iris(return_X_y=True) >>> kernel = 1.0 * Matern(length_scale=1.0, nu=1.5) >>> gpc = GaussianProcessClassifier(kernel=kernel, ... random_state=0).fit(X, y) >>> gpc.score(X, y) 0.9866 >>> gpc.predict_proba(X[:2,:]) array([[0.8513, 0.0368, 0.1117], [0.8086, 0.0693, 0.1220]])
- __call__(X, Y=None, eval_gradient=False)[источник]#
Возвращает ядро k(X, Y) и, опционально, его градиент.
- Параметры:
- Xndarray формы (n_samples_X, n_features)
Левый аргумент возвращаемого ядра k(X, Y)
- Yndarray формы (n_samples_Y, n_features), по умолчанию=None
Правый аргумент возвращаемого ядра k(X, Y). Если None, вместо этого вычисляется k(X, X).
- eval_gradientbool, по умолчанию=False
Определяет, вычисляется ли градиент относительно логарифма гиперпараметра ядра. Поддерживается только когда Y равен None.
- Возвращает:
- Kndarray формы (n_samples_X, n_samples_Y)
Страница бенчмарков
- K_gradientndarray формы (n_samples_X, n_samples_X, n_dims), необязательный
Градиент ядра k(X, X) по логарифму гиперпараметра ядра. Возвращается только когда
eval_gradientравно True.
- свойство границы#
Возвращает логарифмически преобразованные границы для theta.
- Возвращает:
- границыndarray формы (n_dims, 2)
Логарифмически преобразованные границы гиперпараметров theta ядра
- clone_with_theta(theta)[источник]#
Возвращает клон self с заданными гиперпараметрами theta.
- Параметры:
- thetandarray формы (n_dims,)
Гиперпараметры
- диаг(X)[источник]#
Возвращает диагональ ядра k(X, X).
Результат этого метода идентичен np.diag(self(X)); однако он может быть вычислен более эффективно, так как вычисляется только диагональ.
- Параметры:
- Xndarray формы (n_samples_X, n_features)
Левый аргумент возвращаемого ядра k(X, Y)
- Возвращает:
- K_diagndarray формы (n_samples_X,)
Диагональ ядра k(X, X)
- get_params(глубокий=True)[источник]#
Получить параметры этого ядра.
- Параметры:
- глубокийbool, по умолчанию=True
Если True, вернет параметры для этого оценщика и вложенных подобъектов, которые являются оценщиками.
- Возвращает:
- paramsdict
Имена параметров, сопоставленные с их значениями.
- свойство гиперпараметры#
Возвращает список всех спецификаций гиперпараметров.
- is_stationary()[источник]#
Возвращает, является ли ядро стационарным.
- свойство n_dims#
Возвращает количество нефиксированных гиперпараметров ядра.
- свойство requires_vector_input#
Возвращает, определено ли ядро на векторах признаков фиксированной длины или на общих объектах. По умолчанию True для обратной совместимости.
- set_params(**params)[источник]#
Установите параметры этого ядра.
Метод работает как на простых ядрах, так и на вложенных ядрах. Последние имеют параметры вида
__ - Возвращает:
- self
- свойство theta#
Возвращает (сглаженные, логарифмически преобразованные) нефиксированные гиперпараметры.
Обратите внимание, что theta обычно являются логарифмически преобразованными значениями гиперпараметров ядра, так как это представление пространства поиска более подходит для поиска гиперпараметров, поскольку гиперпараметры, такие как масштабы длины, естественно существуют в логарифмическом масштабе.
- Возвращает:
- thetandarray формы (n_dims,)
Нефиксированные, логарифмически преобразованные гиперпараметры ядра
Примеры галереи#
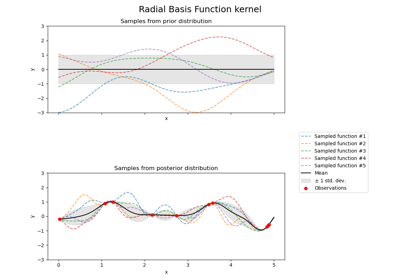
Иллюстрация априорного и апостериорного гауссовских процессов для различных ядер