Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Вероятностные предсказания с гауссовским процессом классификации (GPC)#
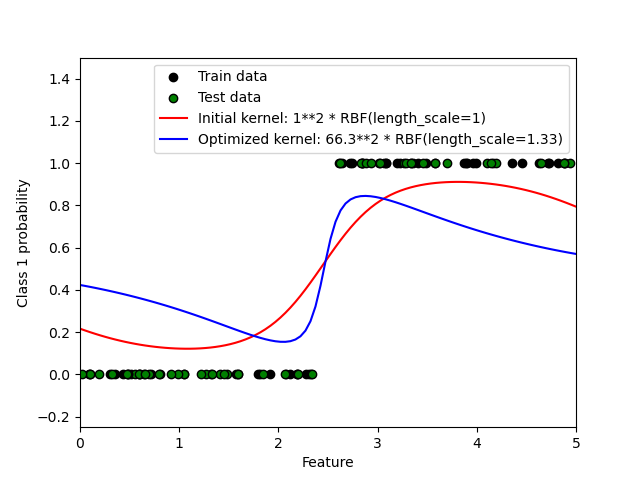
Этот пример иллюстрирует предсказанную вероятность GPC для RBF ядра с различными вариантами гиперпараметров. Первый рисунок показывает предсказанную вероятность GPC с произвольно выбранными гиперпараметрами и с гиперпараметрами, соответствующими максимальному логарифмическому маргинальному правдоподобию (LML).
Хотя гиперпараметры, выбранные путем оптимизации LML, имеют значительно больший LML, они работают немного хуже согласно логарифмическим потерям на тестовых данных. На рисунке видно, что это происходит потому, что они демонстрируют резкое изменение вероятностей классов на границах классов (что хорошо), но имеют предсказанные вероятности близкие к 0.5 далеко от границ классов (что плохо). Этот нежелательный эффект вызван приближением Лапласа, используемым внутренне GPC.
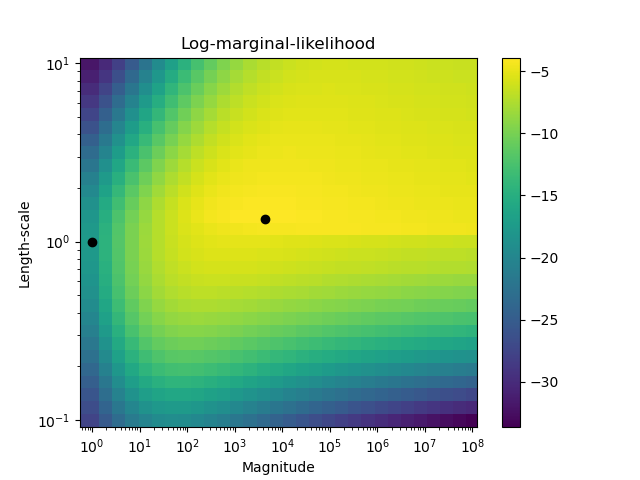
Второй рисунок показывает логарифмическую маргинальную вероятность для различных вариантов гиперпараметров ядра, выделяя два выбора гиперпараметров, использованных на первом рисунке, черными точками.
Log Marginal Likelihood (initial): -17.598
Log Marginal Likelihood (optimized): -3.875
Accuracy: 1.000 (initial) 1.000 (optimized)
Log-loss: 0.214 (initial) 0.319 (optimized)
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import numpy as np
from matplotlib import pyplot as plt
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import accuracy_score, log_loss
# Generate data
train_size = 50
rng = np.random.RandomState(0)
X = rng.uniform(0, 5, 100)[:, np.newaxis]
y = np.array(X[:, 0] > 2.5, dtype=int)
# Specify Gaussian Processes with fixed and optimized hyperparameters
gp_fix = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0), optimizer=None)
gp_fix.fit(X[:train_size], y[:train_size])
gp_opt = GaussianProcessClassifier(kernel=1.0 * RBF(length_scale=1.0))
gp_opt.fit(X[:train_size], y[:train_size])
print(
"Log Marginal Likelihood (initial): %.3f"
% gp_fix.log_marginal_likelihood(gp_fix.kernel_.theta)
)
print(
"Log Marginal Likelihood (optimized): %.3f"
% gp_opt.log_marginal_likelihood(gp_opt.kernel_.theta)
)
print(
"Accuracy: %.3f (initial) %.3f (optimized)"
% (
accuracy_score(y[:train_size], gp_fix.predict(X[:train_size])),
accuracy_score(y[:train_size], gp_opt.predict(X[:train_size])),
)
)
print(
"Log-loss: %.3f (initial) %.3f (optimized)"
% (
log_loss(y[:train_size], gp_fix.predict_proba(X[:train_size])[:, 1]),
log_loss(y[:train_size], gp_opt.predict_proba(X[:train_size])[:, 1]),
)
)
# Plot posteriors
plt.figure()
plt.scatter(
X[:train_size, 0], y[:train_size], c="k", label="Train data", edgecolors=(0, 0, 0)
)
plt.scatter(
X[train_size:, 0], y[train_size:], c="g", label="Test data", edgecolors=(0, 0, 0)
)
X_ = np.linspace(0, 5, 100)
plt.plot(
X_,
gp_fix.predict_proba(X_[:, np.newaxis])[:, 1],
"r",
label="Initial kernel: %s" % gp_fix.kernel_,
)
plt.plot(
X_,
gp_opt.predict_proba(X_[:, np.newaxis])[:, 1],
"b",
label="Optimized kernel: %s" % gp_opt.kernel_,
)
plt.xlabel("Feature")
plt.ylabel("Class 1 probability")
plt.xlim(0, 5)
plt.ylim(-0.25, 1.5)
plt.legend(loc="best")
# Plot LML landscape
plt.figure()
theta0 = np.logspace(0, 8, 30)
theta1 = np.logspace(-1, 1, 29)
Theta0, Theta1 = np.meshgrid(theta0, theta1)
LML = [
[
gp_opt.log_marginal_likelihood(np.log([Theta0[i, j], Theta1[i, j]]))
for i in range(Theta0.shape[0])
]
for j in range(Theta0.shape[1])
]
LML = np.array(LML).T
plt.plot(
np.exp(gp_fix.kernel_.theta)[0], np.exp(gp_fix.kernel_.theta)[1], "ko", zorder=10
)
plt.plot(
np.exp(gp_opt.kernel_.theta)[0], np.exp(gp_opt.kernel_.theta)[1], "ko", zorder=10
)
plt.pcolor(Theta0, Theta1, LML)
plt.xscale("log")
plt.yscale("log")
plt.colorbar()
plt.xlabel("Magnitude")
plt.ylabel("Length-scale")
plt.title("Log-marginal-likelihood")
plt.show()
Общее время выполнения скрипта: (0 минут 2.140 секунд)
Связанные примеры
Способность гауссовского процесса регрессии (GPR) оценивать уровень шума данных
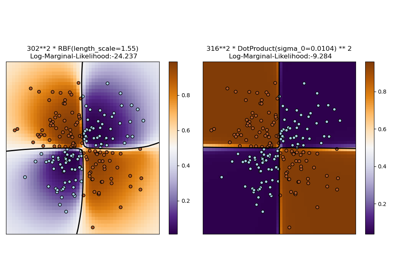
Иллюстрация классификации гауссовским процессом (GPC) на наборе данных XOR
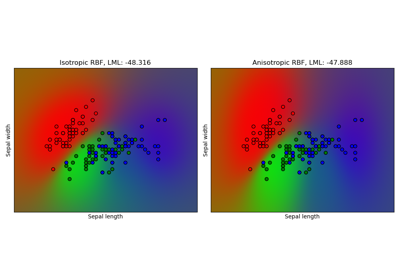
Гауссовский процесс классификации (GPC) на наборе данных iris