Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Регрессия гауссовских процессов: базовый вводный пример#

Простой пример одномерной регрессии, вычисленный двумя разными способами:

Случай без шума
Шумный случай с известным уровнем шума для каждой точки данных

В обоих случаях параметры ядра оцениваются с использованием принципа максимального правдоподобия.

Рисунки иллюстрируют интерполяционное свойство модели Гауссовского процесса, а также его вероятностную природу в виде точечного 95% доверительного интервала.

Обратите внимание, что alpha это параметр для контроля силы регуляризации Тихонова на предполагаемой ковариационной матрице обучающих точек.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Генерация набора данных#

Мы начнём с генерации синтетического набора данных. Истинный процесс генерации определяется как \(f(x) = x \sin(x)\).

import numpy as np

X = np.linspace(start=0, stop=10, num=1_000).reshape(-1, 1)
y = np.squeeze(X * np.sin(X))

import matplotlib.pyplot as plt

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("True generative process")

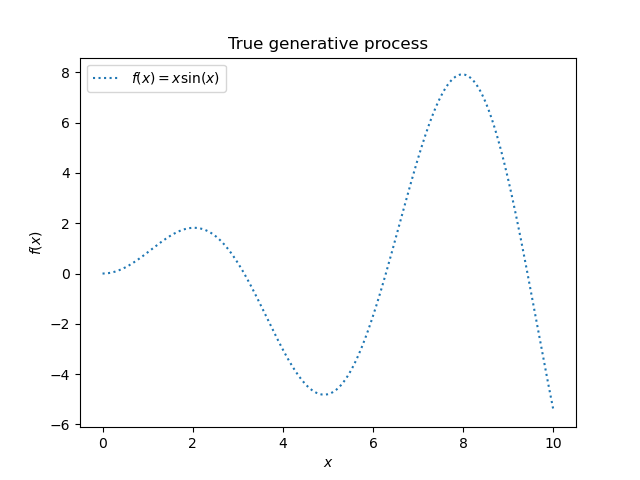
Мы будем использовать этот набор данных в следующем эксперименте, чтобы проиллюстрировать, как работает гауссовская процессная регрессия.

Пример с целевой переменной без шума#

В этом первом примере мы будем использовать истинный генеративный процесс без добавления шума. Для обучения регрессии Гауссовского процесса мы выберем только несколько образцов.

rng = np.random.RandomState(1)
training_indices = rng.choice(np.arange(y.size), size=6, replace=False)
X_train, y_train = X[training_indices], y[training_indices]

Теперь мы подгоняем гауссовский процесс к этим нескольким обучающим образцам данных. Мы будем использовать радиально-базисную функцию (RBF) в качестве ядра и постоянный параметр для подгонки амплитуды.

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

kernel = 1 * RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e2))
gaussian_process = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)
gaussian_process.fit(X_train, y_train)
gaussian_process.kernel_

5.02**2 * RBF(length_scale=1.43)

После обучения нашей модели мы видим, что гиперпараметры ядра были оптимизированы. Теперь мы будем использовать наше ядро для вычисления среднего прогноза по всему набору данных и построим 95% доверительный интервал.

mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.scatter(X_train, y_train, label="Observations")
plt.plot(X, mean_prediction, label="Mean prediction")
plt.fill_between(
    X.ravel(),
    mean_prediction - 1.96 * std_prediction,
    mean_prediction + 1.96 * std_prediction,
    alpha=0.5,
    label=r"95% confidence interval",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("Gaussian process regression on noise-free dataset")

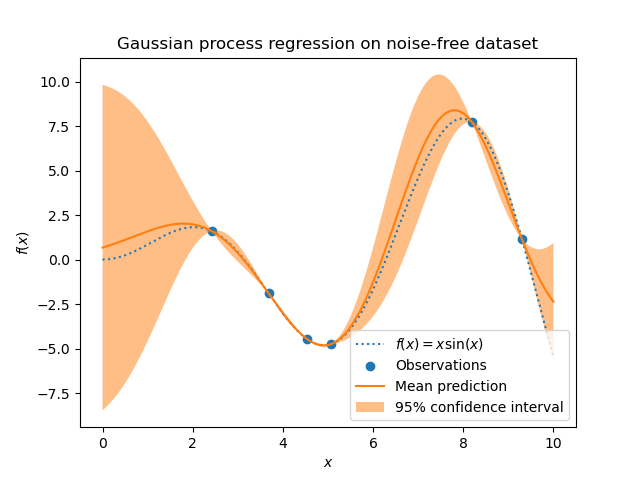
Gaussian process regression on noise-free dataset

Мы видим, что для прогноза, сделанного на точке данных, близкой к обучающей, 95% доверительный интервал имеет малую амплитуду. Когда выборка находится далеко от обучающих данных, прогноз нашей модели менее точен, и предсказание модели менее точно (большая неопределенность).

Пример с зашумленными целевыми значениями#

Мы можем повторить аналогичный эксперимент, добавив дополнительный шум к целевой переменной на этот раз. Это позволит увидеть влияние шума на подобранную модель.

Мы добавляем случайный гауссов шум к цели с произвольным стандартным отклонением.

noise_std = 0.75
y_train_noisy = y_train + rng.normal(loc=0.0, scale=noise_std, size=y_train.shape)

Мы создаем аналогичную модель гауссовского процесса. В дополнение к ядру, на этот раз мы указываем параметр alpha которую можно интерпретировать как дисперсию гауссовского шума.

gaussian_process = GaussianProcessRegressor(
    kernel=kernel, alpha=noise_std**2, n_restarts_optimizer=9
)
gaussian_process.fit(X_train, y_train_noisy)
mean_prediction, std_prediction = gaussian_process.predict(X, return_std=True)

Построим график среднего прогноза и области неопределенности, как и раньше.

plt.plot(X, y, label=r"$f(x) = x \sin(x)$", linestyle="dotted")
plt.errorbar(
    X_train,
    y_train_noisy,
    noise_std,
    linestyle="None",
    color="tab:blue",
    marker=".",
    markersize=10,
    label="Observations",
)
plt.plot(X, mean_prediction, label="Mean prediction")
plt.fill_between(
    X.ravel(),
    mean_prediction - 1.96 * std_prediction,
    mean_prediction + 1.96 * std_prediction,
    color="tab:orange",
    alpha=0.5,
    label=r"95% confidence interval",
)
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
_ = plt.title("Gaussian process regression on a noisy dataset")

Gaussian process regression on a noisy dataset

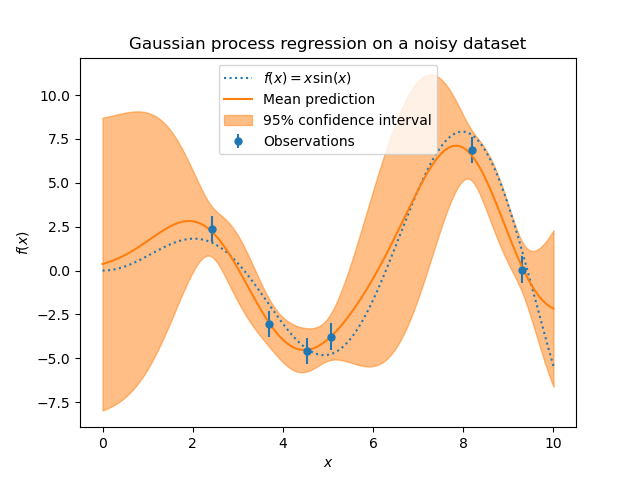
Шум влияет на прогнозы, близкие к обучающим выборкам: прогностическая неопределённость вблизи обучающих выборок больше, потому что мы явно моделируем заданный уровень целевого шума, не зависящий от входной переменной.

Общее время выполнения скрипта: (0 минут 0.440 секунд)