Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Прогнозирование уровня CO2 на наборе данных Mona Loa с использованием гауссовской регрессии (GPR)#
Этот пример основан на разделе 5.4.3 книги «Gaussian Processes for Machine Learning» [1]. Это иллюстрирует пример сложной инженерии ядер и оптимизации гиперпараметров с использованием градиентного подъема по логарифмической маргинальной вероятности. Данные состоят из среднемесячных концентраций атмосферного CO2 (в частях на миллион по объему (ppm)), собранных в обсерватории Мауна-Лоа на Гавайях в период с 1958 по 2001 год. Цель — смоделировать концентрацию CO2 как функцию времени \(t\) и экстраполировать для лет после 2001.
Ссылки
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Построить набор данных#
Мы получим набор данных из обсерватории Мауна-Лоа, которая собирала образцы воздуха. Нас интересует оценка концентрации CO2 и её экстраполяция на последующие годы. Сначала мы загружаем исходный набор данных, доступный в OpenML, как pandas dataframe. Это будет заменено на Polars, как только fetch_openml добавляет встроенную поддержку для этого.
from sklearn.datasets import fetch_openml
co2 = fetch_openml(data_id=41187, as_frame=True)
co2.frame.head()
Сначала мы обрабатываем исходный фрейм данных, чтобы создать столбец даты и выбрать его вместе со столбцом CO2.
import polars as pl
co2_data = pl.DataFrame(co2.frame[["year", "month", "day", "co2"]]).select(
pl.date("year", "month", "day"), "co2"
)
co2_data.head()
co2_data["date"].min(), co2_data["date"].max()
(datetime.date(1958, 3, 29), datetime.date(2001, 12, 29))
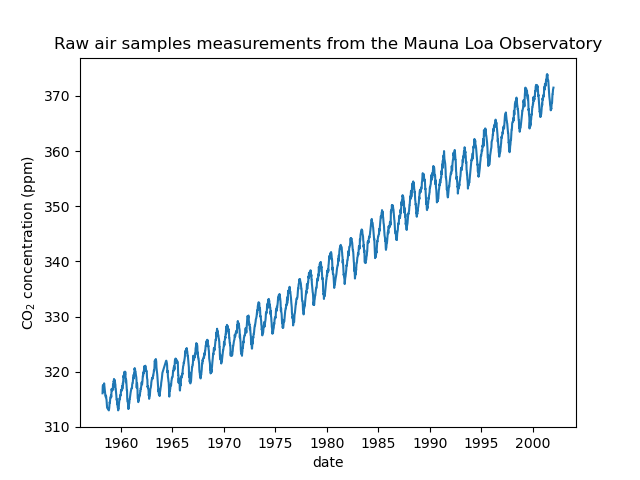
Мы видим, что получаем концентрацию CO2 для некоторых дней с марта 1958 года по декабрь 2001 года. Мы можем построить график исходных данных, чтобы лучше понять ситуацию.
import matplotlib.pyplot as plt
plt.plot(co2_data["date"], co2_data["co2"])
plt.xlabel("date")
plt.ylabel("CO$_2$ concentration (ppm)")
_ = plt.title("Raw air samples measurements from the Mauna Loa Observatory")
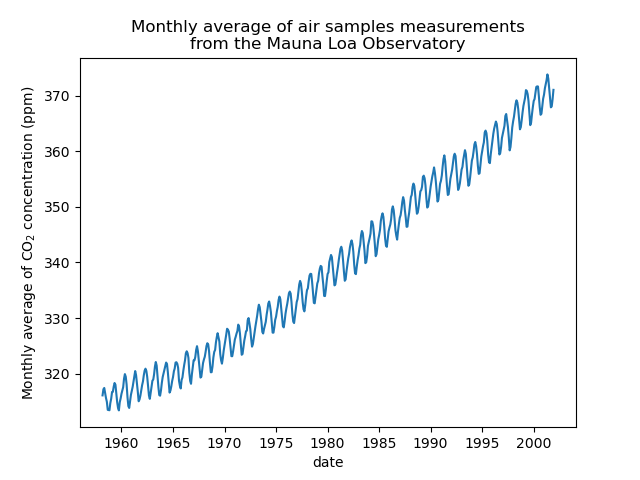
Мы предобработаем набор данных, взяв среднемесячное значение и удалив месяцы, для которых не было собрано измерений. Такая обработка окажет сглаживающий эффект на данные.
co2_data = (
co2_data.sort(by="date")
.group_by_dynamic("date", every="1mo")
.agg(pl.col("co2").mean())
.drop_nulls()
)
plt.plot(co2_data["date"], co2_data["co2"])
plt.xlabel("date")
plt.ylabel("Monthly average of CO$_2$ concentration (ppm)")
_ = plt.title(
"Monthly average of air samples measurements\nfrom the Mauna Loa Observatory"
)
Идея этого примера будет заключаться в прогнозировании концентрации CO2 в зависимости от даты. Мы также заинтересованы в экстраполяции на предстоящие годы после 2001.
В качестве первого шага мы разделим данные и целевую переменную для оценки. Данные, будучи датой, мы преобразуем их в числовые.
X = co2_data.select(
pl.col("date").dt.year() + pl.col("date").dt.month() / 12
).to_numpy()
y = co2_data["co2"].to_numpy()
Спроектировать подходящее ядро#
Чтобы спроектировать ядро для использования с нашим гауссовским процессом, мы можем сделать некоторые предположения относительно имеющихся данных. Мы наблюдаем, что они имеют несколько характеристик: мы видим долгосрочный восходящий тренд, выраженную сезонную вариацию и некоторые меньшие нерегулярности. Мы можем использовать различные подходящие ядра, которые захватят эти особенности.
Во-первых, долгосрочный восходящий тренд может быть аппроксимирован с использованием радиально-базисной функции (RBF) с большим параметром длины масштаба. Ядро RBF с большой длиной масштаба обеспечивает гладкость этого компонента. Возрастающий тренд не навязывается, чтобы предоставить модели степень свободы. Конкретная длина масштаба и амплитуда являются свободными гиперпараметрами.
Сезонные вариации объясняются периодическим экспоненциальным синусоидальным квадратным ядром с фиксированной периодичностью в 1 год. Масштаб длины этой периодической компоненты, контролирующий ее гладкость, является свободным параметром. Чтобы позволить затухание от точной периодичности, берется произведение с ядром RBF. Масштаб длины этого компонента RBF контролирует время затухания и является дополнительным свободным параметром. Этот тип ядра также известен как локально периодическое ядро.
from sklearn.gaussian_process.kernels import ExpSineSquared
seasonal_kernel = (
2.0**2
* RBF(length_scale=100.0)
* ExpSineSquared(length_scale=1.0, periodicity=1.0, periodicity_bounds="fixed")
)
Небольшие нерегулярности объясняются компонентом ядра рационального квадрата, чьи параметры длины и альфа, которые количественно определяют диффузность длин, должны быть определены. Ядро рационального квадрата эквивалентно ядру RBF с несколькими длинами и лучше приспособится к различным нерегулярностям.
from sklearn.gaussian_process.kernels import RationalQuadratic
irregularities_kernel = 0.5**2 * RationalQuadratic(length_scale=1.0, alpha=1.0)
Наконец, шум в наборе данных может быть учтен с помощью ядра, состоящего из вклада ядра RBF, который объясняет коррелированные компоненты шума, такие как локальные погодные явления, и вклада белого ядра для белого шума. Относительные амплитуды и масштаб длины RBF являются дополнительными свободными параметрами.
from sklearn.gaussian_process.kernels import WhiteKernel
noise_kernel = 0.1**2 * RBF(length_scale=0.1) + WhiteKernel(
noise_level=0.1**2, noise_level_bounds=(1e-5, 1e5)
)
Таким образом, наше итоговое ядро является суммой всех предыдущих ядер.
co2_kernel = (
long_term_trend_kernel + seasonal_kernel + irregularities_kernel + noise_kernel
)
co2_kernel
50**2 * RBF(length_scale=50) + 2**2 * RBF(length_scale=100) * ExpSineSquared(length_scale=1, periodicity=1) + 0.5**2 * RationalQuadratic(alpha=1, length_scale=1) + 0.1**2 * RBF(length_scale=0.1) + WhiteKernel(noise_level=0.01)
Обучение модели и экстраполяция#
Теперь мы готовы использовать гауссовский процесс регрессии и обучить его на доступных
данных. Чтобы следовать примеру из литературы, мы вычтем среднее значение
из целевой переменной. Мы могли бы использовать normalize_y=True. Однако, делая это,
мы также масштабировали бы цель (деля y на его стандартное отклонение). Таким образом, гиперпараметры различных ядер имели бы разное значение, поскольку они не были бы выражены в ppm.
from sklearn.gaussian_process import GaussianProcessRegressor
y_mean = y.mean()
gaussian_process = GaussianProcessRegressor(kernel=co2_kernel, normalize_y=False)
gaussian_process.fit(X, y - y_mean)
Теперь мы будем использовать гауссовский процесс для предсказания на:
обучающие данные для проверки качества соответствия;
будущие данные, чтобы увидеть экстраполяцию, выполненную моделью.
Таким образом, мы создаем синтетические данные с 1958 года по текущий месяц. Кроме того, нам нужно добавить вычтенное среднее значение, вычисленное во время обучения.
import datetime
import numpy as np
today = datetime.datetime.now()
current_month = today.year + today.month / 12
X_test = np.linspace(start=1958, stop=current_month, num=1_000).reshape(-1, 1)
mean_y_pred, std_y_pred = gaussian_process.predict(X_test, return_std=True)
mean_y_pred += y_mean
plt.plot(X, y, color="black", linestyle="dashed", label="Measurements")
plt.plot(X_test, mean_y_pred, color="tab:blue", alpha=0.4, label="Gaussian process")
plt.fill_between(
X_test.ravel(),
mean_y_pred - std_y_pred,
mean_y_pred + std_y_pred,
color="tab:blue",
alpha=0.2,
)
plt.legend()
plt.xlabel("Year")
plt.ylabel("Monthly average of CO$_2$ concentration (ppm)")
_ = plt.title(
"Monthly average of air samples measurements\nfrom the Mauna Loa Observatory"
)
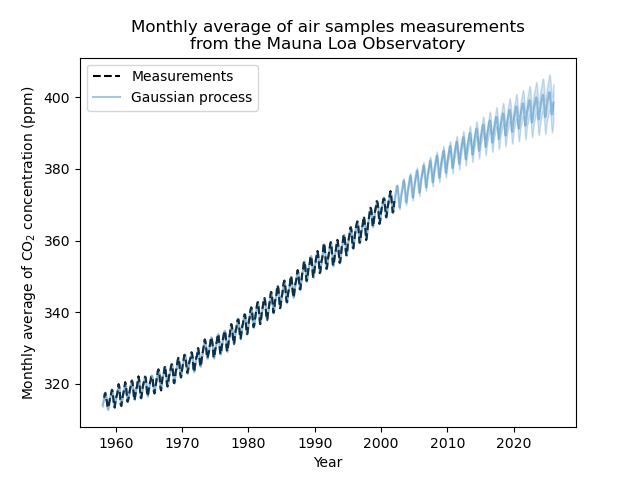
Наша обученная модель способна правильно соответствовать предыдущим данным и экстраполировать на будущие годы с уверенностью.
Интерпретация гиперпараметров ядра#
Теперь мы можем рассмотреть гиперпараметры ядра.
gaussian_process.kernel_
44.8**2 * RBF(length_scale=51.6) + 2.64**2 * RBF(length_scale=91.5) * ExpSineSquared(length_scale=1.48, periodicity=1) + 0.536**2 * RationalQuadratic(alpha=2.89, length_scale=0.968) + 0.188**2 * RBF(length_scale=0.122) + WhiteKernel(noise_level=0.0367)
Таким образом, большая часть сигнала целевой переменной, с вычтенным средним, объясняется долгосрочным возрастающим трендом около ~45 ppm и масштабом длины ~52 года. Периодическая компонента имеет амплитуду ~2.6 ppm, время затухания ~90 лет и масштаб длины ~1.5. Долгое время затухания указывает на то, что у нас есть компонента, очень близкая к сезонной периодичности. Коррелированный шум имеет амплитуду ~0.2 ppm с масштабом длины ~0.12 года и вклад белого шума ~0.04 ppm. Таким образом, общий уровень шума очень мал, что указывает на то, что данные могут быть очень хорошо объяснены моделью.
Общее время выполнения скрипта: (0 минут 4.736 секунд)
Связанные примеры
Регрессия гауссовских процессов: базовый вводный пример
Способность гауссовского процесса регрессии (GPR) оценивать уровень шума данных
Сравнение ядерной гребневой регрессии и регрессии по методу Гауссовских процессов
Гауссовский процесс классификации (GPC) на наборе данных iris