Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
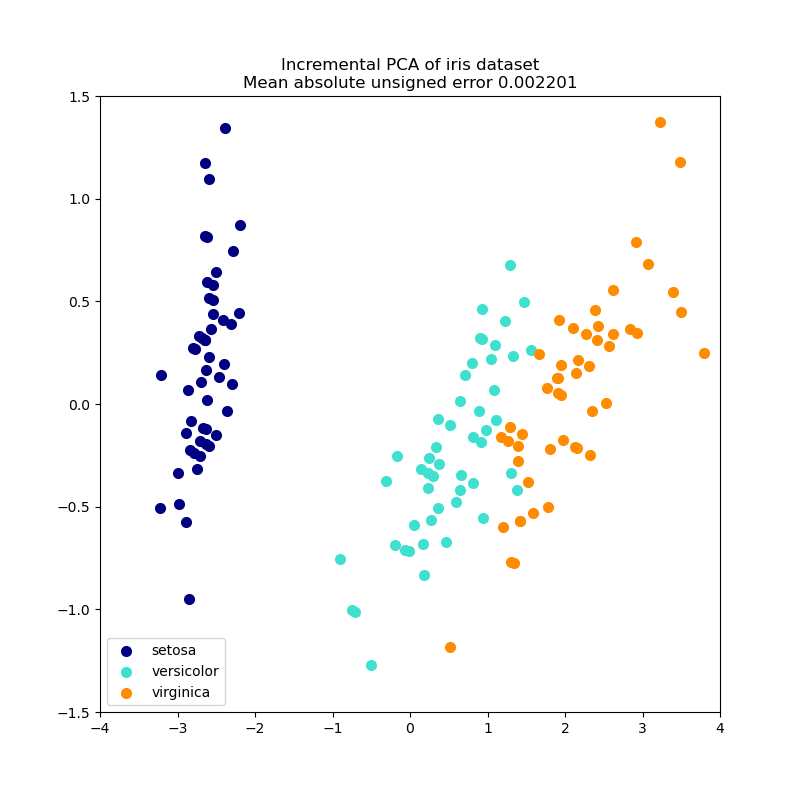
Инкрементальный PCA#
Инкрементальный анализ главных компонент (IPCA) обычно используется как замена анализа главных компонент (PCA), когда набор данных для разложения слишком велик, чтобы поместиться в память. IPCA строит низкоранговое приближение для входных данных, используя объём памяти, не зависящий от количества входных образцов данных. Он всё ещё зависит от признаков входных данных, но изменение размера пакета позволяет контролировать использование памяти.
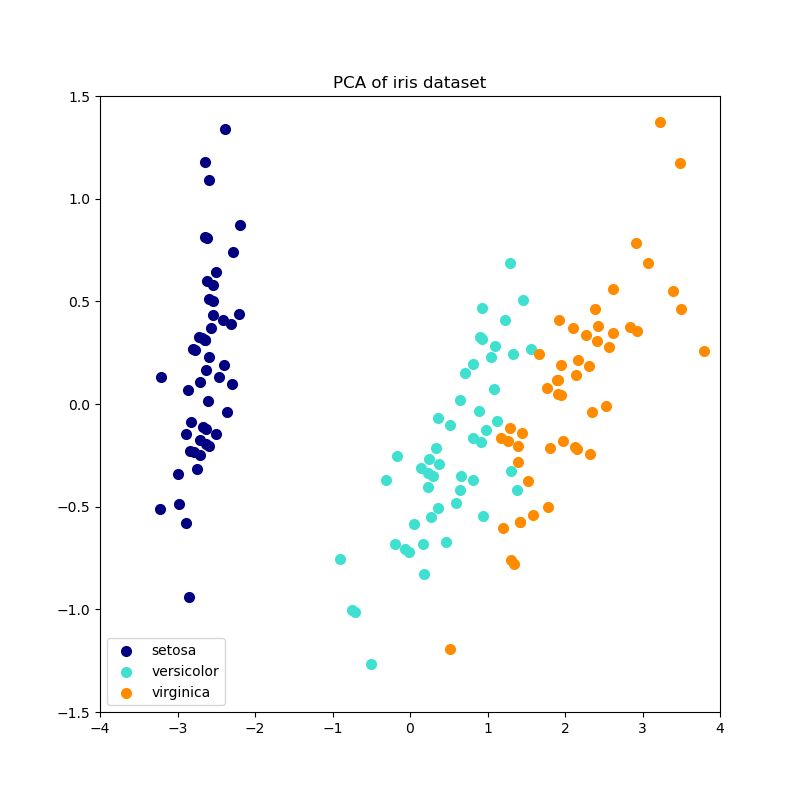
Этот пример служит визуальной проверкой того, что IPCA способен найти схожую проекцию данных с PCA (с точностью до знака), обрабатывая только несколько образцов за раз. Это можно считать "игрушечным примером", так как IPCA предназначен для больших наборов данных, которые не помещаются в оперативную память, требуя инкрементальных подходов.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA, IncrementalPCA
iris = load_iris()
X = iris.data
y = iris.target
n_components = 2
ipca = IncrementalPCA(n_components=n_components, batch_size=10)
X_ipca = ipca.fit_transform(X)
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
colors = ["navy", "turquoise", "darkorange"]
for X_transformed, title in [(X_ipca, "Incremental PCA"), (X_pca, "PCA")]:
plt.figure(figsize=(8, 8))
for color, i, target_name in zip(colors, [0, 1, 2], iris.target_names):
plt.scatter(
X_transformed[y == i, 0],
X_transformed[y == i, 1],
color=color,
lw=2,
label=target_name,
)
if "Incremental" in title:
err = np.abs(np.abs(X_pca) - np.abs(X_ipca)).mean()
plt.title(title + " of iris dataset\nMean absolute unsigned error %.6f" % err)
else:
plt.title(title + " of iris dataset")
plt.legend(loc="best", shadow=False, scatterpoints=1)
plt.axis([-4, 4, -1.5, 1.5])
plt.show()
Общее время выполнения скрипта: (0 минут 0.198 секунд)
Связанные примеры
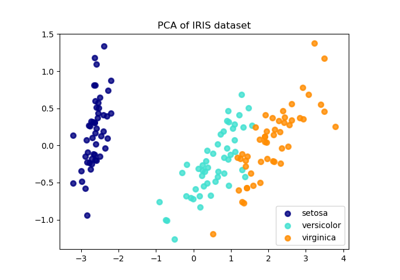
Анализ главных компонент (PCA) на наборе данных Iris
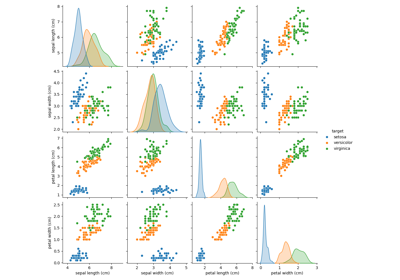
Сравнение LDA и PCA 2D проекции набора данных Iris
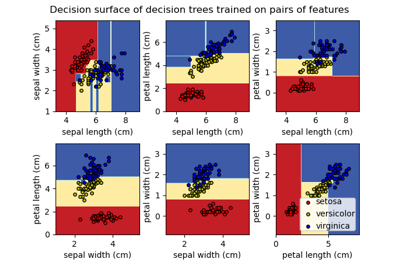
Построить поверхность решений деревьев решений, обученных на наборе данных ирисов
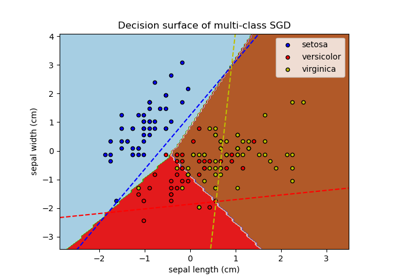
Построение многоклассового SGD на наборе данных iris