Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
FastICA на 2D облаках точек#
Этот пример визуально иллюстрирует в пространстве признаков сравнение результатов с использованием двух различных методов анализа компонент.
Анализ независимых компонент (ICA) против Метод главных компонент (PCA).
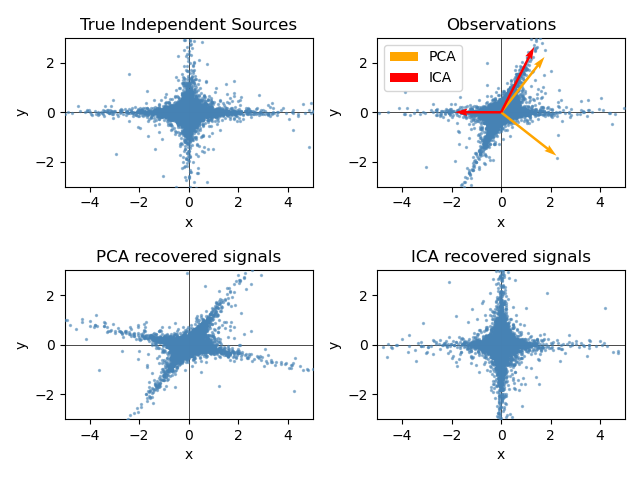
Представление ICA в пространстве признаков дает представление о 'геометрическом ICA': ICA — это алгоритм, который находит направления в пространстве признаков, соответствующие проекциям с высокой негауссовостью. Эти направления не обязательно должны быть ортогональными в исходном пространстве признаков, но они ортогональны в отбеленном пространстве признаков, в котором все направления соответствуют одинаковой дисперсии.
PCA, с другой стороны, находит ортогональные направления в исходном пространстве признаков, которые соответствуют направлениям, объясняющим максимальную дисперсию.
Здесь мы моделируем независимые источники, используя сильно негауссовский процесс, 2 распределения Стьюдента с малым числом степеней свободы (верхний левый рисунок). Мы смешиваем их для создания наблюдений (верхний правый рисунок). В этом исходном пространстве наблюдений направления, идентифицированные PCA, представлены оранжевыми векторами. Мы представляем сигнал в пространстве PCA после отбеливания дисперсией, соответствующей векторам PCA (нижний левый). Запуск ICA соответствует поиску вращения в этом пространстве для идентификации направлений наибольшей негауссовости (нижний правый).
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Сгенерировать тестовые данные#
import numpy as np
from sklearn.decomposition import PCA, FastICA
rng = np.random.RandomState(42)
S = rng.standard_t(1.5, size=(20000, 2))
S[:, 0] *= 2.0
# Mix data
A = np.array([[1, 1], [0, 2]]) # Mixing matrix
X = np.dot(S, A.T) # Generate observations
pca = PCA()
S_pca_ = pca.fit(X).transform(X)
ica = FastICA(random_state=rng, whiten="arbitrary-variance")
S_ica_ = ica.fit(X).transform(X) # Estimate the sources
Построить результаты#
import matplotlib.pyplot as plt
def plot_samples(S, axis_list=None):
plt.scatter(
S[:, 0], S[:, 1], s=2, marker="o", zorder=10, color="steelblue", alpha=0.5
)
if axis_list is not None:
for axis, color, label in axis_list:
x_axis, y_axis = axis / axis.std()
plt.quiver(
(0, 0),
(0, 0),
x_axis,
y_axis,
zorder=11,
width=0.01,
scale=6,
color=color,
label=label,
)
plt.hlines(0, -5, 5, color="black", linewidth=0.5)
plt.vlines(0, -3, 3, color="black", linewidth=0.5)
plt.xlim(-5, 5)
plt.ylim(-3, 3)
plt.gca().set_aspect("equal")
plt.xlabel("x")
plt.ylabel("y")
plt.figure()
plt.subplot(2, 2, 1)
plot_samples(S / S.std())
plt.title("True Independent Sources")
axis_list = [(pca.components_.T, "orange", "PCA"), (ica.mixing_, "red", "ICA")]
plt.subplot(2, 2, 2)
plot_samples(X / np.std(X), axis_list=axis_list)
legend = plt.legend(loc="upper left")
legend.set_zorder(100)
plt.title("Observations")
plt.subplot(2, 2, 3)
plot_samples(S_pca_ / np.std(S_pca_))
plt.title("PCA recovered signals")
plt.subplot(2, 2, 4)
plot_samples(S_ica_ / np.std(S_ica_))
plt.title("ICA recovered signals")
plt.subplots_adjust(0.09, 0.04, 0.94, 0.94, 0.26, 0.36)
plt.tight_layout()
plt.show()
Общее время выполнения скрипта: (0 минут 0.338 секунд)
Связанные примеры
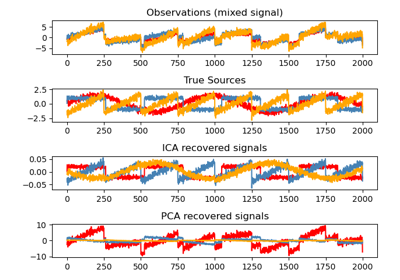
Разделение слепых источников с использованием FastICA
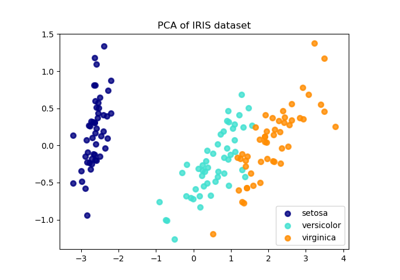
Сравнение LDA и PCA 2D проекции набора данных Iris
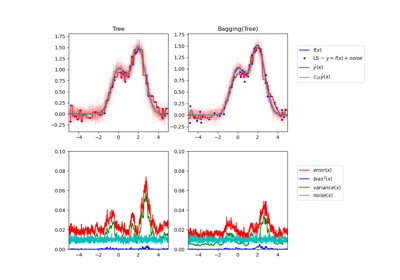
Один оценщик против бэггинга: декомпозиция смещения-дисперсии
Регрессия на главных компонентах против регрессии методом частичных наименьших квадратов