Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Кластеризация текстовых документов с использованием k-means#

Это пример, показывающий, как API scikit-learn можно использовать для кластеризации документов по темам с помощью Bag of Words approach.

Демонстрируются два алгоритма, а именно KMeans и его более масштабируемый вариант, MiniBatchKMeans. Дополнительно, латентный семантический анализ используется для уменьшения размерности и обнаружения скрытых паттернов в данных.

В этом примере используются два разных векторизатора текста: TfidfVectorizer и HashingVectorizer. См. пример блокнота Сравнение FeatureHasher и DictVectorizer для получения дополнительной информации о векторизаторах и сравнении их времени обработки.

Для анализа документов с помощью подхода контролируемого обучения см. пример скрипта Классификация текстовых документов с использованием разреженных признаков.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Загрузка текстовых данных#

Мы загружаем данные из Текстовый набор данных 20 новостных групп, который содержит около 18 000 сообщений новостных групп по 20 темам. Для иллюстративных целей и снижения вычислительных затрат мы выбираем подмножество из 4 тем, содержащих около 3 400 документов. См. пример Классификация текстовых документов с использованием разреженных признаков чтобы получить интуитивное представление о пересечении таких тем.

Обратите внимание, что по умолчанию текстовые выборки содержат некоторую метаинформацию сообщения, такую как "headers", "footers" (сигнатуры) и "quotes" к другим сообщениям. Мы используем remove параметр из fetch_20newsgroups чтобы удалить эти признаки и получить более разумную задачу кластеризации.

import numpy as np

from sklearn.datasets import fetch_20newsgroups

categories = [
    "alt.atheism",
    "talk.religion.misc",
    "comp.graphics",
    "sci.space",
]

dataset = fetch_20newsgroups(
    remove=("headers", "footers", "quotes"),
    subset="all",
    categories=categories,
    shuffle=True,
    random_state=42,
)

labels = dataset.target
unique_labels, category_sizes = np.unique(labels, return_counts=True)
true_k = unique_labels.shape[0]

print(f"{len(dataset.data)} documents - {true_k} categories")

3387 documents - 4 categories

Количественная оценка качества результатов кластеризации#

В этом разделе мы определяем функцию для оценки различных конвейеров кластеризации с использованием нескольких метрик.

Алгоритмы кластеризации по своей сути являются методами обучения без учителя. Однако, поскольку у нас есть метки классов для этого конкретного набора данных, можно использовать метрики оценки, которые используют эту «контролируемую» истинную информацию для количественной оценки качества полученных кластеров. Примеры таких метрик:

гомогенность, которая количественно определяет, насколько кластеры содержат только элементы одного класса;
полнота, которая количественно определяет, насколько члены данного класса назначены одним и тем же кластерам;
V-мера, гармоническое среднее полноты и однородности;
Индекс Рэнда, который измеряет, насколько часто пары точек данных группируются согласованно в соответствии с результатом алгоритма кластеризации и истинным назначением классов;
Скорректированный индекс Рэнда, случайно скорректированный индекс Рэнда, такой что случайное назначение кластеров имеет ожидаемое значение ARI 0.0.

Если истинные метки неизвестны, оценка может быть выполнена только с использованием самих результатов модели. В этом случае пригодится коэффициент силуэта. См. Выбор количества кластеров с помощью анализа силуэта для кластеризации KMeans для примера того, как это сделать.

Для дополнительной информации см. Оценка производительности кластеризации.

from collections import defaultdict
from time import time

from sklearn import metrics

evaluations = []
evaluations_std = []


def fit_and_evaluate(km, X, name=None, n_runs=5):
    name = km.__class__.__name__ if name is None else name

    train_times = []
    scores = defaultdict(list)
    for seed in range(n_runs):
        km.set_params(random_state=seed)
        t0 = time()
        km.fit(X)
        train_times.append(time() - t0)
        scores["Homogeneity"].append(metrics.homogeneity_score(labels, km.labels_))
        scores["Completeness"].append(metrics.completeness_score(labels, km.labels_))
        scores["V-measure"].append(metrics.v_measure_score(labels, km.labels_))
        scores["Adjusted Rand-Index"].append(
            metrics.adjusted_rand_score(labels, km.labels_)
        )
        scores["Silhouette Coefficient"].append(
            metrics.silhouette_score(X, km.labels_, sample_size=2000)
        )
    train_times = np.asarray(train_times)

    print(f"clustering done in {train_times.mean():.2f} ± {train_times.std():.2f} s ")
    evaluation = {
        "estimator": name,
        "train_time": train_times.mean(),
    }
    evaluation_std = {
        "estimator": name,
        "train_time": train_times.std(),
    }
    for score_name, score_values in scores.items():
        mean_score, std_score = np.mean(score_values), np.std(score_values)
        print(f"{score_name}: {mean_score:.3f} ± {std_score:.3f}")
        evaluation[score_name] = mean_score
        evaluation_std[score_name] = std_score
    evaluations.append(evaluation)
    evaluations_std.append(evaluation_std)

Кластеризация K-средних по текстовым признакам#

В этом примере используются два метода извлечения признаков:

TfidfVectorizer использует словарь в памяти (Python dict) для сопоставления наиболее частых слов с индексами признаков и, следовательно, вычисления матрицы частоты встречаемости слов (разреженной). Частоты слов затем перевзвешиваются с использованием вектора обратной частоты документа (IDF), собранного по признакам по всему корпусу.
HashingVectorizer хэширует вхождения слов в фиксированное многомерное пространство, возможно, с коллизиями. Векторы подсчета слов затем нормализуются так, чтобы каждый имел l2-норму, равную единице (спроецирован на евклидову единичную сферу), что, по-видимому, важно для работы k-means в многомерном пространстве.

Кроме того, можно постобработать извлеченные признаки с помощью снижения размерности. Мы исследуем влияние этих выборов на качество кластеризации далее.

Извлечение признаков с использованием TfidfVectorizer#

Сначала мы сравниваем оценщики, используя векторизатор словаря вместе с IDF-нормализацией, предоставляемой TfidfVectorizer.

from sklearn.feature_extraction.text import TfidfVectorizer

vectorizer = TfidfVectorizer(
    max_df=0.5,
    min_df=5,
    stop_words="english",
)
t0 = time()
X_tfidf = vectorizer.fit_transform(dataset.data)

print(f"vectorization done in {time() - t0:.3f} s")
print(f"n_samples: {X_tfidf.shape[0]}, n_features: {X_tfidf.shape[1]}")

vectorization done in 0.405 s
n_samples: 3387, n_features: 7929

После игнорирования терминов, которые встречаются более чем в 50% документов (как установлено max_df=0.5) и термины, которые отсутствуют как минимум в 5 документах (установлено min_df=5), результирующее количество уникальных терминов n_features составляет около 8,000. Мы также можем количественно оценить разреженность X_tfidf матрицы как долю ненулевых элементов, делённую на общее количество элементов.

print(f"{X_tfidf.nnz / np.prod(X_tfidf.shape):.3f}")

0.007

Мы обнаруживаем, что около 0.7% элементов X_tfidf матрицы ненулевые.

Кластеризация разреженных данных с помощью k-средних#

Поскольку оба KMeans и MiniBatchKMeans оптимизировать невыпуклую целевую функцию, их кластеризация не гарантирует оптимальность для данного случайного инициализатора. Более того, на разреженных многомерных данных, таких как текст, векторизованный с использованием подхода Bag of Words, k-средних может инициализировать центроиды на крайне изолированных точках данных. Эти точки данных могут оставаться своими собственными центроидами всё время.

Следующий код иллюстрирует, как предыдущее явление иногда может приводить к сильно несбалансированным кластерам в зависимости от случайной инициализации:

from sklearn.cluster import KMeans

for seed in range(5):
    kmeans = KMeans(
        n_clusters=true_k,
        max_iter=100,
        n_init=1,
        random_state=seed,
    ).fit(X_tfidf)
    cluster_ids, cluster_sizes = np.unique(kmeans.labels_, return_counts=True)
    print(f"Number of elements assigned to each cluster: {cluster_sizes}")
print()
print(
    "True number of documents in each category according to the class labels: "
    f"{category_sizes}"
)

Number of elements assigned to each cluster: [ 481  675 1785  446]
Number of elements assigned to each cluster: [1689  638  480  580]
Number of elements assigned to each cluster: [   1    1    1 3384]
Number of elements assigned to each cluster: [1887  311  332  857]
Number of elements assigned to each cluster: [ 291  673 1771  652]

True number of documents in each category according to the class labels: [799 973 987 628]

Чтобы избежать этой проблемы, одна из возможностей — увеличить количество запусков с независимыми случайными инициализациями n_init. В таком случае выбирается кластеризация с наилучшей инерцией (целевой функцией k-means).

kmeans = KMeans(
    n_clusters=true_k,
    max_iter=100,
    n_init=5,
)

fit_and_evaluate(kmeans, X_tfidf, name="KMeans\non tf-idf vectors")

clustering done in 0.21 ± 0.05 s
Homogeneity: 0.349 ± 0.010
Completeness: 0.398 ± 0.009
V-measure: 0.372 ± 0.009
Adjusted Rand-Index: 0.203 ± 0.017
Silhouette Coefficient: 0.007 ± 0.000

Все эти метрики оценки кластеризации имеют максимальное значение 1.0 (для идеального результата кластеризации). Более высокие значения лучше. Значения скорректированного индекса Рэнда близкие к 0.0 соответствуют случайной маркировке. Обратите внимание из оценок выше, что назначение кластеров действительно значительно выше уровня случайности, но общее качество, безусловно, может быть улучшено.

Имейте в виду, что метки классов могут не точно отражать темы документов, и поэтому метрики, использующие метки, не обязательно являются лучшими для оценки качества нашего конвейера кластеризации.

Выполнение уменьшения размерности с использованием LSA#

A n_init=1 все еще может использоваться, если размерность векторизованного пространства сначала уменьшена, чтобы сделать k-средних более стабильным. Для этой цели мы используем TruncatedSVD, который работает с матрицами количества терминов/tf-idf. Поскольку результаты SVD не нормализованы, мы повторяем нормализацию для улучшения KMeans результат. Использование SVD для уменьшения размерности векторов документов TF-IDF часто называют Латентный семантический анализ (LSA) в литературе по информационному поиску и анализу текстов.

from sklearn.decomposition import TruncatedSVD
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import Normalizer

lsa = make_pipeline(TruncatedSVD(n_components=100), Normalizer(copy=False))
t0 = time()
X_lsa = lsa.fit_transform(X_tfidf)
explained_variance = lsa[0].explained_variance_ratio_.sum()

print(f"LSA done in {time() - t0:.3f} s")
print(f"Explained variance of the SVD step: {explained_variance * 100:.1f}%")

LSA done in 0.436 s
Explained variance of the SVD step: 18.4%

Использование одной инициализации означает, что время обработки будет сокращено для обоих KMeans и MiniBatchKMeans.

kmeans = KMeans(
    n_clusters=true_k,
    max_iter=100,
    n_init=1,
)

fit_and_evaluate(kmeans, X_lsa, name="KMeans\nwith LSA on tf-idf vectors")

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.398 ± 0.011
Completeness: 0.427 ± 0.025
V-measure: 0.412 ± 0.017
Adjusted Rand-Index: 0.321 ± 0.018
Silhouette Coefficient: 0.029 ± 0.001

Мы можем наблюдать, что кластеризация на LSA-представлении документа значительно быстрее (как из-за n_init=1 и потому что размерность пространства признаков LSA намного меньше. Кроме того, все метрики оценки кластеризации улучшились. Мы повторяем эксперимент с MiniBatchKMeans.

from sklearn.cluster import MiniBatchKMeans

minibatch_kmeans = MiniBatchKMeans(
    n_clusters=true_k,
    n_init=1,
    init_size=1000,
    batch_size=1000,
)

fit_and_evaluate(
    minibatch_kmeans,
    X_lsa,
    name="MiniBatchKMeans\nwith LSA on tf-idf vectors",
)

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.333 ± 0.084
Completeness: 0.351 ± 0.066
V-measure: 0.341 ± 0.076
Adjusted Rand-Index: 0.290 ± 0.060
Silhouette Coefficient: 0.026 ± 0.004

Лучшие термины по кластерам#

Поскольку TfidfVectorizer может быть инвертирован, мы можем определить центры кластеров, которые дают интуитивное представление о наиболее влиятельных словах для каждого кластера. См. пример скрипта Классификация текстовых документов с использованием разреженных признаков для сравнения с наиболее предсказательными словами для каждого целевого класса.

original_space_centroids = lsa[0].inverse_transform(kmeans.cluster_centers_)
order_centroids = original_space_centroids.argsort()[:, ::-1]
terms = vectorizer.get_feature_names_out()

for i in range(true_k):
    print(f"Cluster {i}: ", end="")
    for ind in order_centroids[i, :10]:
        print(f"{terms[ind]} ", end="")
    print()

Cluster 0: thanks graphics image know files file program looking software does
Cluster 1: space launch orbit nasa shuttle earth moon like mission just
Cluster 2: god jesus bible believe christian faith people say does christians
Cluster 3: think don people just say know like time did does

HashingVectorizer#

Альтернативная векторизация может быть выполнена с использованием HashingVectorizer экземпляра, который не предоставляет взвешивание IDF, так как это модель без состояния (метод fit ничего не делает). Когда требуется взвешивание IDF, его можно добавить, объединив в конвейер HashingVectorizer вывод в TfidfTransformer экземпляр. В этом случае мы также добавляем LSA в конвейер, чтобы уменьшить размерность и разреженность хэшированного векторного пространства.

from sklearn.feature_extraction.text import HashingVectorizer, TfidfTransformer

lsa_vectorizer = make_pipeline(
    HashingVectorizer(stop_words="english", n_features=50_000),
    TfidfTransformer(),
    TruncatedSVD(n_components=100, random_state=0),
    Normalizer(copy=False),
)

t0 = time()
X_hashed_lsa = lsa_vectorizer.fit_transform(dataset.data)
print(f"vectorization done in {time() - t0:.3f} s")

vectorization done in 2.023 s

Можно заметить, что шаг LSA занимает относительно много времени для обучения, особенно с хешированными векторами. Причина в том, что хешированное пространство обычно большое (установлено в n_features=50_000 в этом примере). Можно попробовать уменьшить количество признаков за счет большей доли признаков с коллизиями хешей, как показано в примере ноутбука Сравнение FeatureHasher и DictVectorizer.

Теперь мы обучаем и оцениваем kmeans и minibatch_kmeans экземпляров на этих хешированных LSA-редуцированных данных:

fit_and_evaluate(kmeans, X_hashed_lsa, name="KMeans\nwith LSA on hashed vectors")

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.390 ± 0.008
Completeness: 0.436 ± 0.012
V-measure: 0.411 ± 0.010
Adjusted Rand-Index: 0.322 ± 0.014
Silhouette Coefficient: 0.030 ± 0.001

fit_and_evaluate(
    minibatch_kmeans,
    X_hashed_lsa,
    name="MiniBatchKMeans\nwith LSA on hashed vectors",
)

clustering done in 0.02 ± 0.00 s
Homogeneity: 0.359 ± 0.053
Completeness: 0.385 ± 0.059
V-measure: 0.371 ± 0.055
Adjusted Rand-Index: 0.315 ± 0.046
Silhouette Coefficient: 0.029 ± 0.002

Оба метода дают хорошие результаты, схожие с запуском тех же моделей на традиционных векторах LSA (без хеширования).

Сводка оценки кластеризации#

import matplotlib.pyplot as plt
import pandas as pd

fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(16, 6), sharey=True)

df = pd.DataFrame(evaluations[::-1]).set_index("estimator")
df_std = pd.DataFrame(evaluations_std[::-1]).set_index("estimator")

df.drop(
    ["train_time"],
    axis="columns",
).plot.barh(ax=ax0, xerr=df_std)
ax0.set_xlabel("Clustering scores")
ax0.set_ylabel("")

df["train_time"].plot.barh(ax=ax1, xerr=df_std["train_time"])
ax1.set_xlabel("Clustering time (s)")
plt.tight_layout()

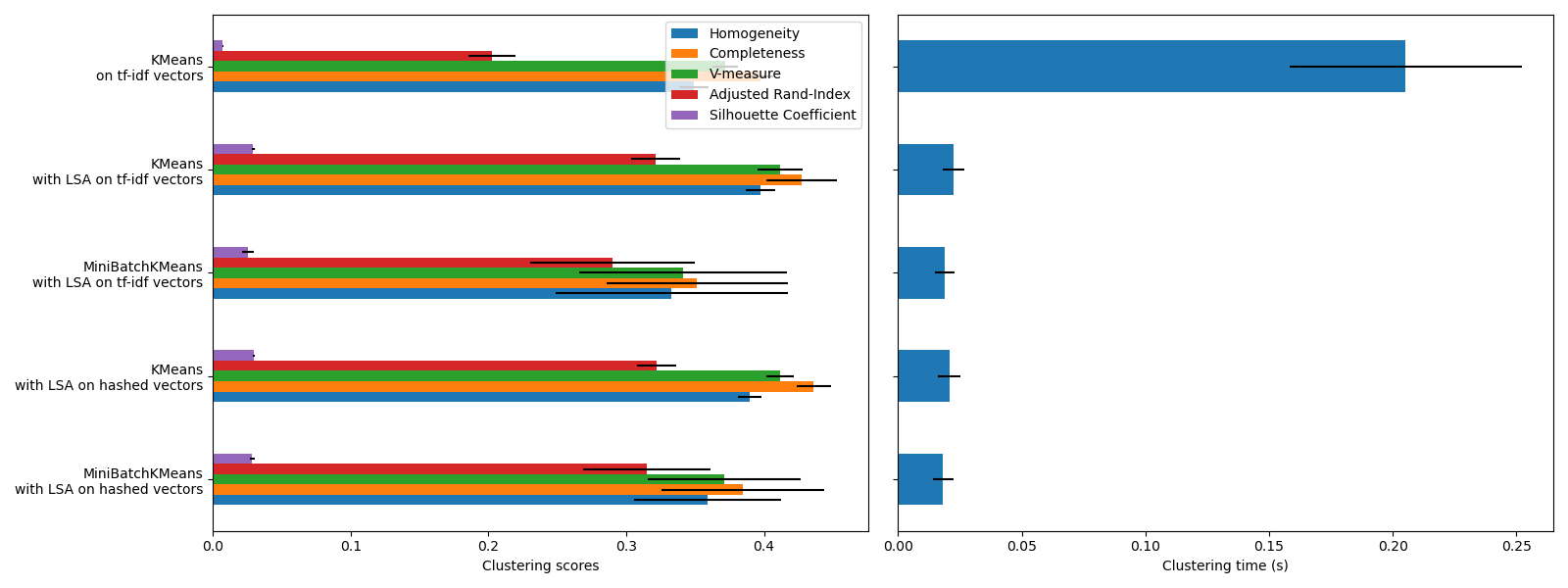
KMeans и MiniBatchKMeans страдают от явления, называемого Проклятие размерности для высокоразмерных наборов данных, таких как текстовые данные. Именно поэтому общие оценки улучшаются при использовании LSA. Использование данных, уменьшенных с помощью LSA, также повышает стабильность и требует меньше времени на кластеризацию, хотя учтите, что сам шаг LSA занимает много времени, особенно с хешированными векторами.

Коэффициент силуэта определяется между 0 и 1. Во всех случаях мы получаем значения близкие к 0 (даже если они немного улучшаются после использования LSA), потому что его определение требует измерения расстояний, в отличие от других метрик оценки, таких как V-мера и скорректированный индекс Рэнда, которые основаны только на назначениях кластеров, а не на расстояниях. Заметьте, что строго говоря, не следует сравнивать коэффициент силуэта между пространствами разной размерности из-за различных понятий расстояния, которые они подразумевают.

Метрики однородности, полноты и, следовательно, v-меры не дают базового уровня для случайной разметки: это означает, что в зависимости от количества образцов, кластеров и истинных классов, полностью случайная разметка не всегда даёт одинаковые значения. В частности, случайная разметка не даст нулевых оценок, особенно когда количество кластеров велико. Эту проблему можно безопасно игнорировать, когда количество образцов больше тысячи, а количество кластеров меньше 10, что имеет место в данном примере. Для меньших размеров выборки или большего количества кластеров безопаснее использовать скорректированный индекс, такой как Adjusted Rand Index (ARI). См. пример Коррекция на случайность в оценке производительности кластеризации для демонстрации эффекта случайной маркировки.

Размер полос ошибок показывает, что MiniBatchKMeans менее стабилен, чем KMeans для этого относительно небольшого набора данных. Более интересно использовать, когда количество образцов значительно больше, но это может привести к небольшому ухудшению качества кластеризации по сравнению с традиционным алгоритмом k-means.

Общее время выполнения скрипта: (0 минут 7.567 секунд)