Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Анализ главных компонент (PCA) на наборе данных Iris#
Этот пример показывает известную технику декомпозиции, называемую методом главных компонент (PCA), на Набор данных Iris.
Этот набор данных состоит из 4 признаков: длина чашелистика, ширина чашелистика, длина лепестка, ширина лепестка. Мы используем PCA для проецирования этого 4-мерного пространства признаков в 3-мерное пространство.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Загрузка набора данных Iris#
Набор данных Iris доступен непосредственно как часть scikit-learn. Его можно загрузить с помощью load_iris функция. С параметрами по умолчанию,
Bunch объект возвращается, содержащий данные,
целевые значения, имена признаков и имена целевых переменных.
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
График пар признаков набора данных Iris#
Давайте сначала построим пары признаков набора данных Iris.
import seaborn as sns
# Rename classes using the iris target names
iris.frame["target"] = iris.target_names[iris.target]
_ = sns.pairplot(iris.frame, hue="target")
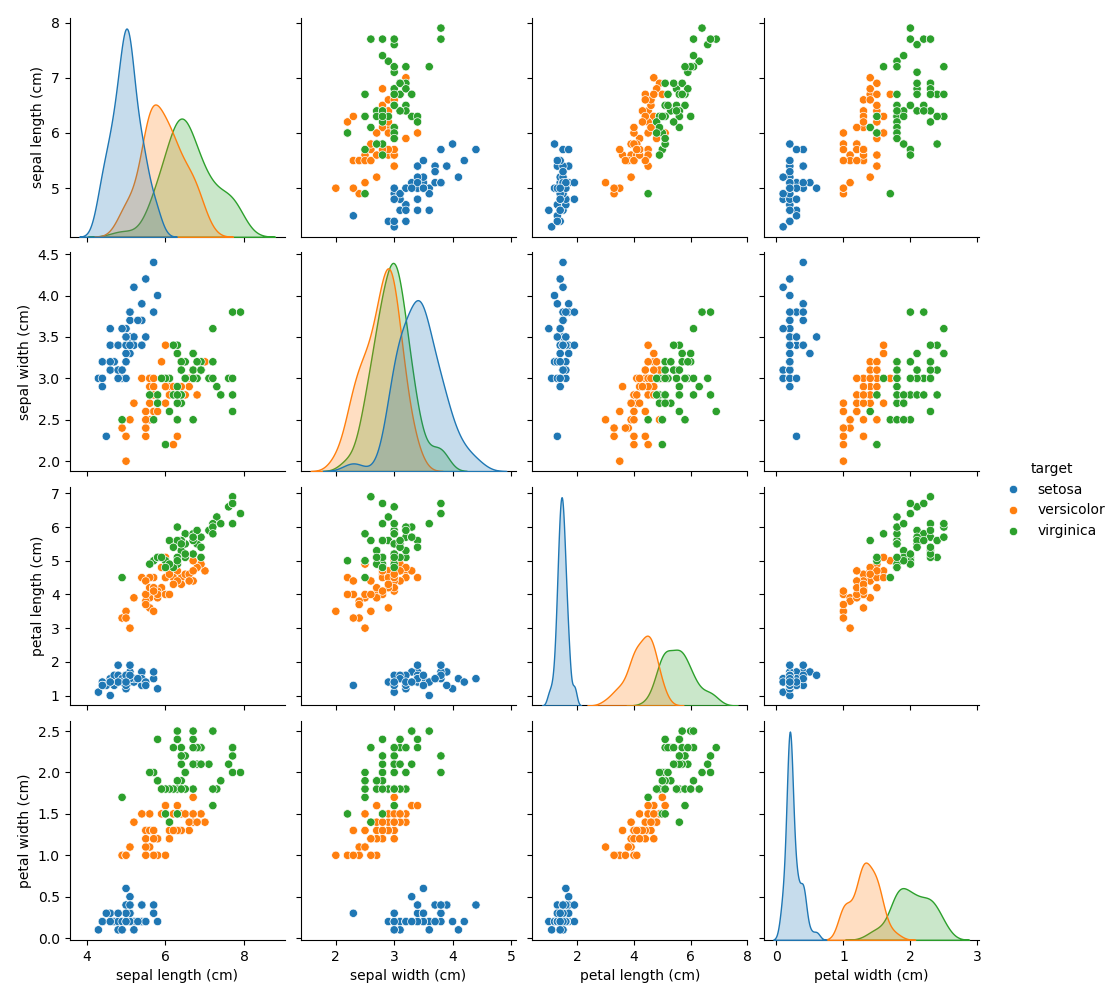
Каждая точка данных на каждой диаграмме рассеяния относится к одному из 150 цветков ириса в наборе данных, с цветом, указывающим их соответствующий тип (Setosa, Versicolor и Virginica).
Вы уже можете увидеть закономерность относительно типа Setosa, который легко идентифицируется на основе его короткой и широкой чашелистика. Только учитывая эти два измерения, ширину и длину чашелистика, все еще есть перекрытие между типами Versicolor и Virginica.
Диагональ графика показывает распределение каждого признака. Мы наблюдаем, что ширина и длина лепестка являются наиболее дискриминантными признаками для трех типов.
Построить представление PCA#
Применим метод главных компонент (PCA) к набору данных ирисов и затем построим график ирисов по первым трём главным компонентам. Это позволит нам лучше дифференцировать три типа!
import matplotlib.pyplot as plt
# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
from sklearn.decomposition import PCA
fig = plt.figure(1, figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d", elev=-150, azim=110)
X_reduced = PCA(n_components=3).fit_transform(iris.data)
scatter = ax.scatter(
X_reduced[:, 0],
X_reduced[:, 1],
X_reduced[:, 2],
c=iris.target,
s=40,
)
ax.set(
title="First three principal components",
xlabel="1st Principal Component",
ylabel="2nd Principal Component",
zlabel="3rd Principal Component",
)
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax.zaxis.set_ticklabels([])
# Add a legend
legend1 = ax.legend(
scatter.legend_elements()[0],
iris.target_names.tolist(),
loc="upper right",
title="Classes",
)
ax.add_artist(legend1)
plt.show()
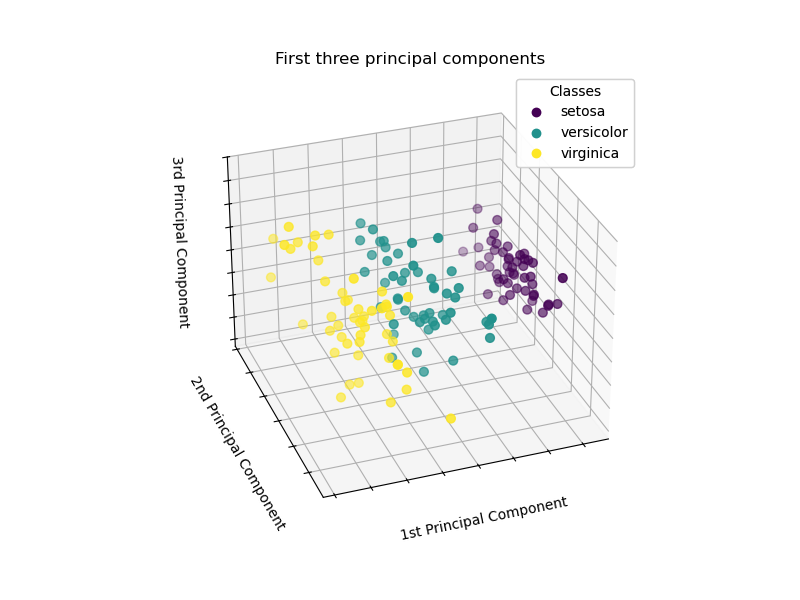
PCA создаст 3 новых признака, которые являются линейной комбинацией 4 исходных признаков. Кроме того, это преобразование максимизирует дисперсию. С этим преобразованием мы можем идентифицировать каждый вид, используя только первую главную компоненту.
Общее время выполнения скрипта: (0 минут 2.060 секунд)
Связанные примеры
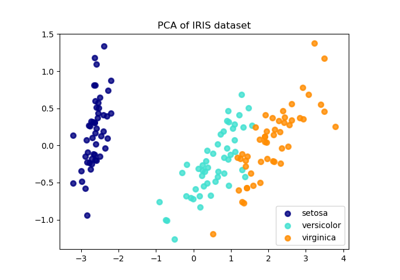
Сравнение LDA и PCA 2D проекции набора данных Iris
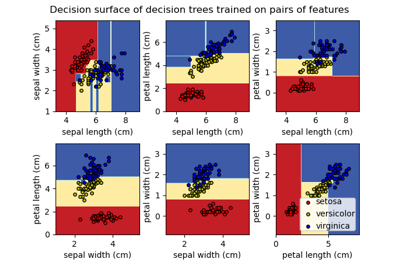
Построить поверхность решений деревьев решений, обученных на наборе данных ирисов
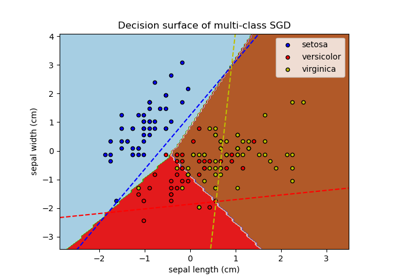
Построение многоклассового SGD на наборе данных iris