Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Ядерный PCA#

Этот пример показывает разницу между методом главных компонент (PCA) и его ядерная версия (KernelPCA).

С одной стороны, мы показываем, что KernelPCA способен найти проекцию данных, которая линейно разделяет их, в то время как это не так с PCA.

Наконец, мы показываем, что инвертирование этой проекции является аппроксимацией с KernelPCA, в то время как он точен с PCA.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Проецирование данных: `PCA` vs. `KernelPCA`#

В этом разделе мы показываем преимущества использования ядра при проецировании данных с помощью метода главных компонент (PCA). Мы создаем набор данных из двух вложенных окружностей.

from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split

X, y = make_circles(n_samples=1_000, factor=0.3, noise=0.05, random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)

Давайте быстро взглянем на сгенерированный набор данных.

import matplotlib.pyplot as plt

_, (train_ax, test_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(8, 4))

train_ax.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
train_ax.set_ylabel("Feature #1")
train_ax.set_xlabel("Feature #0")
train_ax.set_title("Training data")

test_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
test_ax.set_xlabel("Feature #0")
_ = test_ax.set_title("Testing data")

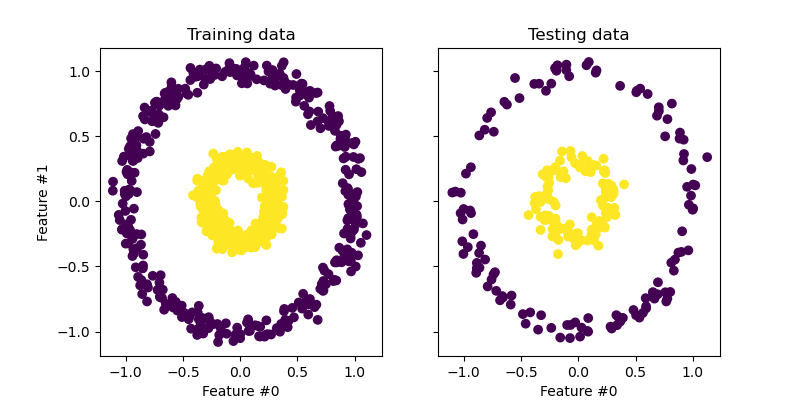
Выборки из каждого класса не могут быть линейно разделены: не существует прямой линии, которая может разделить выборки внутреннего набора от внешнего набора.

Теперь мы используем PCA с ядром и без него, чтобы увидеть эффект использования такого ядра. Используемое ядро — радиально-базисная функция (RBF).

from sklearn.decomposition import PCA, KernelPCA

pca = PCA(n_components=2)
kernel_pca = KernelPCA(
    n_components=None, kernel="rbf", gamma=10, fit_inverse_transform=True, alpha=0.1
)

X_test_pca = pca.fit(X_train).transform(X_test)
X_test_kernel_pca = kernel_pca.fit(X_train).transform(X_test)

fig, (orig_data_ax, pca_proj_ax, kernel_pca_proj_ax) = plt.subplots(
    ncols=3, figsize=(14, 4)
)

orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("Feature #1")
orig_data_ax.set_xlabel("Feature #0")
orig_data_ax.set_title("Testing data")

pca_proj_ax.scatter(X_test_pca[:, 0], X_test_pca[:, 1], c=y_test)
pca_proj_ax.set_ylabel("Principal component #1")
pca_proj_ax.set_xlabel("Principal component #0")
pca_proj_ax.set_title("Projection of testing data\n using PCA")

kernel_pca_proj_ax.scatter(X_test_kernel_pca[:, 0], X_test_kernel_pca[:, 1], c=y_test)
kernel_pca_proj_ax.set_ylabel("Principal component #1")
kernel_pca_proj_ax.set_xlabel("Principal component #0")
_ = kernel_pca_proj_ax.set_title("Projection of testing data\n using KernelPCA")

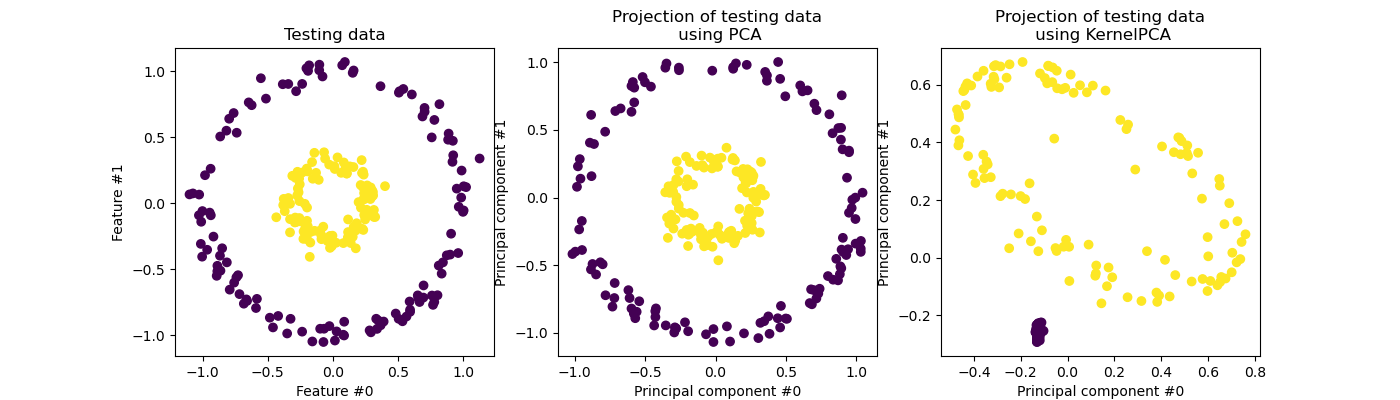
Testing data, Projection of testing data using PCA, Projection of testing data using KernelPCA

Напомним, что PCA линейно преобразует данные. Интуитивно это означает, что система координат будет центрирована, масштабирована по каждой компоненте с учетом её дисперсии и, наконец, повернута. Полученные данные после этого преобразования изотропны и теперь могут быть спроецированы на его главные компоненты.

Таким образом, глядя на проекцию, выполненную с помощью PCA (т.е. на средний рисунок), мы видим, что нет изменений относительно масштабирования; действительно, данные представляют собой два концентрических круга с центром в нуле, исходные данные уже изотропны. Однако мы видим, что данные были повернуты. В заключение, мы видим, что такая проекция не поможет, если определить линейный классификатор для различения выборок обоих классов.

Использование ядра позволяет выполнить нелинейную проекцию. Здесь, используя RBF ядро, мы ожидаем, что проекция развернёт набор данных, сохраняя приблизительно относительные расстояния пар точек данных, которые близки друг к другу в исходном пространстве.

Мы наблюдаем такое поведение на правом рисунке: образцы данного класса ближе друг к другу, чем образцы противоположного класса, разделяя оба набора образцов. Теперь мы можем использовать линейный классификатор для разделения образцов двух классов.

Проецирование в исходное пространство признаков#

Особенность, которую следует учитывать при использовании KernelPCA связано с реконструкцией (т.е. обратной проекцией в исходное пространство признаков). С PCA, реконструкция будет точной, если n_components такое же, как количество исходных признаков. Это так в данном примере.

Мы можем исследовать, получаем ли мы исходный набор данных при обратном проецировании с помощью KernelPCA.

X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstructed_kernel_pca = kernel_pca.inverse_transform(kernel_pca.transform(X_test))

fig, (orig_data_ax, pca_back_proj_ax, kernel_pca_back_proj_ax) = plt.subplots(
    ncols=3, sharex=True, sharey=True, figsize=(13, 4)
)

orig_data_ax.scatter(X_test[:, 0], X_test[:, 1], c=y_test)
orig_data_ax.set_ylabel("Feature #1")
orig_data_ax.set_xlabel("Feature #0")
orig_data_ax.set_title("Original test data")

pca_back_proj_ax.scatter(X_reconstructed_pca[:, 0], X_reconstructed_pca[:, 1], c=y_test)
pca_back_proj_ax.set_xlabel("Feature #0")
pca_back_proj_ax.set_title("Reconstruction via PCA")

kernel_pca_back_proj_ax.scatter(
    X_reconstructed_kernel_pca[:, 0], X_reconstructed_kernel_pca[:, 1], c=y_test
)
kernel_pca_back_proj_ax.set_xlabel("Feature #0")
_ = kernel_pca_back_proj_ax.set_title("Reconstruction via KernelPCA")

Original test data, Reconstruction via PCA, Reconstruction via KernelPCA

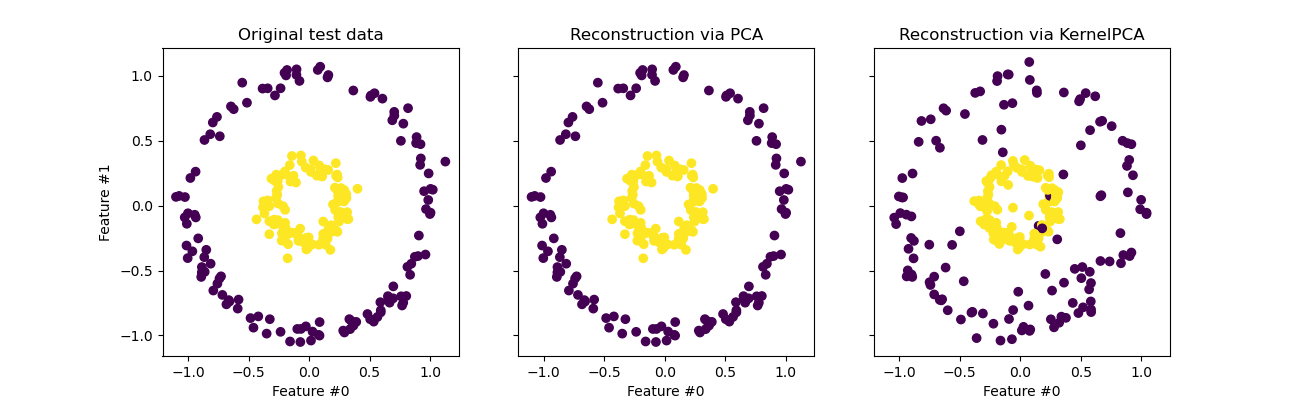
Хотя мы видим идеальную реконструкцию с PCA мы наблюдаем другой результат для KernelPCA.

Действительно, inverse_transform не может полагаться на аналитическую обратную проекцию и, следовательно, на точную реконструкцию. Вместо этого, KernelRidge внутренне обучается для изучения отображения из базиса ядерного PCA в исходное пространство признаков. Этот метод, следовательно, сопровождается аппроксимацией, вносящей небольшие различия при обратном проецировании в исходное пространство признаков.

Чтобы улучшить реконструкцию с использованием inverse_transform, можно настроить alpha в KernelPCA, регуляризационный член, который контролирует зависимость от обучающих данных во время обучения отображения.

Общее время выполнения скрипта: (0 минут 0.539 секунд)