Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Снижение размерности с помощью анализа компонентов соседства#
Пример использования Neighborhood Components Analysis для снижения размерности.
Этот пример сравнивает различные (линейные) методы снижения размерности, примененные к набору данных Digits. Набор данных содержит изображения цифр от 0 до 9 с примерно 180 образцами каждого класса. Каждое изображение имеет размерность 8x8 = 64 и сводится к двумерной точке данных.
Метод главных компонент (PCA), применённый к этим данным, определяет комбинацию атрибутов (главные компоненты или направления в пространстве признаков), которые объясняют наибольшую дисперсию в данных. Здесь мы отображаем различные образцы на первых двух главных компонентах.
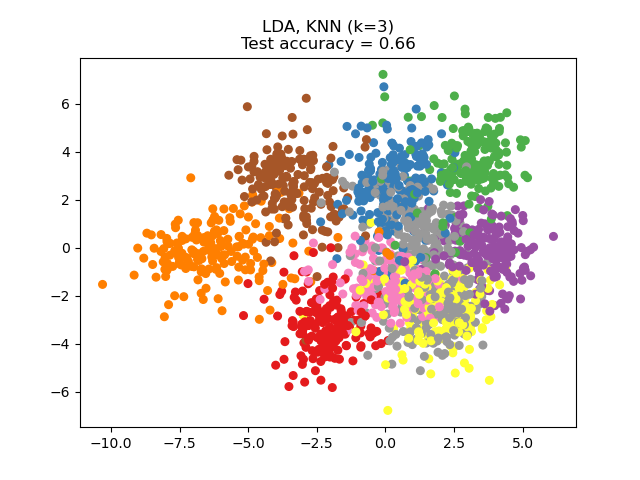
Линейный дискриминантный анализ (LDA) пытается идентифицировать атрибуты, которые объясняют наибольшую дисперсию между классами. В частности, LDA, в отличие от PCA, является контролируемым методом, использующим известные метки классов.
Анализ компонентов соседства (NCA) пытается найти пространство признаков, в котором стохастический алгоритм ближайших соседей даст наилучшую точность. Как и LDA, это контролируемый метод.
Можно заметить, что NCA обеспечивает кластеризацию данных, которая визуально значима, несмотря на большое снижение размерности.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier, NeighborhoodComponentsAnalysis
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
n_neighbors = 3
random_state = 0
# Load Digits dataset
X, y = datasets.load_digits(return_X_y=True)
# Split into train/test
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.5, stratify=y, random_state=random_state
)
dim = len(X[0])
n_classes = len(np.unique(y))
# Reduce dimension to 2 with PCA
pca = make_pipeline(StandardScaler(), PCA(n_components=2, random_state=random_state))
# Reduce dimension to 2 with LinearDiscriminantAnalysis
lda = make_pipeline(StandardScaler(), LinearDiscriminantAnalysis(n_components=2))
# Reduce dimension to 2 with NeighborhoodComponentAnalysis
nca = make_pipeline(
StandardScaler(),
NeighborhoodComponentsAnalysis(n_components=2, random_state=random_state),
)
# Use a nearest neighbor classifier to evaluate the methods
knn = KNeighborsClassifier(n_neighbors=n_neighbors)
# Make a list of the methods to be compared
dim_reduction_methods = [("PCA", pca), ("LDA", lda), ("NCA", nca)]
# plt.figure()
for i, (name, model) in enumerate(dim_reduction_methods):
plt.figure()
# plt.subplot(1, 3, i + 1, aspect=1)
# Fit the method's model
model.fit(X_train, y_train)
# Fit a nearest neighbor classifier on the embedded training set
knn.fit(model.transform(X_train), y_train)
# Compute the nearest neighbor accuracy on the embedded test set
acc_knn = knn.score(model.transform(X_test), y_test)
# Embed the data set in 2 dimensions using the fitted model
X_embedded = model.transform(X)
# Plot the projected points and show the evaluation score
plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, s=30, cmap="Set1")
plt.title(
"{}, KNN (k={})\nTest accuracy = {:.2f}".format(name, n_neighbors, acc_knn)
)
plt.show()
Общее время выполнения скрипта: (0 минут 1.730 секунд)
Связанные примеры
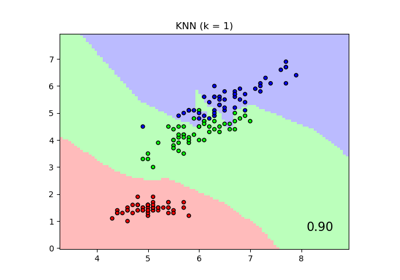
Сравнение ближайших соседей с анализом компонент соседства и без него
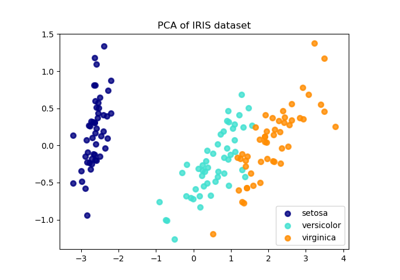
Сравнение LDA и PCA 2D проекции набора данных Iris
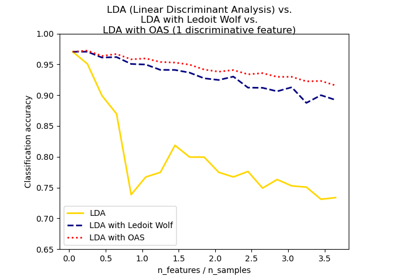
Нормальный, Ledoit-Wolf и OAS линейный дискриминантный анализ для классификации