Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Иллюстрация анализа компонентов соседства#
Этот пример иллюстрирует изученную метрику расстояния, которая максимизирует точность классификации ближайших соседей. Он предоставляет визуальное представление этой метрики по сравнению с исходным пространством точек. Пожалуйста, обратитесь к Руководство пользователя для получения дополнительной информации.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from scipy.special import logsumexp
from sklearn.datasets import make_classification
from sklearn.neighbors import NeighborhoodComponentsAnalysis
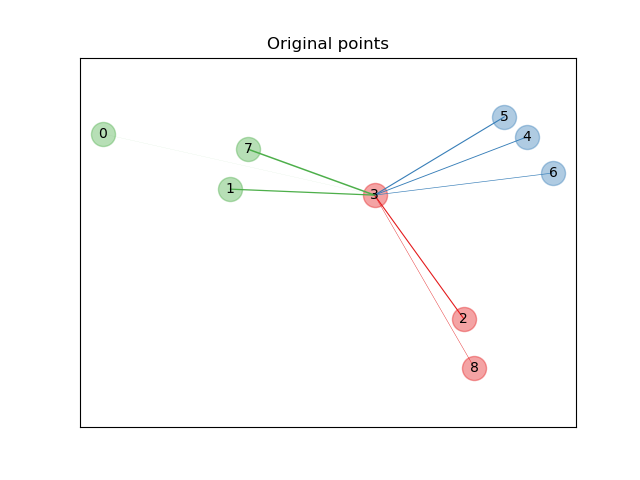
Исходные точки#
Сначала мы создаем набор данных из 9 образцов из 3 классов и отображаем точки в исходном пространстве. Для этого примера мы сосредоточимся на классификации точки №3. Толщина связи между точкой №3 и другой точкой пропорциональна их расстоянию.
X, y = make_classification(
n_samples=9,
n_features=2,
n_informative=2,
n_redundant=0,
n_classes=3,
n_clusters_per_class=1,
class_sep=1.0,
random_state=0,
)
plt.figure(1)
ax = plt.gca()
for i in range(X.shape[0]):
ax.text(X[i, 0], X[i, 1], str(i), va="center", ha="center")
ax.scatter(X[i, 0], X[i, 1], s=300, c=cm.Set1(y[[i]]), alpha=0.4)
ax.set_title("Original points")
ax.axes.get_xaxis().set_visible(False)
ax.axes.get_yaxis().set_visible(False)
ax.axis("equal") # so that boundaries are displayed correctly as circles
def link_thickness_i(X, i):
diff_embedded = X[i] - X
dist_embedded = np.einsum("ij,ij->i", diff_embedded, diff_embedded)
dist_embedded[i] = np.inf
# compute exponentiated distances (use the log-sum-exp trick to
# avoid numerical instabilities
exp_dist_embedded = np.exp(-dist_embedded - logsumexp(-dist_embedded))
return exp_dist_embedded
def relate_point(X, i, ax):
pt_i = X[i]
for j, pt_j in enumerate(X):
thickness = link_thickness_i(X, i)
if i != j:
line = ([pt_i[0], pt_j[0]], [pt_i[1], pt_j[1]])
ax.plot(*line, c=cm.Set1(y[j]), linewidth=5 * thickness[j])
i = 3
relate_point(X, i, ax)
plt.show()
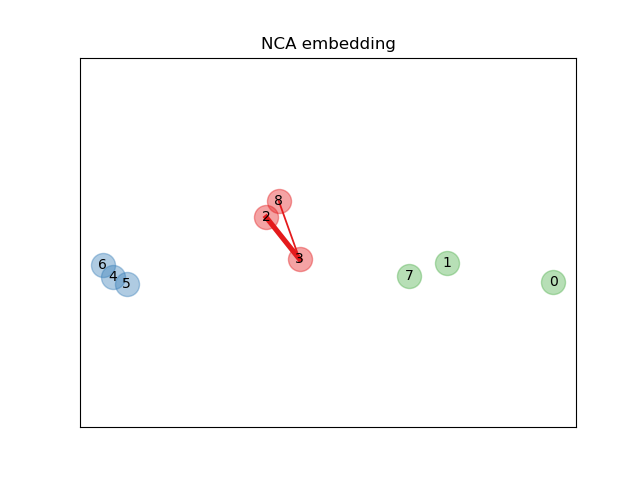
Обучение эмбеддингу#
Мы используем NeighborhoodComponentsAnalysis для обучения
вложения и построения точек после преобразования. Затем мы берем
вложение и находим ближайших соседей.
nca = NeighborhoodComponentsAnalysis(max_iter=30, random_state=0)
nca = nca.fit(X, y)
plt.figure(2)
ax2 = plt.gca()
X_embedded = nca.transform(X)
relate_point(X_embedded, i, ax2)
for i in range(len(X)):
ax2.text(X_embedded[i, 0], X_embedded[i, 1], str(i), va="center", ha="center")
ax2.scatter(X_embedded[i, 0], X_embedded[i, 1], s=300, c=cm.Set1(y[[i]]), alpha=0.4)
ax2.set_title("NCA embedding")
ax2.axes.get_xaxis().set_visible(False)
ax2.axes.get_yaxis().set_visible(False)
ax2.axis("equal")
plt.show()
Общее время выполнения скрипта: (0 минут 0.124 секунд)
Связанные примеры
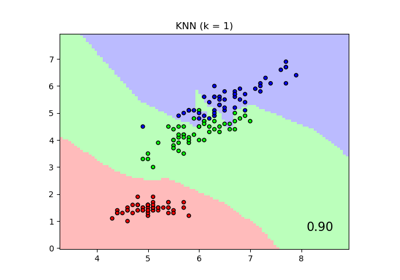
Сравнение ближайших соседей с анализом компонент соседства и без него
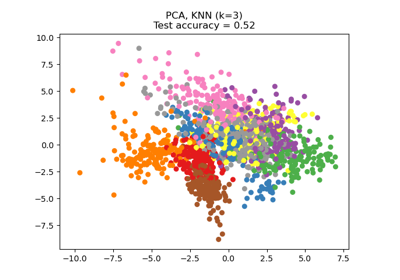
Снижение размерности с помощью анализа компонентов соседства

Обучение многообразию на рукописных цифрах: Locally Linear Embedding, Isomap…
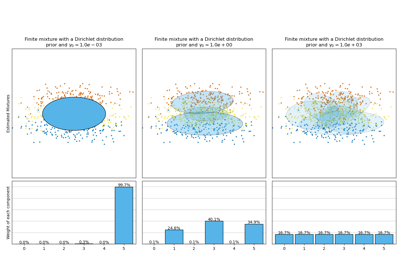
Анализ вариации байесовской гауссовой смеси с априорным типом концентрации