Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Признаки в деревьях с градиентным бустингом на гистограммах#

Градиентный бустинг на основе гистограмм (HGBT) модели могут быть одними из самых полезных моделей обучения с учителем в scikit-learn. Они основаны на современной реализации градиентного бустинга, сравнимой с LightGBM и XGBoost. Таким образом, модели HGBT более функционально богаты и часто превосходят альтернативные модели, такие как случайные леса, особенно когда количество образцов больше нескольких десятков тысяч (см. Сравнение моделей случайных лесов и градиентного бустинга на гистограммах).

Основные удобные функции моделей HGBT:

Несколько доступных функций потерь для задач регрессии среднего значения и квантилей, см. Квантильная потеря.
Поддержка категориальных признаков, см. Поддержка категориальных признаков в градиентном бустинге.
Ранняя остановка.
Поддержка пропущенных значений, что позволяет избежать необходимости в импутере.
Монотонные ограничения.
Ограничения взаимодействий.

Этот пример демонстрирует все пункты, кроме 2 и 6, в реальных условиях.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Подготовка данных#

The набор данных electricity состоит из данных, собранных с рынка электроэнергии Нового Южного Уэльса в Австралии. На этом рынке цены не фиксированы и зависят от спроса и предложения. Они устанавливаются каждые пять минут. Передачи электроэнергии в/из соседнего штата Виктория осуществлялись для смягчения колебаний.

Набор данных, первоначально названный ELEC2, содержит 45 312 экземпляров, датированных с 7 мая 1996 года по 5 декабря 1998 года. Каждый образец набора данных относится к периоду в 30 минут, т.е. существует 48 экземпляров для каждого временного периода одного дня. Каждый образец в наборе данных имеет 7 столбцов:

дата: с 7 мая 1996 по 5 декабря 1998. Нормализовано между 0 и 1;
день: день недели (1-7);
период: получасовые интервалы в течение 24 часов. Нормализовано между 0 и 1;
nswprice/nswdemand: цена/спрос на электроэнергию в Новом Южном Уэльсе;
vicprice/vicdemand: цена/спрос на электроэнергию в Виктории.

Изначально это задача классификации, но здесь мы используем ее для задачи регрессии, чтобы предсказать запланированную передачу электроэнергии между штатами.

from sklearn.datasets import fetch_openml

electricity = fetch_openml(
    name="electricity", version=1, as_frame=True, parser="pandas"
)
df = electricity.frame

Этот конкретный набор данных имеет ступенчато постоянную цель для первых 17 760 образцов:

df["transfer"][:17_760].unique()

array([0.414912, 0.500526])

Давайте удалим эти записи и исследуем почасовую передачу электроэнергии в разные дни недели:

import matplotlib.pyplot as plt
import seaborn as sns

df = electricity.frame.iloc[17_760:]
X = df.drop(columns=["transfer", "class"])
y = df["transfer"]

fig, ax = plt.subplots(figsize=(15, 10))
pointplot = sns.lineplot(x=df["period"], y=df["transfer"], hue=df["day"], ax=ax)
handles, labels = ax.get_legend_handles_labels()
ax.set(
    title="Hourly energy transfer for different days of the week",
    xlabel="Normalized time of the day",
    ylabel="Normalized energy transfer",
)
_ = ax.legend(handles, ["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"])

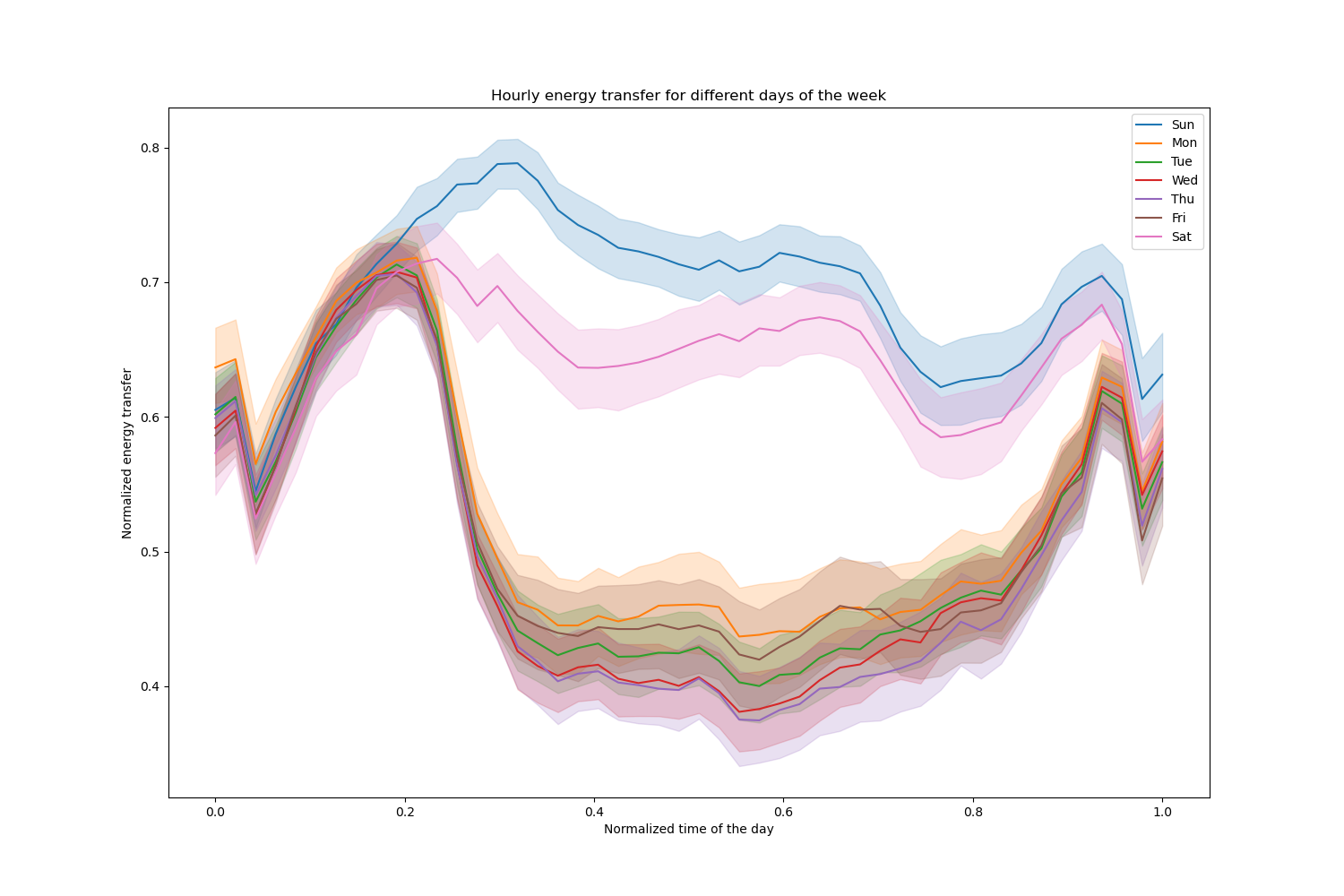
Hourly energy transfer for different days of the week

Заметьте, что передача энергии систематически увеличивается в выходные дни.

Влияние количества деревьев и ранней остановки#

Для иллюстрации эффекта (максимального) количества деревьев мы обучаем HistGradientBoostingRegressor по ежедневной передаче электроэнергии с использованием всего набора данных. Затем мы визуализируем его предсказания в зависимости от max_iter параметр. Здесь мы не пытаемся оценить производительность модели и её способность к обобщению, а скорее её способность обучаться на тренировочных данных.

from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, shuffle=False)

print(f"Training sample size: {X_train.shape[0]}")
print(f"Test sample size: {X_test.shape[0]}")
print(f"Number of features: {X_train.shape[1]}")

Training sample size: 16531
Test sample size: 11021
Number of features: 7

max_iter_list = [5, 50]
average_week_demand = (
    df.loc[X_test.index].groupby(["day", "period"], observed=False)["transfer"].mean()
)
colors = sns.color_palette("colorblind")
fig, ax = plt.subplots(figsize=(10, 5))
average_week_demand.plot(color=colors[0], label="recorded average", linewidth=2, ax=ax)

for idx, max_iter in enumerate(max_iter_list):
    hgbt = HistGradientBoostingRegressor(
        max_iter=max_iter, categorical_features=None, random_state=42
    )
    hgbt.fit(X_train, y_train)

    y_pred = hgbt.predict(X_test)
    prediction_df = df.loc[X_test.index].copy()
    prediction_df["y_pred"] = y_pred
    average_pred = prediction_df.groupby(["day", "period"], observed=False)[
        "y_pred"
    ].mean()
    average_pred.plot(
        color=colors[idx + 1], label=f"max_iter={max_iter}", linewidth=2, ax=ax
    )

ax.set(
    title="Predicted average energy transfer during the week",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["Sun", "Mon", "Tue", "Wed", "Thu", "Fri", "Sat"],
    xlabel="Time of the week",
    ylabel="Normalized energy transfer",
)
_ = ax.legend()

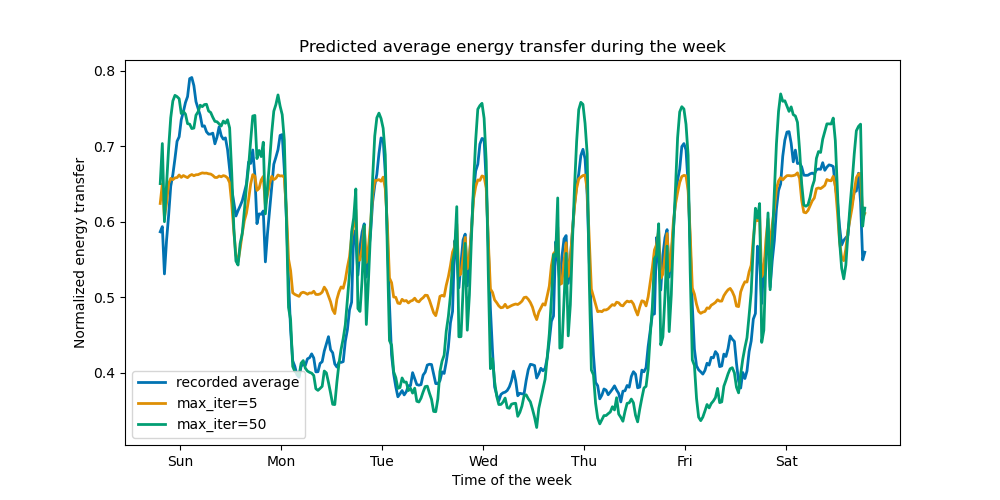
Predicted average energy transfer during the week

Всего за несколько итераций модели HGBT могут достичь сходимости (см. Сравнение моделей случайных лесов и градиентного бустинга на гистограммах), что означает, что добавление большего количества деревьев больше не улучшает модель. На рисунке выше 5 итераций недостаточно для получения хороших предсказаний. С 50 итерациями мы уже можем хорошо справиться.

Установка max_iter слишком высокое значение может ухудшить качество прогнозирования и потребовать много вычислительных ресурсов, которых можно избежать. Поэтому реализация HGBT в scikit-learn предоставляет автоматический ранняя остановка стратегия. С ней модель использует часть обучающих данных в качестве внутреннего проверочного набора (validation_fraction) и останавливает обучение, если оценка валидации не улучшается (или ухудшается) после n_iter_no_change итерации до определенного допуска (tol).

Обратите внимание, что существует компромисс между learning_rate и max_iter: Обычно меньшие скорости обучения предпочтительнее, но требуют больше итераций для сходимости к минимальной потере, в то время как большие скорости обучения сходятся быстрее (меньше итераций/деревьев требуется), но за счет большей минимальной потери.

Из-за высокой корреляции между скоростью обучения и количеством итераций, хорошей практикой является настройка скорости обучения вместе со всеми (важными) другими гиперпараметрами, обучение HBGT на тренировочном наборе с достаточно большим значением для max_iter и определить наилучший max_iter через раннюю остановку и некоторые явные validation_fraction.

common_params = {
    "max_iter": 1_000,
    "learning_rate": 0.3,
    "validation_fraction": 0.2,
    "random_state": 42,
    "categorical_features": None,
    "scoring": "neg_root_mean_squared_error",
}

hgbt = HistGradientBoostingRegressor(early_stopping=True, **common_params)
hgbt.fit(X_train, y_train)

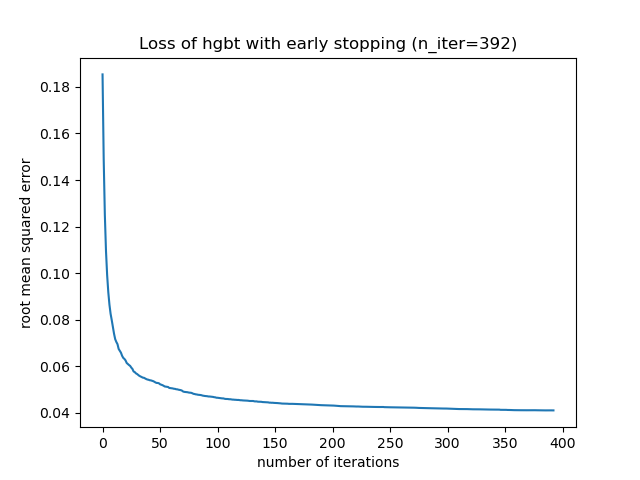
_, ax = plt.subplots()
plt.plot(-hgbt.validation_score_)
_ = ax.set(
    xlabel="number of iterations",
    ylabel="root mean squared error",
    title=f"Loss of hgbt with early stopping (n_iter={hgbt.n_iter_})",
)

Loss of hgbt with early stopping (n_iter=392)

Затем мы можем перезаписать значение для max_iter до разумного значения и избежать дополнительных вычислительных затрат на внутреннюю валидацию. Округление количества итераций может учесть изменчивость обучающего набора:

import math

common_params["max_iter"] = math.ceil(hgbt.n_iter_ / 100) * 100
common_params["early_stopping"] = False
hgbt = HistGradientBoostingRegressor(**common_params)

Примечание

Внутренняя валидация, выполняемая во время ранней остановки, не оптимальна для временных рядов.

Поддержка пропущенных значений#

Модели HGBT имеют встроенную поддержку пропущенных значений. Во время обучения дерево решает, куда должны идти образцы с пропущенными значениями (левый или правый дочерний узел) на каждом разбиении, на основе потенциального выигрыша. При прогнозировании эти образцы отправляются в соответствующий изученный дочерний узел. Если у признака не было пропущенных значений во время обучения, то для прогнозирования образцы с пропущенными значениями для этого признака отправляются в дочерний узел с наибольшим количеством образцов (как было замечено во время обучения).

Данный пример показывает, как регрессии HGBT обрабатывают значения, пропущенные полностью случайным образом (MCAR), т.е. когда пропуск не зависит от наблюдаемых или ненаблюдаемых данных. Мы можем смоделировать такой сценарий, случайно заменяя значения из случайно выбранных признаков на nan значения.

import numpy as np

from sklearn.metrics import root_mean_squared_error

rng = np.random.RandomState(42)
first_week = slice(0, 336)  # first week in the test set as 7 * 48 = 336
missing_fraction_list = [0, 0.01, 0.03]


def generate_missing_values(X, missing_fraction):
    total_cells = X.shape[0] * X.shape[1]
    num_missing_cells = int(total_cells * missing_fraction)
    row_indices = rng.choice(X.shape[0], num_missing_cells, replace=True)
    col_indices = rng.choice(X.shape[1], num_missing_cells, replace=True)
    X_missing = X.copy()
    X_missing.iloc[row_indices, col_indices] = np.nan
    return X_missing


fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="Actual transfer")

for missing_fraction in missing_fraction_list:
    X_train_missing = generate_missing_values(X_train, missing_fraction)
    X_test_missing = generate_missing_values(X_test, missing_fraction)
    hgbt.fit(X_train_missing, y_train)
    y_pred = hgbt.predict(X_test_missing[first_week])
    rmse = root_mean_squared_error(y_test[first_week], y_pred)
    ax.plot(
        y_pred[first_week],
        label=f"missing_fraction={missing_fraction}, RMSE={rmse:.3f}",
        alpha=0.5,
    )
ax.set(
    title="Daily energy transfer predictions on data with MCAR values",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
    xlabel="Time of the week",
    ylabel="Normalized energy transfer",
)
_ = ax.legend(loc="lower right")

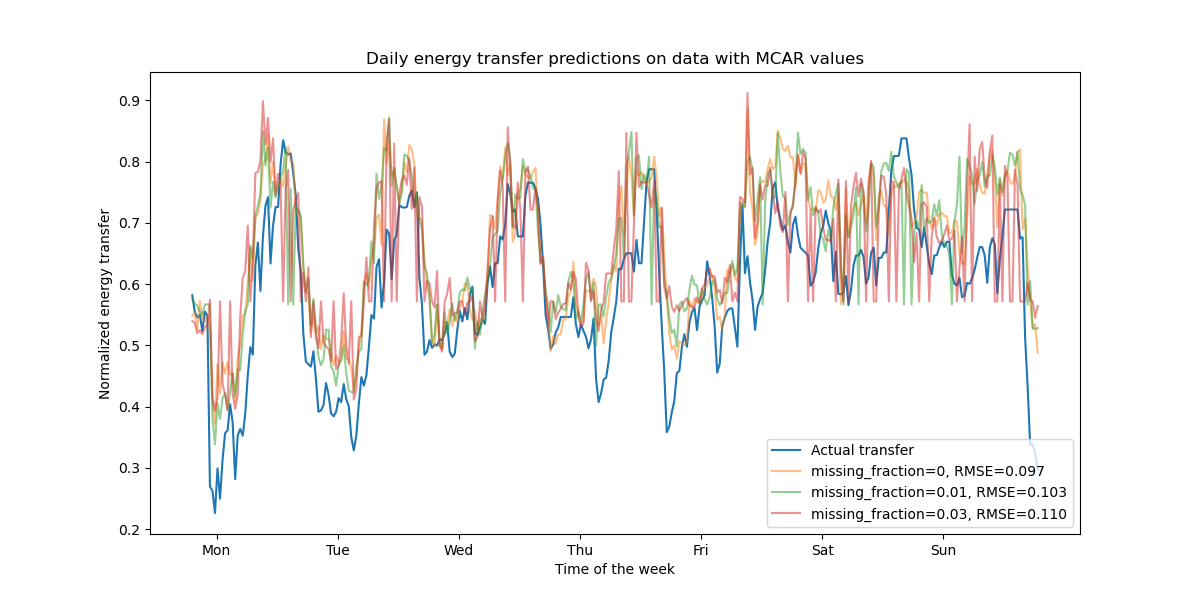
Daily energy transfer predictions on data with MCAR values

Как и ожидалось, качество модели ухудшается с увеличением доли пропущенных значений.

Поддержка квантильной потери#

Квантильная функция потерь в регрессии позволяет оценить изменчивость или неопределенность целевой переменной. Например, прогнозирование 5-го и 95-го процентилей может дать 90% интервал прогнозирования, т.е. диапазон, в котором мы ожидаем, что новое наблюдаемое значение окажется с вероятностью 90%.

from sklearn.metrics import mean_pinball_loss

quantiles = [0.95, 0.05]
predictions = []

fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(y_test.values[first_week], label="Actual transfer")

for quantile in quantiles:
    hgbt_quantile = HistGradientBoostingRegressor(
        loss="quantile", quantile=quantile, **common_params
    )
    hgbt_quantile.fit(X_train, y_train)
    y_pred = hgbt_quantile.predict(X_test[first_week])

    predictions.append(y_pred)
    score = mean_pinball_loss(y_test[first_week], y_pred)
    ax.plot(
        y_pred[first_week],
        label=f"quantile={quantile}, pinball loss={score:.2f}",
        alpha=0.5,
    )

ax.fill_between(
    range(len(predictions[0][first_week])),
    predictions[0][first_week],
    predictions[1][first_week],
    color=colors[0],
    alpha=0.1,
)
ax.set(
    title="Daily energy transfer predictions with quantile loss",
    xticks=[(i + 0.2) * 48 for i in range(7)],
    xticklabels=["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"],
    xlabel="Time of the week",
    ylabel="Normalized energy transfer",
)
_ = ax.legend(loc="lower right")

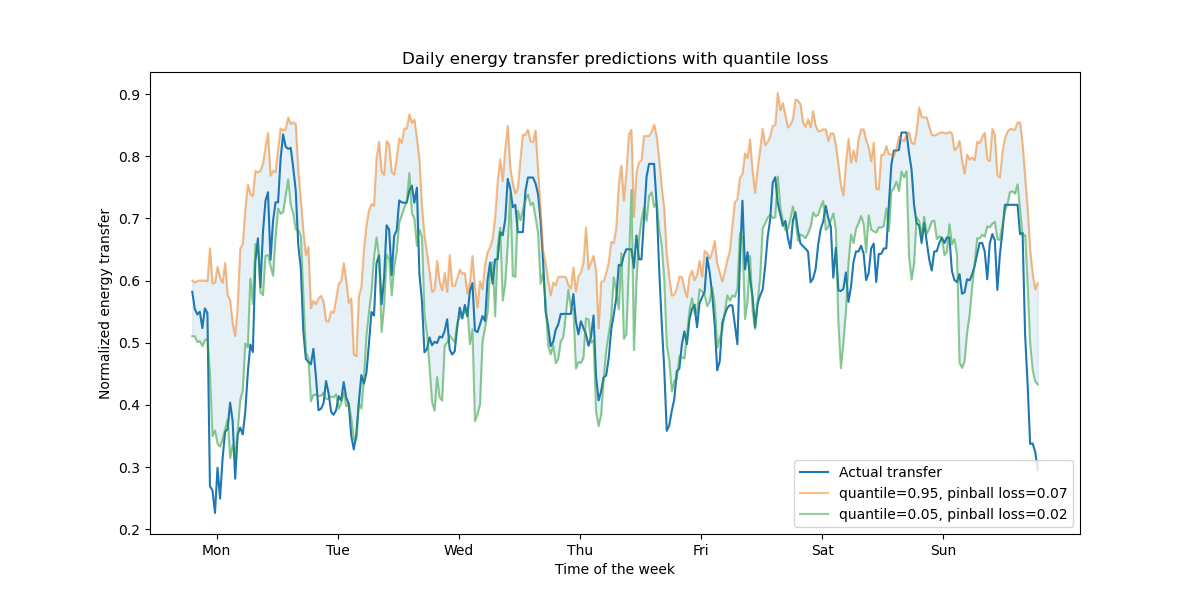
Daily energy transfer predictions with quantile loss

Мы наблюдаем тенденцию к завышению оценки передачи энергии. Это можно количественно подтвердить, вычислив эмпирические показатели покрытия, как это сделано в раздел калибровки доверительных интервалов. Помните, что эти предсказанные процентили являются лишь оценками из модели. Качество таких оценок всё ещё можно улучшить:

сбор большего количества точек данных;
лучшую настройку гиперпараметров модели, см. Интервалы прогнозирования для регрессии градиентного бустинга;
создание более предсказательных признаков из тех же данных, см. Инженерия временных признаков.

Монотонные ограничения#

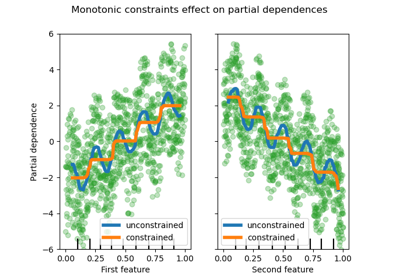
Учитывая специфические знания предметной области, требующие, чтобы связь между признаком и целью была монотонно возрастающей или убывающей, можно обеспечить такое поведение в предсказаниях модели HGBT с помощью монотонных ограничений. Это делает модель более интерпретируемой и может уменьшить её дисперсию (и потенциально смягчить переобучение) за счёт риска увеличения смещения. Монотонные ограничения также можно использовать для обеспечения соответствия специфическим регуляторным требованиям, гарантии соблюдения и соответствия этическим соображениям.

В данном примере политика передачи энергии из Виктории в Новый Южный Уэльс предназначена для смягчения колебаний цен, что означает, что предсказания модели должны обеспечивать такую цель, т.е. передача должна увеличиваться с ростом цены и спроса в Новом Южном Уэльсе, но также уменьшаться с ростом цены и спроса в Виктории, чтобы принести пользу обоим популяциям.

Если обучающие данные имеют имена признаков, можно указать монотонные ограничения, передав словарь с соглашением:

1: монотонное возрастание
0: без ограничений
-1: монотонное уменьшение

В качестве альтернативы можно передать объект, подобный массиву, кодирующий указанное выше соглашение по позиции.

from sklearn.inspection import PartialDependenceDisplay

monotonic_cst = {
    "date": 0,
    "day": 0,
    "period": 0,
    "nswdemand": 1,
    "nswprice": 1,
    "vicdemand": -1,
    "vicprice": -1,
}
hgbt_no_cst = HistGradientBoostingRegressor(
    categorical_features=None, random_state=42
).fit(X, y)
hgbt_cst = HistGradientBoostingRegressor(
    monotonic_cst=monotonic_cst, categorical_features=None, random_state=42
).fit(X, y)

fig, ax = plt.subplots(nrows=2, figsize=(15, 10))
disp = PartialDependenceDisplay.from_estimator(
    hgbt_no_cst,
    X,
    features=["nswdemand", "nswprice"],
    line_kw={"linewidth": 2, "label": "unconstrained", "color": "tab:blue"},
    ax=ax[0],
)
PartialDependenceDisplay.from_estimator(
    hgbt_cst,
    X,
    features=["nswdemand", "nswprice"],
    line_kw={"linewidth": 2, "label": "constrained", "color": "tab:orange"},
    ax=disp.axes_,
)
disp = PartialDependenceDisplay.from_estimator(
    hgbt_no_cst,
    X,
    features=["vicdemand", "vicprice"],
    line_kw={"linewidth": 2, "label": "unconstrained", "color": "tab:blue"},
    ax=ax[1],
)
PartialDependenceDisplay.from_estimator(
    hgbt_cst,
    X,
    features=["vicdemand", "vicprice"],
    line_kw={"linewidth": 2, "label": "constrained", "color": "tab:orange"},
    ax=disp.axes_,
)
_ = plt.legend()

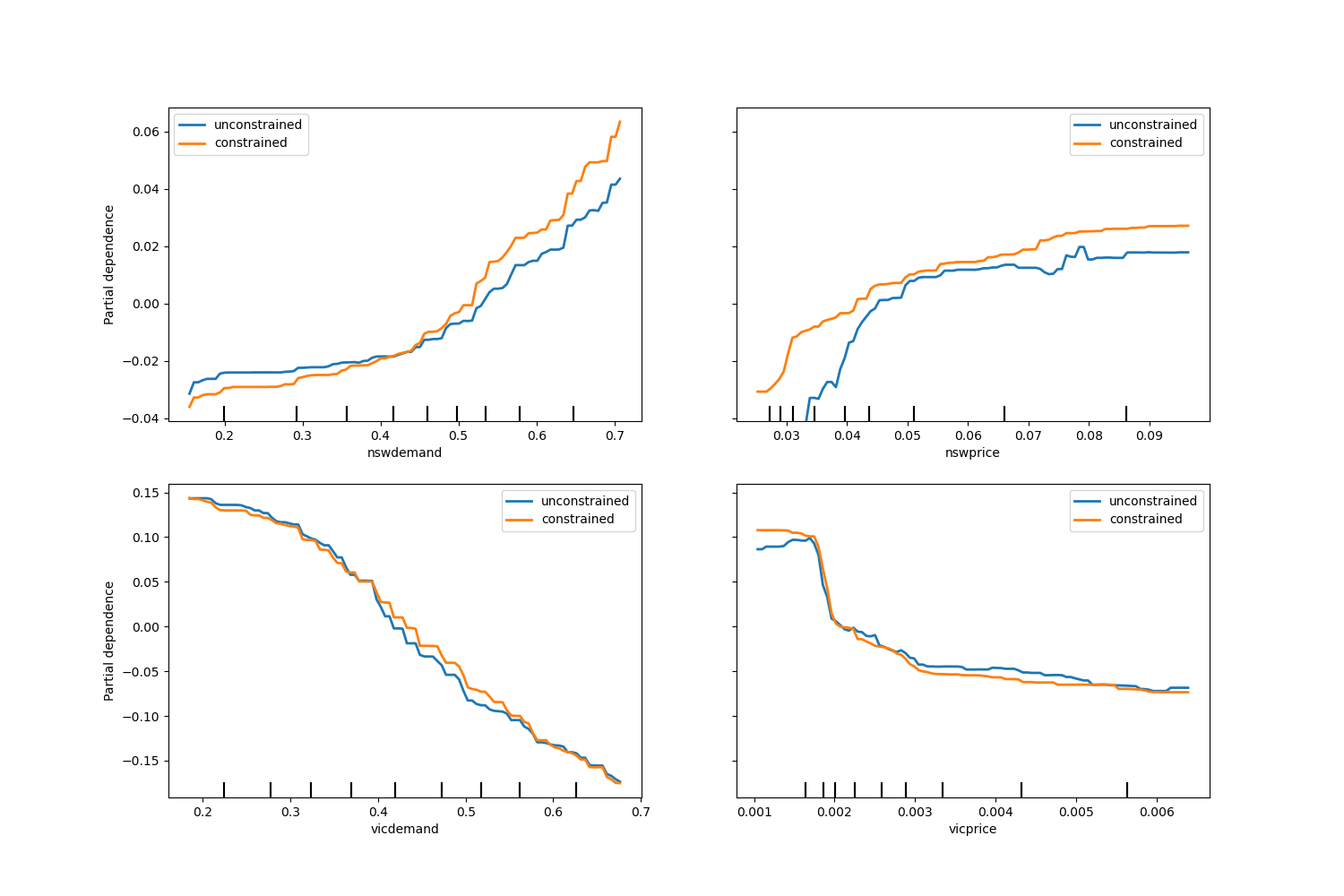
Заметим, что nswdemand и vicdemand уже кажутся монотонными без ограничений. Это хороший пример, показывающий, что модель с ограничениями монотонности является "чрезмерно ограничивающей".

Дополнительно мы можем проверить, что прогностическое качество модели не значительно ухудшается введением монотонных ограничений. Для этой цели мы используем TimeSeriesSplit кросс-валидацию для оценки дисперсии тестовой оценки. Таким образом мы гарантируем, что обучающие данные не предшествуют тестовым, что критически важно при работе с данными, имеющими временную зависимость.

from sklearn.metrics import make_scorer, root_mean_squared_error
from sklearn.model_selection import TimeSeriesSplit, cross_validate

ts_cv = TimeSeriesSplit(n_splits=5, gap=48, test_size=336)  # a week has 336 samples
scorer = make_scorer(root_mean_squared_error)

cv_results = cross_validate(hgbt_no_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE without constraints = {rmse.mean():.3f} +/- {rmse.std():.3f}")

cv_results = cross_validate(hgbt_cst, X, y, cv=ts_cv, scoring=scorer)
rmse = cv_results["test_score"]
print(f"RMSE with constraints    = {rmse.mean():.3f} +/- {rmse.std():.3f}")

RMSE without constraints = 0.103 +/- 0.030
RMSE with constraints    = 0.107 +/- 0.034

Тем не менее, обратите внимание, что сравнение проводится между двумя разными моделями, которые могут быть оптимизированы разной комбинацией гиперпараметров. Это причина, по которой мы не используем common_params в этом разделе, как делалось ранее.

Общее время выполнения скрипта: (0 минут 20.613 секунд)