Монотонные ограничения

Этот пример иллюстрирует влияние монотонных ограничений на градиентный бустинговый оценщик.

Мы строим искусственный набор данных, где целевое значение в целом положительно коррелирует с первым признаком (с некоторыми случайными и неслучайными вариациями), и в целом отрицательно коррелирует со вторым признаком.

Путем наложения ограничения монотонного возрастания или монотонного убывания соответственно на признаки в процессе обучения, оценщик способен правильно следовать общему тренду вместо того, чтобы подвергаться вариациям.

Этот пример был вдохновлён Документация XGBoost.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.inspection import PartialDependenceDisplay

rng = np.random.RandomState(0)

n_samples = 1000
f_0 = rng.rand(n_samples)
f_1 = rng.rand(n_samples)
X = np.c_[f_0, f_1]
noise = rng.normal(loc=0.0, scale=0.01, size=n_samples)

# y is positively correlated with f_0, and negatively correlated with f_1
y = 5 * f_0 + np.sin(10 * np.pi * f_0) - 5 * f_1 - np.cos(10 * np.pi * f_1) + noise

Обучите первую модель на этом наборе данных без ограничений.

gbdt_no_cst = HistGradientBoostingRegressor()
gbdt_no_cst.fit(X, y)

HistGradientBoostingRegressor()

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Обучите вторую модель на этом наборе данных с ограничениями монотонного увеличения (1) и монотонного уменьшения (-1) соответственно.

gbdt_with_monotonic_cst = HistGradientBoostingRegressor(monotonic_cst=[1, -1])
gbdt_with_monotonic_cst.fit(X, y)

HistGradientBoostingRegressor(monotonic_cst=[1, -1])

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Давайте отобразим частичную зависимость предсказаний от двух признаков.

fig, ax = plt.subplots()
disp = PartialDependenceDisplay.from_estimator(
    gbdt_no_cst,
    X,
    features=[0, 1],
    feature_names=(
        "First feature",
        "Second feature",
    ),
    line_kw={"linewidth": 4, "label": "unconstrained", "color": "tab:blue"},
    ax=ax,
)
PartialDependenceDisplay.from_estimator(
    gbdt_with_monotonic_cst,
    X,
    features=[0, 1],
    line_kw={"linewidth": 4, "label": "constrained", "color": "tab:orange"},
    ax=disp.axes_,
)

for f_idx in (0, 1):
    disp.axes_[0, f_idx].plot(
        X[:, f_idx], y, "o", alpha=0.3, zorder=-1, color="tab:green"
    )
    disp.axes_[0, f_idx].set_ylim(-6, 6)

plt.legend()
fig.suptitle("Monotonic constraints effect on partial dependences")
plt.show()

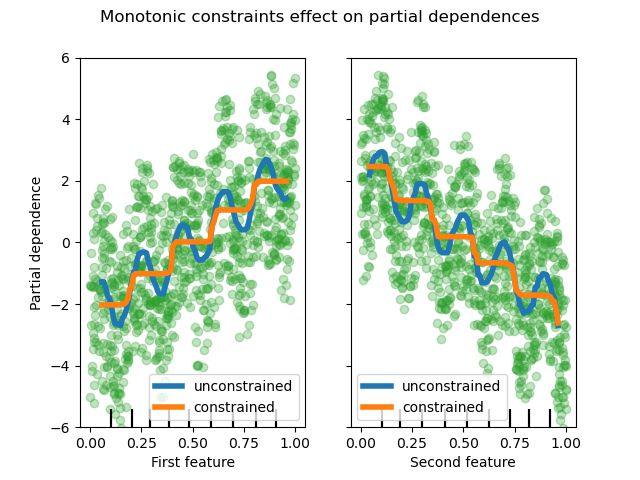
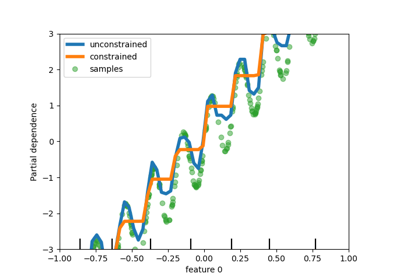
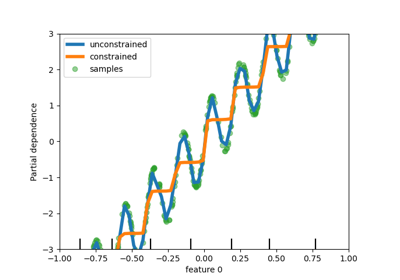
Мы видим, что прогнозы неограниченной модели улавливают колебания данных, в то время как ограниченная модель следует общему тренду и игнорирует локальные вариации.

Использование имен признаков для указания монотонных ограничений

Обратите внимание, что если обучающие данные имеют имена признаков, можно указать монотонные ограничения, передав словарь:

import pandas as pd

X_df = pd.DataFrame(X, columns=["f_0", "f_1"])

gbdt_with_monotonic_cst_df = HistGradientBoostingRegressor(
    monotonic_cst={"f_0": 1, "f_1": -1}
).fit(X_df, y)

np.allclose(
    gbdt_with_monotonic_cst_df.predict(X_df), gbdt_with_monotonic_cst.predict(X)
)

True

Связанные примеры

Основные новости выпуска scikit-learn 0.23

Основные новости выпуска scikit-learn 0.23

Основные нововведения выпуска scikit-learn 1.4

Основные нововведения выпуска scikit-learn 1.4

Признаки в деревьях с градиентным бустингом на гистограммах

Признаки в деревьях с градиентным бустингом на гистограммах

Расширенное построение графиков с частичной зависимостью

Расширенное построение графиков с частичной зависимостью