Визуализация вероятностных предсказаний VotingClassifier

Постройте предсказанные вероятности классов в игрушечном наборе данных, предсказанные тремя разными классификаторами и усредненные с помощью VotingClassifier.

Сначала инициализируются три линейных классификатора. Два из них - сплайновые модели с членами взаимодействия, один использует постоянную экстраполяцию, а другой - периодическую экстраполяцию. Третий классификатор - это Nystroem с ядром по умолчанию "rbf".

В первой части этого примера эти три классификатора используются для демонстрации мягкого голосования с использованием VotingClassifier со взвешенным средним. Мы устанавливаем weights=[2, 1, 3], что означает, что предсказания модели сплайна с постоянной экстраполяцией взвешиваются в два раза больше, чем предсказания модели периодического сплайна, а предсказания модели Nystroem взвешиваются в три раза больше, чем предсказания периодического сплайна.

Вторая часть демонстрирует, как мягкие прогнозы могут быть преобразованы в жесткие прогнозы.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Сначала мы генерируем зашумленный набор данных XOR, который представляет собой задачу бинарной классификации.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from matplotlib.colors import ListedColormap

n_samples = 500
rng = np.random.default_rng(0)
feature_names = ["Feature #0", "Feature #1"]
common_scatter_plot_params = dict(
    cmap=ListedColormap(["tab:red", "tab:blue"]),
    edgecolor="white",
    linewidth=1,
)

xor = pd.DataFrame(
    np.random.RandomState(0).uniform(low=-1, high=1, size=(n_samples, 2)),
    columns=feature_names,
)
noise = rng.normal(loc=0, scale=0.1, size=(n_samples, 2))
target_xor = np.logical_xor(
    xor["Feature #0"] + noise[:, 0] > 0, xor["Feature #1"] + noise[:, 1] > 0
)

X = xor[feature_names]
y = target_xor.astype(np.int32)

fig, ax = plt.subplots()
ax.scatter(X["Feature #0"], X["Feature #1"], c=y, **common_scatter_plot_params)
ax.set_title("The XOR dataset")
plt.show()

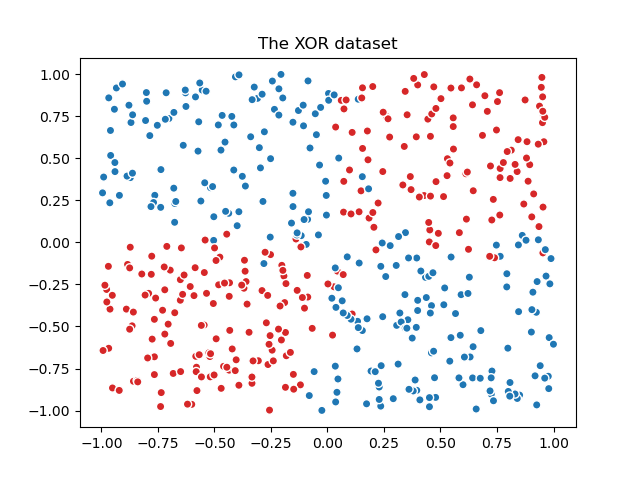
Из-за присущей нелинейной разделимости набора данных XOR модели на основе деревьев часто предпочтительнее. Однако соответствующая инженерия признаков в сочетании с линейной моделью может дать эффективные результаты, с дополнительным преимуществом получения лучше калиброванных вероятностей для образцов, расположенных в переходных областях, подверженных шуму.

Мы определяем и обучаем модели на всём наборе данных.

from sklearn.ensemble import VotingClassifier
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, SplineTransformer, StandardScaler

clf1 = make_pipeline(
    SplineTransformer(degree=2, n_knots=2),
    PolynomialFeatures(interaction_only=True),
    LogisticRegression(C=10),
)
clf2 = make_pipeline(
    SplineTransformer(
        degree=2,
        n_knots=4,
        extrapolation="periodic",
        include_bias=True,
    ),
    PolynomialFeatures(interaction_only=True),
    LogisticRegression(C=10),
)
clf3 = make_pipeline(
    StandardScaler(),
    Nystroem(gamma=2, random_state=0),
    LogisticRegression(C=10),
)
weights = [2, 1, 3]
eclf = VotingClassifier(
    estimators=[
        ("constant splines model", clf1),
        ("periodic splines model", clf2),
        ("nystroem model", clf3),
    ],
    voting="soft",
    weights=weights,
)

clf1.fit(X, y)
clf2.fit(X, y)
clf3.fit(X, y)
eclf.fit(X, y)

VotingClassifier(estimators=[('constant splines model',
                              Pipeline(steps=[('splinetransformer',
                                               SplineTransformer(degree=2,
                                                                 n_knots=2)),
                                              ('polynomialfeatures',
                                               PolynomialFeatures(interaction_only=True)),
                                              ('logisticregression',
                                               LogisticRegression(C=10))])),
                             ('periodic splines model',
                              Pipeline(steps=[('splinetransformer',
                                               SplineTransformer(degree=2,
                                                                 extrapolation='periodic',
                                                                 n_knots=4)),
                                              ('polynomialfeatures',
                                               PolynomialFeatures(interaction_only=True)),
                                              ('logisticregression',
                                               LogisticRegression(C=10))])),
                             ('nystroem model',
                              Pipeline(steps=[('standardscaler',
                                               StandardScaler()),
                                              ('nystroem',
                                               Nystroem(gamma=2,
                                                        random_state=0)),
                                              ('logisticregression',
                                               LogisticRegression(C=10))]))],
                 voting='soft', weights=[2, 1, 3])

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

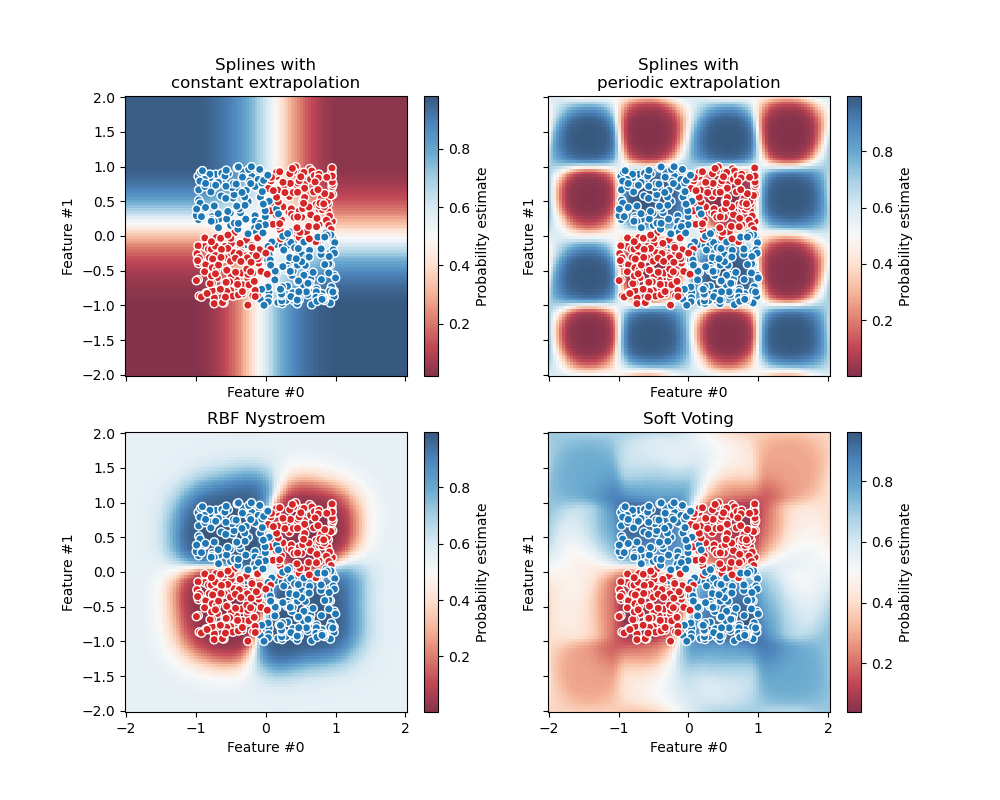
Наконец, мы используем DecisionBoundaryDisplay для построения предсказанных вероятностей. Используя расходящуюся цветовую карту (такую как "RdBu"), мы можем гарантировать, что более темные цвета соответствуют predict_proba близко к 0 или 1, а белый соответствует predict_proba 0.5.

from itertools import product

from sklearn.inspection import DecisionBoundaryDisplay

fig, axarr = plt.subplots(2, 2, sharex="col", sharey="row", figsize=(10, 8))
for idx, clf, title in zip(
    product([0, 1], [0, 1]),
    [clf1, clf2, clf3, eclf],
    [
        "Splines with\nconstant extrapolation",
        "Splines with\nperiodic extrapolation",
        "RBF Nystroem",
        "Soft Voting",
    ],
):
    disp = DecisionBoundaryDisplay.from_estimator(
        clf,
        X,
        response_method="predict_proba",
        plot_method="pcolormesh",
        cmap="RdBu",
        alpha=0.8,
        ax=axarr[idx[0], idx[1]],
    )
    axarr[idx[0], idx[1]].scatter(
        X["Feature #0"],
        X["Feature #1"],
        c=y,
        **common_scatter_plot_params,
    )
    axarr[idx[0], idx[1]].set_title(title)
    fig.colorbar(disp.surface_, ax=axarr[idx[0], idx[1]], label="Probability estimate")

plt.show()

В качестве проверки мы можем убедиться для заданной выборки, что вероятность, предсказанная VotingClassifier действительно является взвешенным средним мягких предсказаний отдельных классификаторов.

В случае бинарной классификации, как в данном примере, predict_proba массивы содержат вероятность принадлежности к классу 0 (здесь красным) как первую запись, и вероятность принадлежности к классу 1 (здесь синим) как вторую запись.

test_sample = pd.DataFrame({"Feature #0": [-0.5], "Feature #1": [1.5]})
predict_probas = [est.predict_proba(test_sample).ravel() for est in eclf.estimators_]
for (est_name, _), est_probas in zip(eclf.estimators, predict_probas):
    print(f"{est_name}'s predicted probabilities: {est_probas}")

constant splines model's predicted probabilities: [0.11272662 0.88727338]
periodic splines model's predicted probabilities: [0.99726573 0.00273427]
nystroem model's predicted probabilities: [0.3185838 0.6814162]

print(
    "Weighted average of soft-predictions: "
    f"{np.dot(weights, predict_probas) / np.sum(weights)}"
)

Weighted average of soft-predictions: [0.3630784 0.6369216]

Мы видим, что ручной расчет предсказанных вероятностей выше эквивалентен тому, что производится VotingClassifier:

print(
    "Predicted probability of VotingClassifier: "
    f"{eclf.predict_proba(test_sample).ravel()}"
)

Predicted probability of VotingClassifier: [0.3630784 0.6369216]

Чтобы преобразовать мягкие предсказания в жесткие при наличии весов, вычисляются взвешенные средние предсказанные вероятности для каждого класса. Затем итоговая метка класса выводится из метки класса с наибольшей средней вероятностью, что соответствует порогу по умолчанию на predict_proba=0.5 в случае бинарной классификации.

print(
    "Class with the highest weighted average of soft-predictions: "
    f"{np.argmax(np.dot(weights, predict_probas) / np.sum(weights))}"
)

Class with the highest weighted average of soft-predictions: 1

Это эквивалентно выводу VotingClassifier’s predict method:

print(f"Predicted class of VotingClassifier: {eclf.predict(test_sample).ravel()}")

Predicted class of VotingClassifier: [1]

Мягкие голоса могут быть пороговыми, как и для любого другого вероятностного классификатора. Это позволяет установить пороговую вероятность, при которой будет предсказан положительный класс, вместо простого выбора класса с наибольшей предсказанной вероятностью.

from sklearn.model_selection import FixedThresholdClassifier

eclf_other_threshold = FixedThresholdClassifier(
    eclf, threshold=0.7, response_method="predict_proba"
).fit(X, y)
print(
    "Predicted class of thresholded VotingClassifier: "
    f"{eclf_other_threshold.predict(test_sample)}"
)

Predicted class of thresholded VotingClassifier: [0]

Связанные примеры

Построить график вероятности классификации

Построить график вероятности классификации

Полиномиальная и сплайновая интерполяция

Полиномиальная и сплайновая интерполяция

Сравнение калибровки классификаторов

Сравнение калибровки классификаторов

Граница решения полуконтролируемых классификаторов против SVM на наборе данных Iris

Граница решения полуконтролируемых классификаторов против SVM на наборе данных Iris