Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Градиентный бустинг для регрессии#
Этот пример демонстрирует градиентный бустинг для создания прогнозной модели из ансамбля слабых прогнозных моделей. Градиентный бустинг можно использовать для задач регрессии и классификации. Здесь мы обучим модель для решения задачи регрессии по диабету. Мы получим результаты из
GradientBoostingRegressor с наименьшими квадратами потерь и 500 регрессионными деревьями глубины 4.
Примечание: Для больших наборов данных (n_samples >= 10000) обратитесь к
HistGradientBoostingRegressor. См.
Признаки в деревьях с градиентным бустингом на гистограммах для примера,
демонстрирующего некоторые другие преимущества
HistGradientBoostingRegressor.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, ensemble
from sklearn.inspection import permutation_importance
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.utils.fixes import parse_version
Загрузить данные#
Сначала нам нужно загрузить данные.
diabetes = datasets.load_diabetes()
X, y = diabetes.data, diabetes.target
Предобработка данных#
Далее мы разделим наш набор данных, используя 90% для обучения и оставив остальное для тестирования. Мы также установим параметры модели регрессии. Вы можете поэкспериментировать с этими параметрами, чтобы увидеть, как изменяются результаты.
n_estimators : количество этапов бустинга, которые будут выполнены.
Позже мы построим график девиации в зависимости от итераций бустинга.
max_depth : ограничивает количество узлов в дереве.
Лучшее значение зависит от взаимодействия входных переменных.
min_samples_split : минимальное количество образцов, необходимое для разделения внутреннего узла.
learning_rate : насколько будет уменьшен вклад каждого дерева.
loss : функция потерь для оптимизации. В данном случае используется функция наименьших квадратов, однако есть много других вариантов (см.
GradientBoostingRegressor ).
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.1, random_state=13
)
params = {
"n_estimators": 500,
"max_depth": 4,
"min_samples_split": 5,
"learning_rate": 0.01,
"loss": "squared_error",
}
Обучить модель регрессии#
Теперь мы инициируем регрессоры градиентного бустинга и обучим их на наших обучающих данных. Давайте также посмотрим на среднеквадратичную ошибку на тестовых данных.
reg = ensemble.GradientBoostingRegressor(**params)
reg.fit(X_train, y_train)
mse = mean_squared_error(y_test, reg.predict(X_test))
print("The mean squared error (MSE) on test set: {:.4f}".format(mse))
The mean squared error (MSE) on test set: 3010.2061
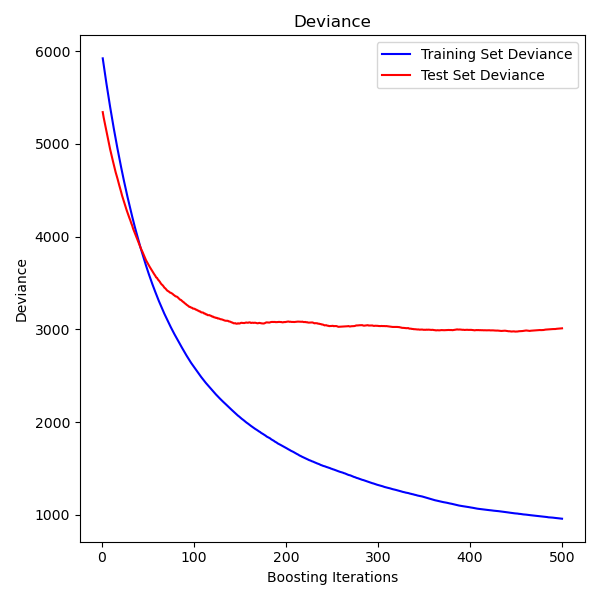
Построение отклонения при обучении#
Наконец, мы визуализируем результаты. Для этого сначала вычислим отклонение тестового набора, а затем построим график в зависимости от итераций бустинга.
test_score = np.zeros((params["n_estimators"],), dtype=np.float64)
for i, y_pred in enumerate(reg.staged_predict(X_test)):
test_score[i] = mean_squared_error(y_test, y_pred)
fig = plt.figure(figsize=(6, 6))
plt.subplot(1, 1, 1)
plt.title("Deviance")
plt.plot(
np.arange(params["n_estimators"]) + 1,
reg.train_score_,
"b-",
label="Training Set Deviance",
)
plt.plot(
np.arange(params["n_estimators"]) + 1, test_score, "r-", label="Test Set Deviance"
)
plt.legend(loc="upper right")
plt.xlabel("Boosting Iterations")
plt.ylabel("Deviance")
fig.tight_layout()
plt.show()
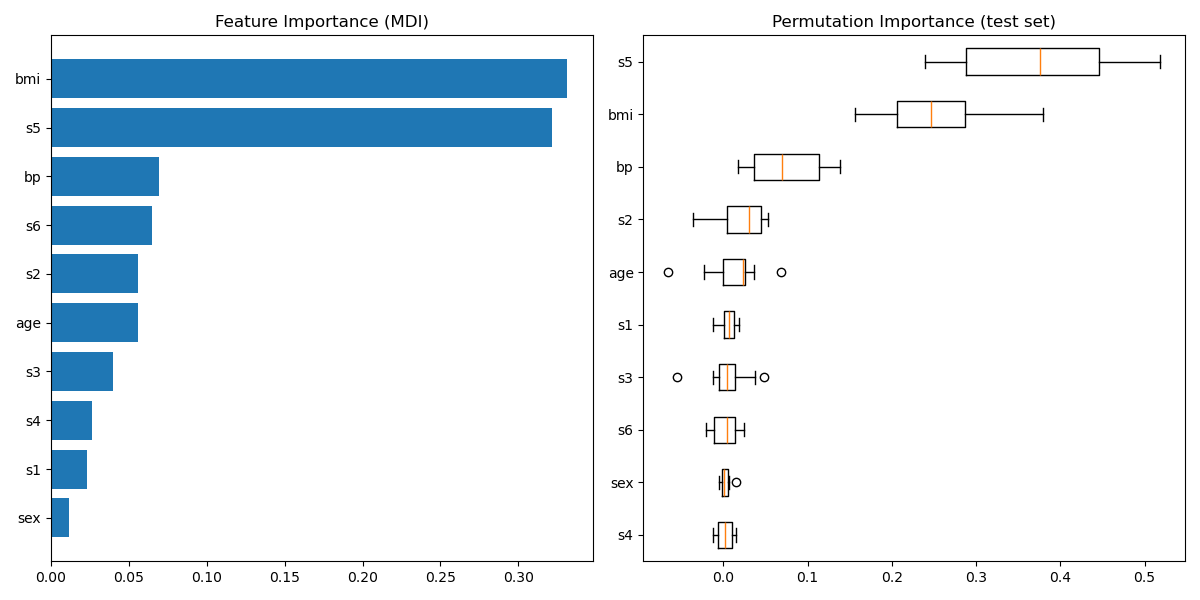
Построить важность признаков#
Предупреждение
Внимание, важность признаков на основе нечистоты может вводить в заблуждение для
высокая кардинальность признаков (много уникальных значений). В качестве альтернативы,
перестановочные важности reg может быть вычислен на
отложенном тестовом наборе. См. Важность признаков на основе перестановок для получения дополнительной информации.
В этом примере методы на основе нечистоты и перестановки идентифицируют те же 2 сильно предсказательных признака, но не в том же порядке. Третий наиболее предсказательный признак, "bp", также одинаков для обоих методов. Остальные признаки менее предсказательны, и полосы ошибок на графике перестановок показывают, что они перекрываются с 0.
feature_importance = reg.feature_importances_
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5
fig = plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.barh(pos, feature_importance[sorted_idx], align="center")
plt.yticks(pos, np.array(diabetes.feature_names)[sorted_idx])
plt.title("Feature Importance (MDI)")
result = permutation_importance(
reg, X_test, y_test, n_repeats=10, random_state=42, n_jobs=2
)
sorted_idx = result.importances_mean.argsort()
plt.subplot(1, 2, 2)
# `labels` argument in boxplot is deprecated in matplotlib 3.9 and has been
# renamed to `tick_labels`. The following code handles this, but as a
# scikit-learn user you probably can write simpler code by using `labels=...`
# (matplotlib < 3.9) or `tick_labels=...` (matplotlib >= 3.9).
tick_labels_parameter_name = (
"tick_labels"
if parse_version(matplotlib.__version__) >= parse_version("3.9")
else "labels"
)
tick_labels_dict = {
tick_labels_parameter_name: np.array(diabetes.feature_names)[sorted_idx]
}
plt.boxplot(result.importances[sorted_idx].T, vert=False, **tick_labels_dict)
plt.title("Permutation Importance (test set)")
fig.tight_layout()
plt.show()
Общее время выполнения скрипта: (0 минут 1.247 секунд)
Связанные примеры
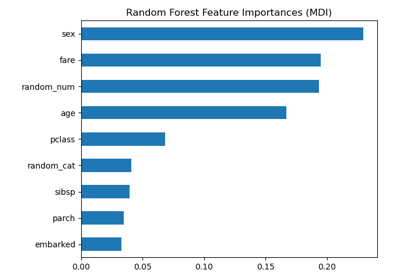
Важность перестановок против важности признаков случайного леса (MDI)
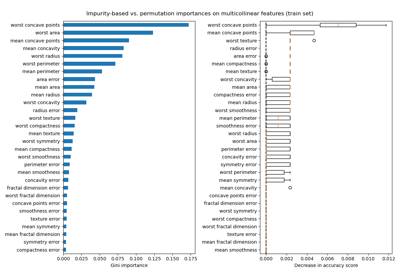
Важность перестановок с мультиколлинеарными или коррелированными признаками