Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Многоклассовые деревья решений с бустингом AdaBoost#

Этот пример показывает, как бустинг может улучшить точность предсказания в задаче многоклассовой классификации. Он воспроизводит аналогичный эксперимент, изображенный на Рисунке 1 в Zhu et al [1].

Основной принцип AdaBoost (адаптивного бустинга) — обучение последовательности слабых алгоритмов (например, деревьев решений) на повторно перевыбираемых версиях данных. Каждая выборка имеет вес, который корректируется после каждого шага обучения, так что неправильно классифицированным выборкам присваиваются более высокие веса. Процесс повторной выборки с возвращением учитывает веса, назначенные каждой выборке. Выборки с более высокими весами имеют больше шансов быть выбранными несколько раз в новом наборе данных, в то время как выборки с меньшими весами менее вероятны. Это гарантирует, что последующие итерации алгоритма фокусируются на трудно классифицируемых выборках.

Ссылки

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Создание набора данных#

Классификационный набор данных строится путём взятия десятимерного стандартного нормального распределения (\(x\) в \(R^{10}\)) и определения трех классов, разделенных вложенными концентрическими десятимерными сферами, так что примерно равное количество выборок находится в каждом классе (квантили \(\chi^2\) распределение).

from sklearn.datasets import make_gaussian_quantiles

X, y = make_gaussian_quantiles(
    n_samples=2_000, n_features=10, n_classes=3, random_state=1
)

Мы разделяем набор данных на 2 части: 70 процентов выборок используются для обучения, а оставшиеся 30 процентов — для тестирования.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(
    X, y, train_size=0.7, random_state=42
)

Обучение `AdaBoostClassifier`#

Мы обучаем AdaBoostClassifier. Оценщик использует бустинг для повышения точности классификации. Бустинг — это метод, предназначенный для обучения слабых учеников (т.е. estimator), которые учатся на ошибках своих предшественников.

Здесь мы определяем слабый классификатор как DecisionTreeClassifier и установить максимальное количество листьев равным 8. В реальной настройке этот параметр следует настраивать. Мы устанавливаем его на довольно низкое значение, чтобы ограничить время выполнения примера.

The SAMME алгоритм, встроенный в AdaBoostClassifier затем использует правильные или неправильные предсказания, сделанные текущим слабым учеником, для обновления весов образцов, используемых для обучения последующих слабых учеников. Также вес самого слабого ученика рассчитывается на основе его точности в классификации обучающих примеров. Вес слабого ученика определяет его влияние на окончательное предсказание ансамбля.

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier

weak_learner = DecisionTreeClassifier(max_leaf_nodes=8)
n_estimators = 300

adaboost_clf = AdaBoostClassifier(
    estimator=weak_learner,
    n_estimators=n_estimators,
    random_state=42,
).fit(X_train, y_train)

Анализ#

Сходимость `AdaBoostClassifier`#

Чтобы продемонстрировать эффективность бустинга в улучшении точности, мы оцениваем ошибку классификации бустированных деревьев в сравнении с двумя базовыми оценками. Первая базовая оценка - это misclassification_error полученный от одного слабого обучающегося (т.е. DecisionTreeClassifier), который служит контрольной точкой. Второй базовый результат получен из DummyClassifier, который предсказывает наиболее распространенный класс в наборе данных.

from sklearn.dummy import DummyClassifier
from sklearn.metrics import accuracy_score

dummy_clf = DummyClassifier()


def misclassification_error(y_true, y_pred):
    return 1 - accuracy_score(y_true, y_pred)


weak_learners_misclassification_error = misclassification_error(
    y_test, weak_learner.fit(X_train, y_train).predict(X_test)
)

dummy_classifiers_misclassification_error = misclassification_error(
    y_test, dummy_clf.fit(X_train, y_train).predict(X_test)
)

print(
    "DecisionTreeClassifier's misclassification_error: "
    f"{weak_learners_misclassification_error:.3f}"
)
print(
    "DummyClassifier's misclassification_error: "
    f"{dummy_classifiers_misclassification_error:.3f}"
)

DecisionTreeClassifier's misclassification_error: 0.475
DummyClassifier's misclassification_error: 0.692

После обучения DecisionTreeClassifier модели, достигнутая ошибка превышает ожидаемое значение, которое было бы получено при угадывании наиболее частого метки класса, так как DummyClassifier делает.

Теперь мы вычисляем misclassification_error, т.е. 1 - accuracy, аддитивной модели (DecisionTreeClassifier) на каждой итерации бустинга на тестовом наборе для оценки его производительности.

Мы используем staged_predict , который выполняет столько итераций, сколько обученных оценщиков (т.е. соответствует n_estimators). На итерации n, предсказания AdaBoost используют только n первых слабых учеников. Мы сравниваем эти предсказания с истинными предсказаниями y_test и, следовательно, мы делаем вывод о пользе (или её отсутствии) добавления нового слабого обучающегося в цепочку.

Мы отображаем ошибку неправильной классификации для различных этапов:

import matplotlib.pyplot as plt
import pandas as pd

boosting_errors = pd.DataFrame(
    {
        "Number of trees": range(1, n_estimators + 1),
        "AdaBoost": [
            misclassification_error(y_test, y_pred)
            for y_pred in adaboost_clf.staged_predict(X_test)
        ],
    }
).set_index("Number of trees")
ax = boosting_errors.plot()
ax.set_ylabel("Misclassification error on test set")
ax.set_title("Convergence of AdaBoost algorithm")

plt.plot(
    [boosting_errors.index.min(), boosting_errors.index.max()],
    [weak_learners_misclassification_error, weak_learners_misclassification_error],
    color="tab:orange",
    linestyle="dashed",
)
plt.plot(
    [boosting_errors.index.min(), boosting_errors.index.max()],
    [
        dummy_classifiers_misclassification_error,
        dummy_classifiers_misclassification_error,
    ],
    color="c",
    linestyle="dotted",
)
plt.legend(["AdaBoost", "DecisionTreeClassifier", "DummyClassifier"], loc=1)
plt.show()

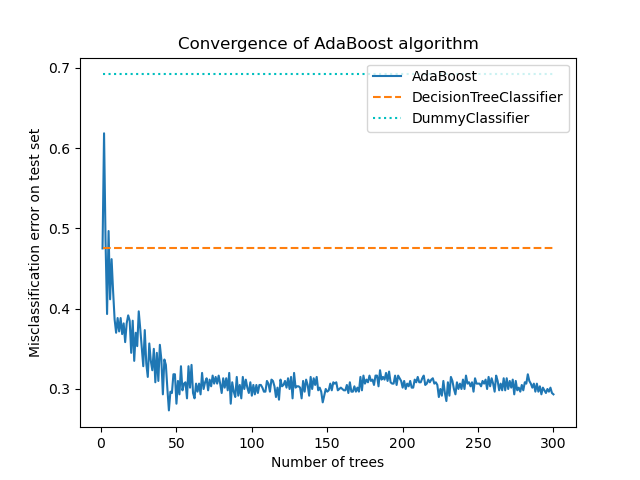
График показывает ошибку неправильной классификации на тестовом наборе после каждой итерации бустинга. Мы видим, что ошибка бустированных деревьев сходится к ошибке около 0.3 после 50 итераций, что указывает на значительно более высокую точность по сравнению с одним деревом, как показано пунктирной линией на графике.

Ошибка неправильной классификации колеблется, потому что SAMME алгоритм использует дискретные выходы слабых обучающихся для обучения бустинговой модели.

Сходимость AdaBoostClassifier в основном зависит от скорости обучения (т.е. learning_rate), количество используемых слабых обучаемых (n_estimators), и выразительность слабых обучаемых моделей (например, max_leaf_nodes).

Ошибки и веса слабых обучающих алгоритмов#

Как упоминалось ранее, AdaBoost — это аддитивная модель с последовательным добавлением. Теперь мы сосредоточимся на понимании взаимосвязи между присвоенными весами слабых обучающих алгоритмов и их статистической производительностью.

Мы используем обученный AdaBoostClassifierатрибуты estimator_errors_ и estimator_weights_ для исследования этой связи.

weak_learners_info = pd.DataFrame(
    {
        "Number of trees": range(1, n_estimators + 1),
        "Errors": adaboost_clf.estimator_errors_,
        "Weights": adaboost_clf.estimator_weights_,
    }
).set_index("Number of trees")

axs = weak_learners_info.plot(
    subplots=True, layout=(1, 2), figsize=(10, 4), legend=False, color="tab:blue"
)
axs[0, 0].set_ylabel("Train error")
axs[0, 0].set_title("Weak learner's training error")
axs[0, 1].set_ylabel("Weight")
axs[0, 1].set_title("Weak learner's weight")
fig = axs[0, 0].get_figure()
fig.suptitle("Weak learner's errors and weights for the AdaBoostClassifier")
fig.tight_layout()

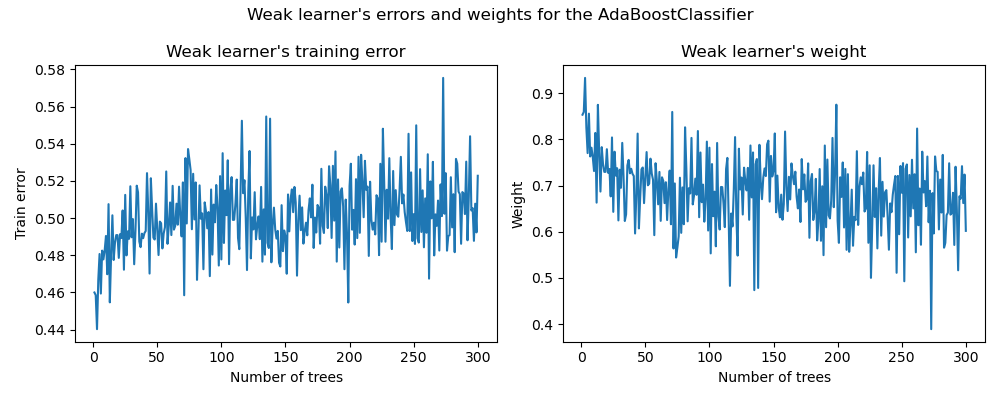
Weak learner's errors and weights for the AdaBoostClassifier, Weak learner's training error, Weak learner's weight

На левом графике показана взвешенная ошибка каждого слабого обучающегося на перевзвешенном обучающем наборе на каждой итерации бустинга. На правом графике показаны веса, связанные с каждым слабым обучающимся, которые позже используются для предсказаний итоговой аддитивной модели.

Мы видим, что ошибка слабого обучающегося обратна весам. Это означает, что наша аддитивная модель будет больше доверять слабому обучающемуся, который делает меньшие ошибки (на обучающей выборке), увеличивая его влияние на окончательное решение. Действительно, это именно формулировка обновления весов базовых оценщиков после каждой итерации в AdaBoost.

Еще одно интересное наблюдение сводится к тому, что первые слабые ученики модели допускают меньше ошибок, чем более поздние слабые ученики в цепочке бустинга.

Интуиция, стоящая за этим наблюдением, следующая: из-за перевзвешивания выборки последующие классификаторы вынуждены пытаться классифицировать более сложные или зашумленные образцы и игнорировать уже хорошо классифицированные образцы. Поэтому, общая ошибка на обучающем наборе будет увеличиваться. Вот почему веса слабых учеников построены так, чтобы уравновешивать худшие слабые ученики.

Общее время выполнения скрипта: (0 минут 3.826 секунд)