Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Интервалы прогнозирования для регрессии градиентного бустинга#
Этот пример показывает, как квантильная регрессия может использоваться для создания интервалов прогнозирования. См. Признаки в деревьях с градиентным бустингом на гистограммах
для примера, демонстрирующего некоторые другие возможности
HistGradientBoostingRegressor.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Сгенерировать некоторые данные для синтетической задачи регрессии, применяя функцию f к равномерно выбранным случайным входам.
import numpy as np
from sklearn.model_selection import train_test_split
def f(x):
"""The function to predict."""
return x * np.sin(x)
rng = np.random.RandomState(42)
X = np.atleast_2d(rng.uniform(0, 10.0, size=1000)).T
expected_y = f(X).ravel()
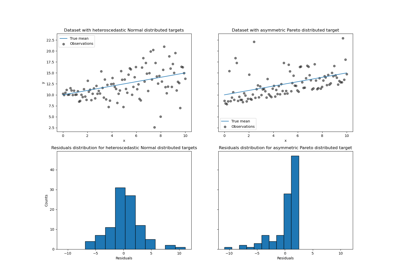
Выбрать 10 наиболее неопределенных меток лог-нормальное. Чтобы сделать это ещё интереснее, мы рассматриваем случай, когда амплитуда шума зависит от входной переменной x (гетероскедастичный шум).
Логнормальное распределение несимметрично и имеет длинный хвост: наблюдение больших выбросов вероятно, но невозможно наблюдать малые выбросы.
sigma = 0.5 + X.ravel() / 10
noise = rng.lognormal(sigma=sigma) - np.exp(sigma**2 / 2)
y = expected_y + noise
Разделить на обучающий и тестовый наборы данных:
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Обучение нелинейных квантильных регрессоров и регрессоров методом наименьших квадратов#
Обучите модели градиентного бустинга с функцией потерь квантиля и alpha=0.05, 0.5, 0.95.
Модели, полученные для alpha=0.05 и alpha=0.95, дают 90% доверительный интервал (95% - 5% = 90%).
Модель, обученная с alpha=0.5, дает регрессию медианы: в среднем должно быть одинаковое количество целевых наблюдений выше и ниже предсказанных значений.
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_pinball_loss, mean_squared_error
all_models = {}
common_params = dict(
learning_rate=0.05,
n_estimators=200,
max_depth=2,
min_samples_leaf=9,
min_samples_split=9,
)
for alpha in [0.05, 0.5, 0.95]:
gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, **common_params)
all_models["q %1.2f" % alpha] = gbr.fit(X_train, y_train)
Обратите внимание, что HistGradientBoostingRegressor значительно быстрее, чем GradientBoostingRegressor начиная с промежуточных наборов данных (n_samples >= 10_000), что не относится к данному примеру.
Для сравнения мы также обучаем базовую модель с использованием обычной среднеквадратичной ошибки (MSE).
gbr_ls = GradientBoostingRegressor(loss="squared_error", **common_params)
all_models["mse"] = gbr_ls.fit(X_train, y_train)
Создание равномерно распределенного набора входных значений в диапазоне [0, 10].
xx = np.atleast_2d(np.linspace(0, 10, 1000)).T
Постройте истинную функцию условного среднего f, предсказания условного среднего (потери равны квадрату ошибки), условной медианы и условного 90% интервала (от 5-го до 95-го условных процентилей).
import matplotlib.pyplot as plt
y_pred = all_models["mse"].predict(xx)
y_lower = all_models["q 0.05"].predict(xx)
y_upper = all_models["q 0.95"].predict(xx)
y_med = all_models["q 0.50"].predict(xx)
fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "black", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="Test observations")
plt.plot(xx, y_med, "tab:orange", linewidth=3, label="Predicted median")
plt.plot(xx, y_pred, "tab:green", linewidth=3, label="Predicted mean")
plt.fill_between(
xx.ravel(), y_lower, y_upper, alpha=0.4, label="Predicted 90% interval"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.show()
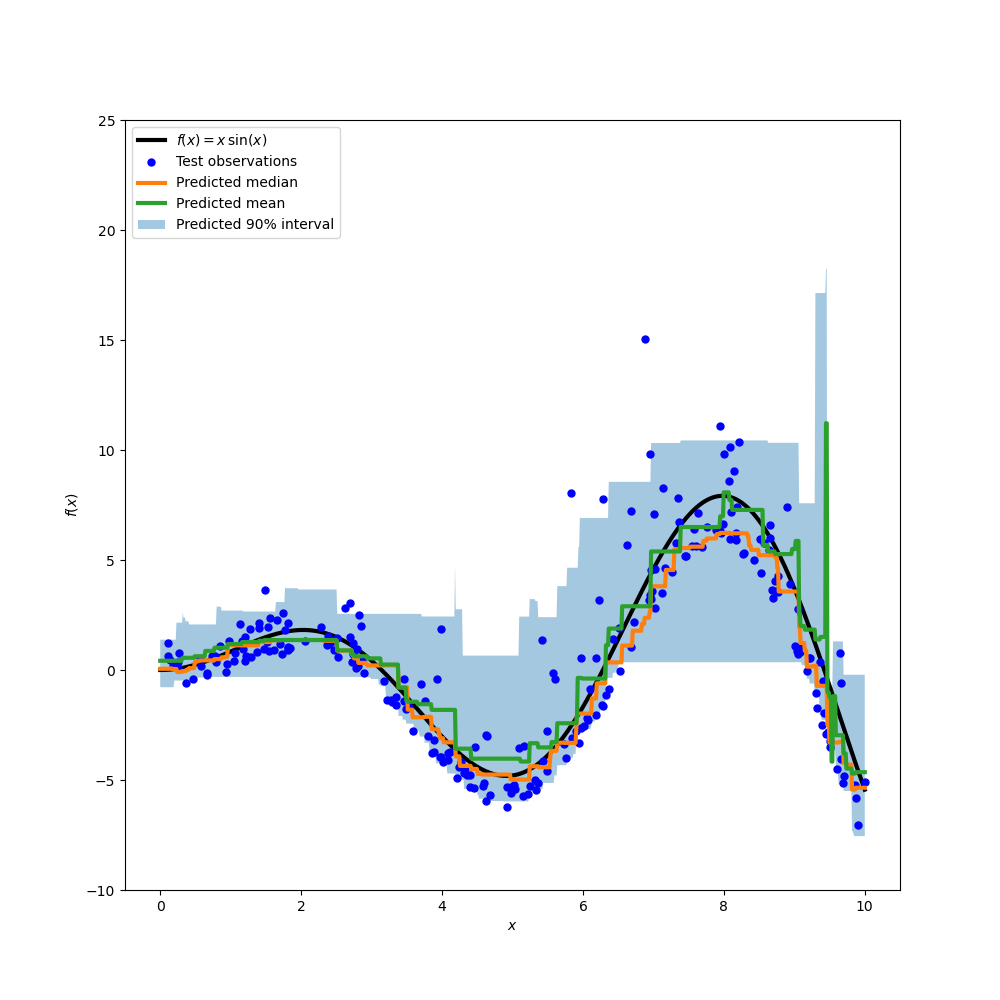
Сравнивая предсказанную медиану с предсказанным средним, мы отмечаем, что медиана в среднем ниже среднего, поскольку шум смещен в сторону высоких значений (большие выбросы). Оценка медианы также кажется более гладкой из-за её естественной устойчивости к выбросам.
Также обратите внимание, что индуктивное смещение деревьев градиентного бустинга, к сожалению, не позволяет нашему 0.05 квантилю полностью захватить синусоидальную форму сигнала, особенно вокруг x=8. Настройка гиперпараметров может уменьшить этот эффект, как показано в последней части этой тетради.
Анализ метрик ошибок#
Измерить модели с mean_squared_error и
mean_pinball_loss метрики на обучающем наборе данных.
import pandas as pd
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results = []
for name, gbr in sorted(all_models.items()):
metrics = {"model": name}
y_pred = gbr.predict(X_train)
for alpha in [0.05, 0.5, 0.95]:
metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(y_train, y_pred, alpha=alpha)
metrics["MSE"] = mean_squared_error(y_train, y_pred)
results.append(metrics)
pd.DataFrame(results).set_index("model").style.apply(highlight_min)
Один столбец показывает все модели, оцененные по одной и той же метрике. Минимальное значение в столбце должно достигаться, когда модель обучается и измеряется с той же метрикой. Это всегда должно быть так на обучающем наборе, если обучение сошлось.
Обратите внимание, что поскольку распределение целевой переменной асимметрично, ожидаемое условное среднее и условная медиана значительно отличаются, и поэтому нельзя использовать модель квадратичной ошибки для получения хорошей оценки условной медианы, и наоборот.
Если бы целевое распределение было симметричным и не имело выбросов (например, с гауссовским шумом), то медианный оценщик и оценщик наименьших квадратов дали бы схожие прогнозы.
Затем мы делаем то же самое на тестовом наборе.
results = []
for name, gbr in sorted(all_models.items()):
metrics = {"model": name}
y_pred = gbr.predict(X_test)
for alpha in [0.05, 0.5, 0.95]:
metrics["pbl=%1.2f" % alpha] = mean_pinball_loss(y_test, y_pred, alpha=alpha)
metrics["MSE"] = mean_squared_error(y_test, y_pred)
results.append(metrics)
pd.DataFrame(results).set_index("model").style.apply(highlight_min)
Ошибки выше, что означает, что модели слегка переобучили данные. Это все еще показывает, что лучшая тестовая метрика получается, когда модель обучается путем минимизации этой же метрики.
Обратите внимание, что оценка условной медианы конкурентоспособна с оценкой квадратичной ошибки с точки зрения MSE на тестовом наборе: это можно объяснить тем, что оценка квадратичной ошибки очень чувствительна к большим выбросам, которые могут вызвать значительное переобучение. Это видно на правой стороне предыдущего графика. Оценка условной медианы смещена (занижение для этого асимметричного шума), но также естественно устойчива к выбросам и меньше переобучается.
Калибровка доверительного интервала#
Мы также можем оценить способность двух экстремальных оценщиков квантилей создавать хорошо калиброванный условный 90%-доверительный интервал.
Для этого мы можем вычислить долю наблюдений, которые попадают между предсказаниями:
def coverage_fraction(y, y_low, y_high):
return np.mean(np.logical_and(y >= y_low, y <= y_high))
coverage_fraction(
y_train,
all_models["q 0.05"].predict(X_train),
all_models["q 0.95"].predict(X_train),
)
np.float64(0.9)
На обучающем наборе калибровка очень близка к ожидаемому значению покрытия для 90% доверительного интервала.
coverage_fraction(
y_test, all_models["q 0.05"].predict(X_test), all_models["q 0.95"].predict(X_test)
)
np.float64(0.868)
На тестовом наборе оцененный доверительный интервал немного слишком узок. Однако обратите внимание, что нам нужно будет обернуть эти метрики в цикл перекрестной проверки, чтобы оценить их изменчивость при повторной выборке данных.
Настройка гиперпараметров квантильных регрессоров#
На графике выше мы наблюдали, что регрессор 5-го процентиля, по-видимому, недообучается и не смог адаптироваться к синусоидальной форме сигнала.
Гиперпараметры модели были приблизительно настроены вручную для медианного регрессора, и нет причин, чтобы те же гиперпараметры были подходящими для регрессора 5-го процентиля.
Чтобы подтвердить эту гипотезу, мы настраиваем гиперпараметры нового регрессора 5-го процентиля, выбирая лучшие параметры модели с помощью кросс-валидации по функции потерь пинбола с alpha=0.05:
from pprint import pprint
from sklearn.experimental import enable_halving_search_cv # noqa: F401
from sklearn.metrics import make_scorer
from sklearn.model_selection import HalvingRandomSearchCV
param_grid = dict(
learning_rate=[0.05, 0.1, 0.2],
max_depth=[2, 5, 10],
min_samples_leaf=[1, 5, 10, 20],
min_samples_split=[5, 10, 20, 30, 50],
)
alpha = 0.05
neg_mean_pinball_loss_05p_scorer = make_scorer(
mean_pinball_loss,
alpha=alpha,
greater_is_better=False, # maximize the negative loss
)
gbr = GradientBoostingRegressor(loss="quantile", alpha=alpha, random_state=0)
search_05p = HalvingRandomSearchCV(
gbr,
param_grid,
resource="n_estimators",
max_resources=250,
min_resources=50,
scoring=neg_mean_pinball_loss_05p_scorer,
n_jobs=2,
random_state=0,
).fit(X_train, y_train)
pprint(search_05p.best_params_)
{'learning_rate': 0.2,
'max_depth': 2,
'min_samples_leaf': 20,
'min_samples_split': 10,
'n_estimators': 150}
Мы наблюдаем, что гиперпараметры, которые были настроены вручную для медианного регрессора, находятся в том же диапазоне, что и гиперпараметры, подходящие для регрессора 5-го процентиля.
Давайте теперь настроим гиперпараметры для регрессора 95-го процентиля. Нам
нужно переопределить scoring метрика, используемая для выбора лучшей модели, вместе с настройкой параметра alpha внутреннего градиентного бустингового оценщика:
from sklearn.base import clone
alpha = 0.95
neg_mean_pinball_loss_95p_scorer = make_scorer(
mean_pinball_loss,
alpha=alpha,
greater_is_better=False, # maximize the negative loss
)
search_95p = clone(search_05p).set_params(
estimator__alpha=alpha,
scoring=neg_mean_pinball_loss_95p_scorer,
)
search_95p.fit(X_train, y_train)
pprint(search_95p.best_params_)
{'learning_rate': 0.05,
'max_depth': 2,
'min_samples_leaf': 5,
'min_samples_split': 20,
'n_estimators': 150}
Результат показывает, что гиперпараметры для 95-го процентильного регрессора, определенные процедурой поиска, примерно в том же диапазоне, что и вручную настроенные гиперпараметры для медианного регрессора и гиперпараметры, определенные процедурой поиска для 5-го процентильного регрессора. Однако поиск гиперпараметров привел к улучшенному 90% доверительному интервалу, который состоит из предсказаний этих двух настроенных квантильных регрессоров. Обратите внимание, что предсказание верхнего 95-го процентиля имеет гораздо более грубую форму, чем предсказание нижнего 5-го процентиля, из-за выбросов:
y_lower = search_05p.predict(xx)
y_upper = search_95p.predict(xx)
fig = plt.figure(figsize=(10, 10))
plt.plot(xx, f(xx), "black", linewidth=3, label=r"$f(x) = x\,\sin(x)$")
plt.plot(X_test, y_test, "b.", markersize=10, label="Test observations")
plt.fill_between(
xx.ravel(), y_lower, y_upper, alpha=0.4, label="Predicted 90% interval"
)
plt.xlabel("$x$")
plt.ylabel("$f(x)$")
plt.ylim(-10, 25)
plt.legend(loc="upper left")
plt.title("Prediction with tuned hyper-parameters")
plt.show()
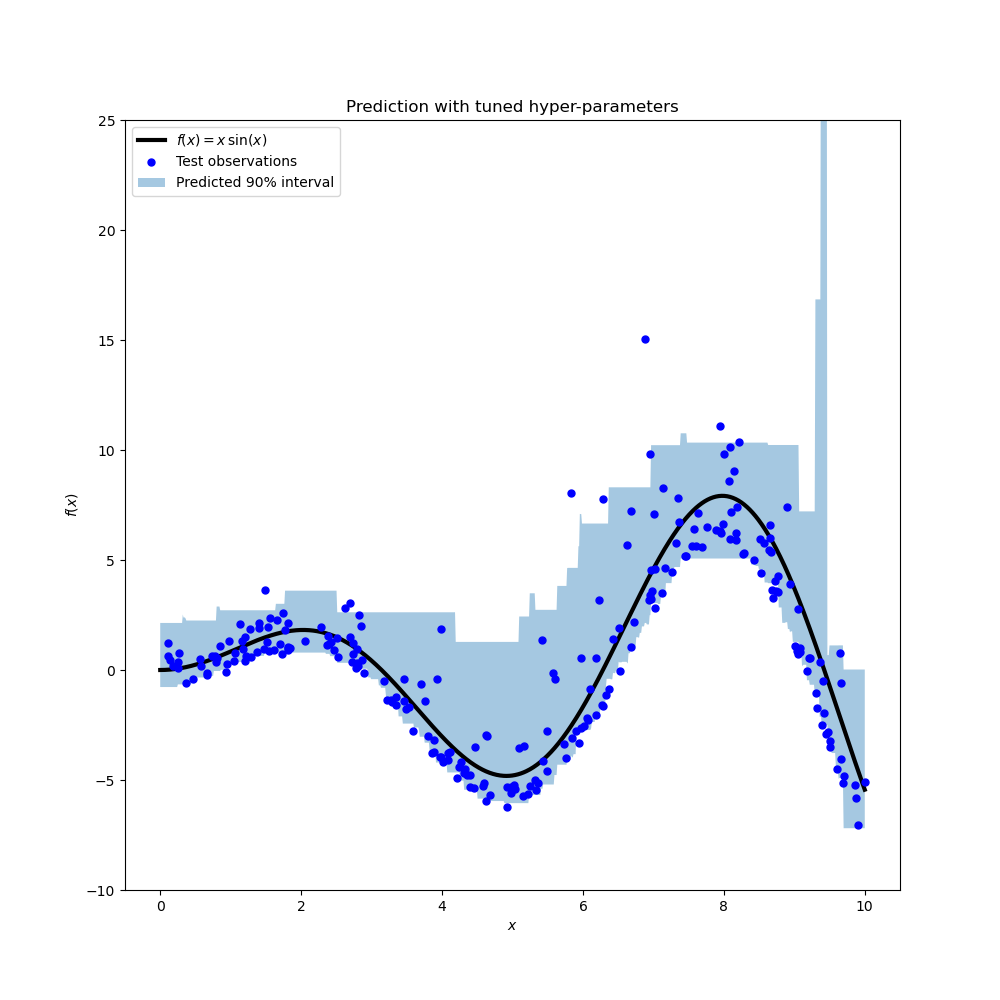
График выглядит качественно лучше, чем для ненастроенных моделей, особенно по форме нижнего квантиля.
Теперь мы количественно оцениваем совместную калибровку пары оценщиков:
coverage_fraction(y_train, search_05p.predict(X_train), search_95p.predict(X_train))
np.float64(0.9026666666666666)
coverage_fraction(y_test, search_05p.predict(X_test), search_95p.predict(X_test))
np.float64(0.796)
Калибровка настроенной пары, к сожалению, не лучше на тестовом наборе: ширина оцененного доверительного интервала все еще слишком узкая.
Опять же, нам нужно обернуть это исследование в цикл перекрёстной проверки, чтобы лучше оценить изменчивость этих оценок.
Общее время выполнения скрипта: (0 минут 10.855 секунд)
Связанные примеры
Лаггированные признаки для прогнозирования временных рядов
Регрессия гауссовских процессов: базовый вводный пример