Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Один оценщик против бэггинга: декомпозиция смещения-дисперсии#

Этот пример иллюстрирует и сравнивает разложение смещения-дисперсии ожидаемой среднеквадратичной ошибки одного оценщика против ансамбля бэггинга.

В регрессии ожидаемая среднеквадратичная ошибка оценщика может быть разложена на составляющие смещения, дисперсии и шума. В среднем по наборам данных регрессионной задачи, член смещения измеряет среднюю величину, на которую прогнозы оценщика отличаются от прогнозов наилучшего возможного оценщика для задачи (т.е. байесовской модели). Член дисперсии измеряет изменчивость прогнозов оценщика при обучении на различных случайных экземплярах одной и той же задачи. Каждый экземпляр задачи обозначается «LS», для «Обучающей Выборки» в дальнейшем. Наконец, шум измеряет несократимую часть ошибки, обусловленную изменчивостью данных.

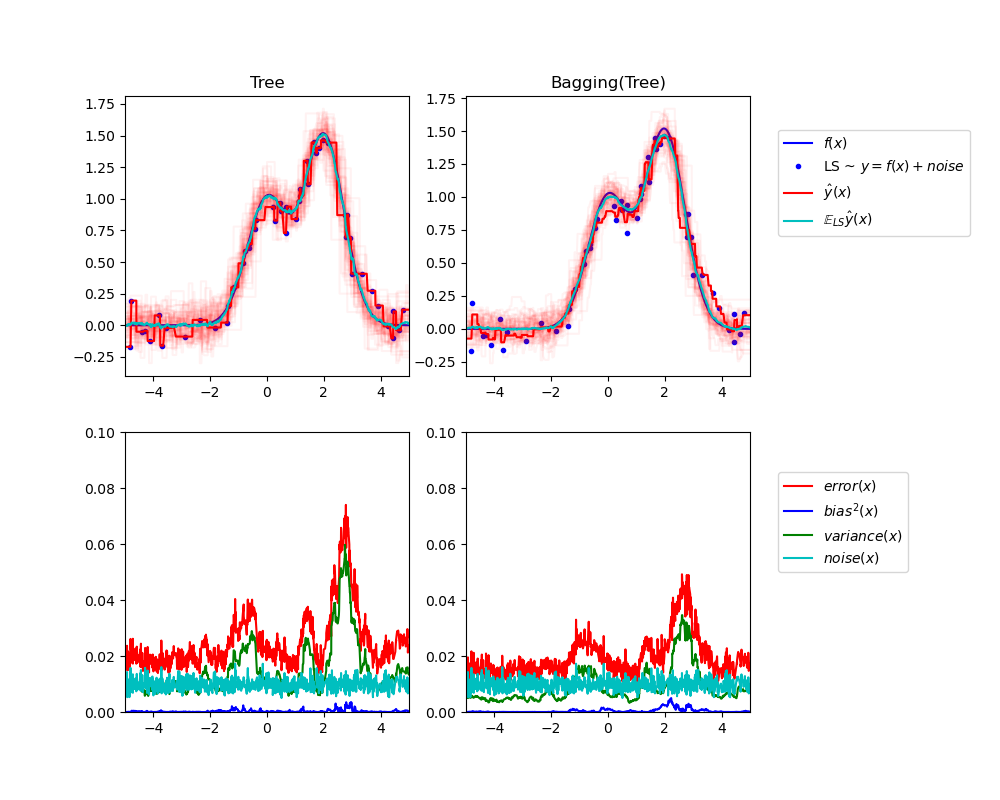
Верхний левый рисунок иллюстрирует предсказания (темно-красным) одного дерева решений, обученного на случайном наборе данных LS (синие точки) для игрушечной 1D задачи регрессии. Он также показывает предсказания (светло-красным) других отдельных деревьев решений, обученных на других (и различных) случайно выбранных экземплярах LS задачи. Интуитивно, член дисперсии здесь соответствует ширине пучка предсказаний (светло-красным) отдельных оценщиков. Чем больше дисперсия, тем более чувствительны предсказания к x к небольшим изменениям в обучающем наборе. Смещение соответствует разнице между средним предсказанием оценщика (в голубом) и наилучшей возможной моделью (в тёмно-синем). На этой задаче мы можем наблюдать, что смещение довольно низкое (обе кривые, голубая и синяя, близки друг к другу), в то время как дисперсия велика (красный луч довольно широк).

Нижний левый график показывает поточечное разложение ожидаемой средней квадратичной ошибки одного дерева решений. Он подтверждает, что член смещения (синий) низкий, в то время как дисперсия велика (зеленый). Он также иллюстрирует шумовую часть ошибки, которая, как и ожидалось, остается постоянной и около 0.01.

Правые графики соответствуют тем же построениям, но с использованием ансамбля бэггинга на деревьях решений. На обоих графиках можно наблюдать, что член смещения больше, чем в предыдущем случае. На верхнем правом графике разница между средним предсказанием (голубым) и наилучшей возможной моделью больше (например, обратите внимание на смещение вокруг x=2). На нижнем правом графике кривая смещения также немного выше, чем на нижнем левом графике. С точки зрения дисперсии, однако, разброс предсказаний уже, что предполагает, что дисперсия ниже. Действительно, как подтверждает нижний правый график, член дисперсии (зеленый) ниже, чем для отдельных деревьев решений. В целом, декомпозиция смещения-дисперсии поэтому больше не одинакова. Компромисс лучше для бэггинга: усреднение нескольких деревьев решений, обученных на бутстрап-копиях набора данных, немного увеличивает член смещения, но позволяет больше сократить дисперсию, что приводит к меньшей общей среднеквадратичной ошибке (сравните красные кривые на нижних графиках). Вывод скрипта также подтверждает эту интуицию. Общая ошибка ансамбля бэггинга ниже общей ошибки одного дерева решений, и эта разница действительно в основном обусловлена сниженной дисперсией.

Для получения дополнительных сведений о разложении смещения-дисперсии см. раздел 7.3 [1].

Ссылки#

Tree: 0.0255 (error) = 0.0003 (bias^2)  + 0.0152 (var) + 0.0098 (noise)
Bagging(Tree): 0.0196 (error) = 0.0004 (bias^2)  + 0.0092 (var) + 0.0098 (noise)

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.ensemble import BaggingRegressor
from sklearn.tree import DecisionTreeRegressor

# Settings
n_repeat = 50  # Number of iterations for computing expectations
n_train = 50  # Size of the training set
n_test = 1000  # Size of the test set
noise = 0.1  # Standard deviation of the noise
np.random.seed(0)

# Change this for exploring the bias-variance decomposition of other
# estimators. This should work well for estimators with high variance (e.g.,
# decision trees or KNN), but poorly for estimators with low variance (e.g.,
# linear models).
estimators = [
    ("Tree", DecisionTreeRegressor()),
    ("Bagging(Tree)", BaggingRegressor(DecisionTreeRegressor())),
]

n_estimators = len(estimators)


# Generate data
def f(x):
    x = x.ravel()

    return np.exp(-(x**2)) + 1.5 * np.exp(-((x - 2) ** 2))


def generate(n_samples, noise, n_repeat=1):
    X = np.random.rand(n_samples) * 10 - 5
    X = np.sort(X)

    if n_repeat == 1:
        y = f(X) + np.random.normal(0.0, noise, n_samples)
    else:
        y = np.zeros((n_samples, n_repeat))

        for i in range(n_repeat):
            y[:, i] = f(X) + np.random.normal(0.0, noise, n_samples)

    X = X.reshape((n_samples, 1))

    return X, y


X_train = []
y_train = []

for i in range(n_repeat):
    X, y = generate(n_samples=n_train, noise=noise)
    X_train.append(X)
    y_train.append(y)

X_test, y_test = generate(n_samples=n_test, noise=noise, n_repeat=n_repeat)

plt.figure(figsize=(10, 8))

# Loop over estimators to compare
for n, (name, estimator) in enumerate(estimators):
    # Compute predictions
    y_predict = np.zeros((n_test, n_repeat))

    for i in range(n_repeat):
        estimator.fit(X_train[i], y_train[i])
        y_predict[:, i] = estimator.predict(X_test)

    # Bias^2 + Variance + Noise decomposition of the mean squared error
    y_error = np.zeros(n_test)

    for i in range(n_repeat):
        for j in range(n_repeat):
            y_error += (y_test[:, j] - y_predict[:, i]) ** 2

    y_error /= n_repeat * n_repeat

    y_noise = np.var(y_test, axis=1)
    y_bias = (f(X_test) - np.mean(y_predict, axis=1)) ** 2
    y_var = np.var(y_predict, axis=1)

    print(
        "{0}: {1:.4f} (error) = {2:.4f} (bias^2) "
        " + {3:.4f} (var) + {4:.4f} (noise)".format(
            name, np.mean(y_error), np.mean(y_bias), np.mean(y_var), np.mean(y_noise)
        )
    )

    # Plot figures
    plt.subplot(2, n_estimators, n + 1)
    plt.plot(X_test, f(X_test), "b", label="$f(x)$")
    plt.plot(X_train[0], y_train[0], ".b", label="LS ~ $y = f(x)+noise$")

    for i in range(n_repeat):
        if i == 0:
            plt.plot(X_test, y_predict[:, i], "r", label=r"$\^y(x)$")
        else:
            plt.plot(X_test, y_predict[:, i], "r", alpha=0.05)

    plt.plot(X_test, np.mean(y_predict, axis=1), "c", label=r"$\mathbb{E}_{LS} \^y(x)$")

    plt.xlim([-5, 5])
    plt.title(name)

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

    plt.subplot(2, n_estimators, n_estimators + n + 1)
    plt.plot(X_test, y_error, "r", label="$error(x)$")
    plt.plot(X_test, y_bias, "b", label="$bias^2(x)$")
    plt.plot(X_test, y_var, "g", label="$variance(x)$")
    plt.plot(X_test, y_noise, "c", label="$noise(x)$")

    plt.xlim([-5, 5])
    plt.ylim([0, 0.1])

    if n == n_estimators - 1:
        plt.legend(loc=(1.1, 0.5))

plt.subplots_adjust(right=0.75)
plt.show()