Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Двухклассовый AdaBoost#
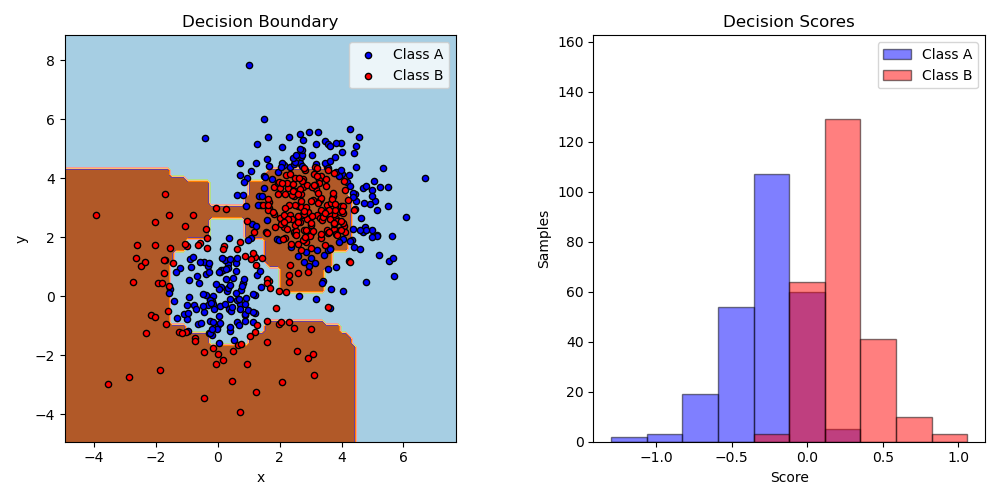
Этот пример обучает решающий пень с AdaBoost на нелинейно разделимом наборе данных классификации, состоящем из двух кластеров «Гауссовых квантилей» (см. sklearn.datasets.make_gaussian_quantiles) и отображает границу решения и оценки решения. Распределения оценок решения показаны отдельно для выборок класса A и B. Предсказанная метка класса для каждой выборки определяется знаком оценки решения. Выборки с оценками решения больше нуля классифицируются как B, в противном случае как A. Величина оценки решения определяет степень сходства с предсказанной меткой класса. Кроме того, можно создать новый набор данных с желаемой чистотой класса B, например, выбирая только выборки с оценкой решения выше некоторого значения.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_gaussian_quantiles
from sklearn.ensemble import AdaBoostClassifier
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.tree import DecisionTreeClassifier
# Construct dataset
X1, y1 = make_gaussian_quantiles(
cov=2.0, n_samples=200, n_features=2, n_classes=2, random_state=1
)
X2, y2 = make_gaussian_quantiles(
mean=(3, 3), cov=1.5, n_samples=300, n_features=2, n_classes=2, random_state=1
)
X = np.concatenate((X1, X2))
y = np.concatenate((y1, -y2 + 1))
# Create and fit an AdaBoosted decision tree
bdt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1), n_estimators=200)
bdt.fit(X, y)
plot_colors = "br"
plot_step = 0.02
class_names = "AB"
plt.figure(figsize=(10, 5))
# Plot the decision boundaries
ax = plt.subplot(121)
disp = DecisionBoundaryDisplay.from_estimator(
bdt,
X,
cmap=plt.cm.Paired,
response_method="predict",
ax=ax,
xlabel="x",
ylabel="y",
)
x_min, x_max = disp.xx0.min(), disp.xx0.max()
y_min, y_max = disp.xx1.min(), disp.xx1.max()
plt.axis("tight")
# Plot the training points
for i, n, c in zip(range(2), class_names, plot_colors):
idx = (y == i).nonzero()
plt.scatter(
X[idx, 0],
X[idx, 1],
c=c,
s=20,
edgecolor="k",
label="Class %s" % n,
)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.legend(loc="upper right")
plt.title("Decision Boundary")
# Plot the two-class decision scores
twoclass_output = bdt.decision_function(X)
plot_range = (twoclass_output.min(), twoclass_output.max())
plt.subplot(122)
for i, n, c in zip(range(2), class_names, plot_colors):
plt.hist(
twoclass_output[y == i],
bins=10,
range=plot_range,
facecolor=c,
label="Class %s" % n,
alpha=0.5,
edgecolor="k",
)
x1, x2, y1, y2 = plt.axis()
plt.axis((x1, x2, y1, y2 * 1.2))
plt.legend(loc="upper right")
plt.ylabel("Samples")
plt.xlabel("Score")
plt.title("Decision Scores")
plt.tight_layout()
plt.subplots_adjust(wspace=0.35)
plt.show()
Общее время выполнения скрипта: (0 минут 0.694 секунды)
Связанные примеры

SGD: Гиперплоскость максимального разделяющего запаса

Построить поверхности решений ансамблей деревьев на наборе данных ирисов
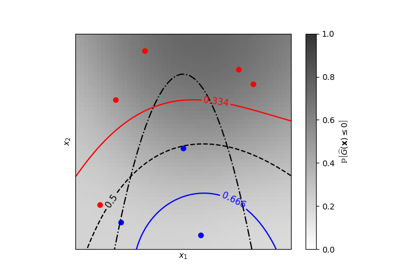
Изолинии равной вероятности для классификации гауссовских процессов (GPC)
