Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Построить график вероятности классификации#
Этот пример иллюстрирует использование
sklearn.inspection.DecisionBoundaryDisplay для построения предсказанных вероятностей классов различных классификаторов в двумерном пространстве признаков, в основном в дидактических целях.
Многослойный перцептрон чувствителен к масштабированию признаков, поэтому настоятельно рекомендуется масштабировать ваши данные. Например, масштабируйте каждый атрибут входного вектора X до [0, 1] или [-1, +1] или стандартизируйте его до среднего 0 и дисперсии 1. Обратите внимание, что вы должны применить
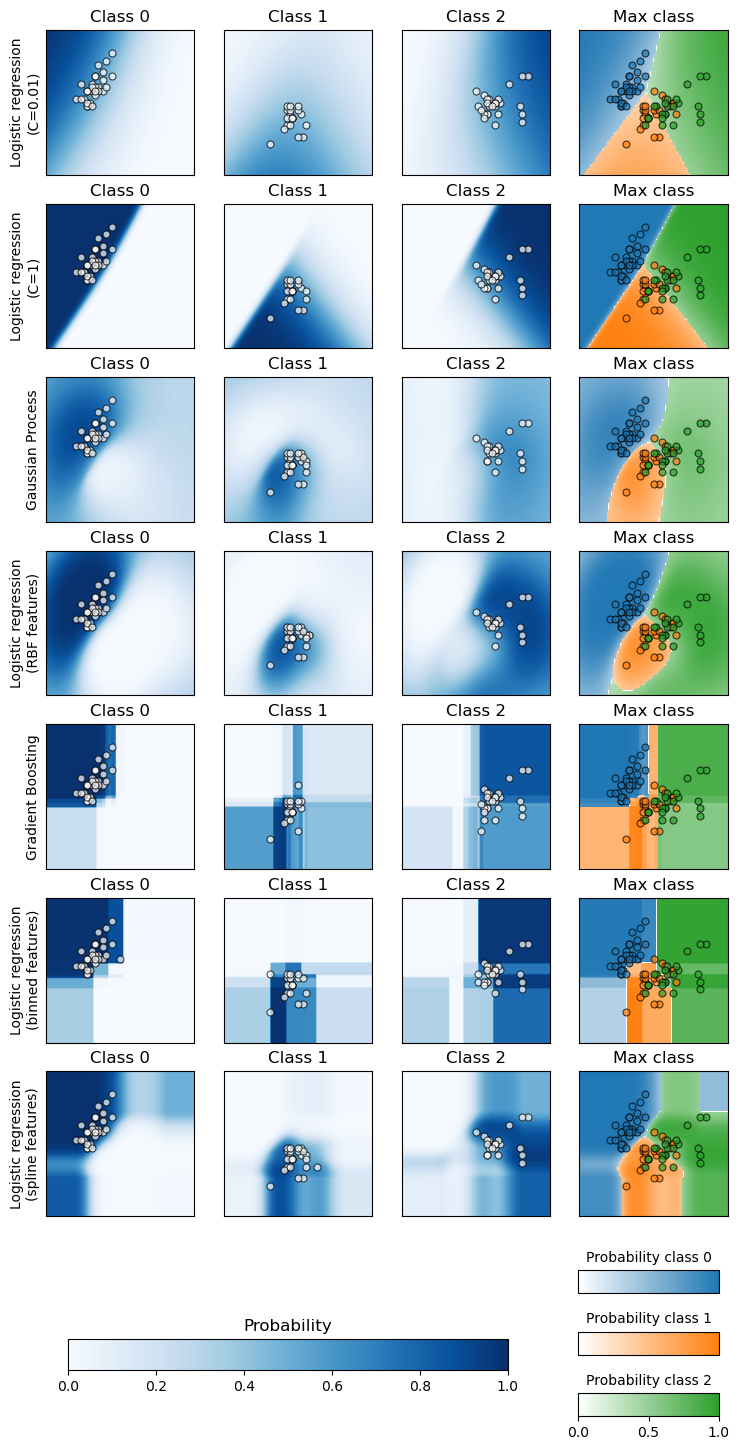
В последнем столбце все три класса представлены на каждом графике; класс с наивысшей предсказанной вероятностью в каждой точке отображается. Круглые маркеры показывают тестовые данные и окрашены в соответствии с их истинной меткой.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from matplotlib import cm
from sklearn import datasets
from sklearn.ensemble import HistGradientBoostingClassifier
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn.inspection import DecisionBoundaryDisplay
from sklearn.kernel_approximation import Nystroem
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, log_loss, roc_auc_score
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import (
KBinsDiscretizer,
PolynomialFeatures,
SplineTransformer,
)
Данные: 2D проекция набора данных ирисов#
iris = datasets.load_iris()
X = iris.data[:, 0:2] # we only take the first two features for visualization
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.5, random_state=42
)
Вероятностные классификаторы#
Мы построим границы решений нескольких классификаторов, которые имеют
predict_proba метод. Это позволит нам визуализировать неопределенность классификатора в регионах, где он не уверен в своем прогнозе.
classifiers = {
"Logistic regression\n(C=0.01)": LogisticRegression(C=0.1),
"Logistic regression\n(C=1)": LogisticRegression(C=100),
"Gaussian Process": GaussianProcessClassifier(kernel=1.0 * RBF([1.0, 1.0])),
"Logistic regression\n(RBF features)": make_pipeline(
Nystroem(kernel="rbf", gamma=5e-1, n_components=50, random_state=1),
LogisticRegression(C=10),
),
"Gradient Boosting": HistGradientBoostingClassifier(),
"Logistic regression\n(binned features)": make_pipeline(
KBinsDiscretizer(n_bins=5, quantile_method="averaged_inverted_cdf"),
PolynomialFeatures(interaction_only=True),
LogisticRegression(C=10),
),
"Logistic regression\n(spline features)": make_pipeline(
SplineTransformer(n_knots=5),
PolynomialFeatures(interaction_only=True),
LogisticRegression(C=10),
),
}
Построение границ решений#
Для каждого классификатора мы отображаем вероятности по классам в первых трех столбцах и вероятности наиболее вероятного класса в последнем столбце.
n_classifiers = len(classifiers)
scatter_kwargs = {
"s": 25,
"marker": "o",
"linewidths": 0.8,
"edgecolor": "k",
"alpha": 0.7,
}
y_unique = np.unique(y)
# Ensure legend not cut off
mpl.rcParams["savefig.bbox"] = "tight"
fig, axes = plt.subplots(
nrows=n_classifiers,
ncols=len(iris.target_names) + 1,
figsize=(4 * 2.2, n_classifiers * 2.2),
)
evaluation_results = []
levels = 100
for classifier_idx, (name, classifier) in enumerate(classifiers.items()):
y_pred = classifier.fit(X_train, y_train).predict(X_test)
y_pred_proba = classifier.predict_proba(X_test)
accuracy_test = accuracy_score(y_test, y_pred)
roc_auc_test = roc_auc_score(y_test, y_pred_proba, multi_class="ovr")
log_loss_test = log_loss(y_test, y_pred_proba)
evaluation_results.append(
{
"name": name.replace("\n", " "),
"accuracy": accuracy_test,
"roc_auc": roc_auc_test,
"log_loss": log_loss_test,
}
)
for label in y_unique:
# plot the probability estimate provided by the classifier
disp = DecisionBoundaryDisplay.from_estimator(
classifier,
X_train,
response_method="predict_proba",
class_of_interest=label,
ax=axes[classifier_idx, label],
vmin=0,
vmax=1,
cmap="Blues",
levels=levels,
)
axes[classifier_idx, label].set_title(f"Class {label}")
# plot data predicted to belong to given class
mask_y_pred = y_pred == label
axes[classifier_idx, label].scatter(
X_test[mask_y_pred, 0], X_test[mask_y_pred, 1], c="w", **scatter_kwargs
)
axes[classifier_idx, label].set(xticks=(), yticks=())
# add column that shows all classes by plotting class with max 'predict_proba'
max_class_disp = DecisionBoundaryDisplay.from_estimator(
classifier,
X_train,
response_method="predict_proba",
class_of_interest=None,
ax=axes[classifier_idx, len(y_unique)],
vmin=0,
vmax=1,
levels=levels,
)
for label in y_unique:
mask_label = y_test == label
axes[classifier_idx, 3].scatter(
X_test[mask_label, 0],
X_test[mask_label, 1],
c=max_class_disp.multiclass_colors_[[label], :],
**scatter_kwargs,
)
axes[classifier_idx, 3].set(xticks=(), yticks=())
axes[classifier_idx, 3].set_title("Max class")
axes[classifier_idx, 0].set_ylabel(name)
# colorbar for single class plots
ax_single = fig.add_axes([0.15, 0.01, 0.5, 0.02])
plt.title("Probability")
_ = plt.colorbar(
cm.ScalarMappable(norm=None, cmap=disp.surface_.cmap),
cax=ax_single,
orientation="horizontal",
)
# colorbars for max probability class column
max_class_cmaps = [s.cmap for s in max_class_disp.surface_]
for label in y_unique:
ax_max = fig.add_axes([0.73, (0.06 - (label * 0.04)), 0.16, 0.015])
plt.title(f"Probability class {label}", fontsize=10)
_ = plt.colorbar(
cm.ScalarMappable(norm=None, cmap=max_class_cmaps[label]),
cax=ax_max,
orientation="horizontal",
)
if label in (0, 1):
ax_max.set(xticks=(), yticks=())
Количественная оценка#
pd.DataFrame(evaluation_results).round(2)
Анализ#
Две модели логистической регрессии, обученные на исходных признаках, демонстрируют
линейные границы решений, как и ожидалось. Для этой конкретной задачи это
не кажется вредным, так как обе модели конкурентоспособны с
нелинейными моделями при количественной оценке на тестовом наборе. Мы можем
наблюдать, что количество регуляризации влияет на уверенность модели:
более светлые цвета для сильно регуляризованной модели с меньшим значением C. Регуляризация также влияет на ориентацию границы решений, приводя к несколько другому ROC AUC.
Лог-потери, с другой стороны, оценивают как резкость, так и калибровку и, как следствие, сильно предпочитают слабо регуляризованную модель логистической регрессии, вероятно, потому что сильно регуляризованная модель недостаточно уверена. Это можно подтвердить, посмотрев на кривую калибровки с помощью
sklearn.calibration.CalibrationDisplay.
Логистическая регрессия с RBF-признаками имеет "каплевидную" границу решения, которая нелинейна в исходном пространстве признаков и весьма похожа на границу решения классификатора на основе гауссовского процесса, настроенного на использование RBF-ядра.
Логистическая регрессия, обученная на бинированных признаках с взаимодействиями, имеет границу решения, которая нелинейна в исходном пространстве признаков и довольно похожа на границу решения градиентного бустинга: обе модели предпочитают выравнивание по осям при экстраполяции на невидимые области пространства признаков.
Логистическая регрессионная модель, обученная на сплайн-признаках с взаимодействиями, имеет схожее поведение экстраполяции, выровненное по осям, но более гладкую границу решений в плотной области пространства признаков, чем две предыдущие модели.
В заключение интересно отметить, что проектирование признаков для моделей логистической регрессии может использоваться для имитации некоторых индуктивных смещений различных нелинейных моделей. Однако для этого конкретного набора данных использования сырых признаков достаточно для обучения конкурентоспособной модели. Это не обязательно будет так для других наборов данных.
Общее время выполнения скрипта: (0 минут 2.482 секунды)
Связанные примеры
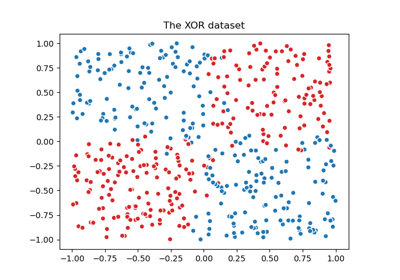
Визуализация вероятностных предсказаний VotingClassifier

Признаки ограниченной машины Больцмана для классификации цифр
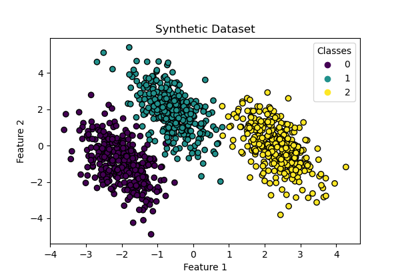
Границы решений мультиномиальной и логистической регрессии One-vs-Rest