Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Метод наименьших квадратов и гребневая регрессия#
Метод наименьших квадратов: Мы иллюстрируем, как использовать модель обычного метода наименьших квадратов (OLS),
LinearRegression, на одном признаке набора данных о диабете. Мы обучаем на подмножестве данных, оцениваем на тестовом наборе и визуализируем предсказания.Обычный метод наименьших квадратов и дисперсия регрессии Риджа: Затем мы показываем, как OLS может иметь высокую дисперсию, когда данные разреженные или зашумленные, путем многократной подгонки на очень маленькой синтетической выборке. Регрессия Риджа,
Ridge, уменьшает эту дисперсию путём штрафования (сжатия) коэффициентов, что приводит к более устойчивым предсказаниям.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Загрузка и подготовка данных#
Загрузите набор данных по диабету. Для простоты мы оставляем только один признак в данных. Затем мы разделяем данные и целевую переменную на обучающую и тестовую выборки.
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
X, y = load_diabetes(return_X_y=True)
X = X[:, [2]] # Use only one feature
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=20, shuffle=False)
Модель линейной регрессии#
Мы создаем модель линейной регрессии и обучаем ее на тренировочных данных. Обратите внимание, что по
умолчанию к модели добавляется свободный член. Мы можем управлять этим поведением, устанавливая fit_intercept параметр.
from sklearn.linear_model import LinearRegression
regressor = LinearRegression().fit(X_train, y_train)
Оценка модели#
Мы оцениваем производительность модели на тестовом наборе данных, используя среднеквадратичную ошибку и коэффициент детерминации.
from sklearn.metrics import mean_squared_error, r2_score
y_pred = regressor.predict(X_test)
print(f"Mean squared error: {mean_squared_error(y_test, y_pred):.2f}")
print(f"Coefficient of determination: {r2_score(y_test, y_pred):.2f}")
Mean squared error: 2548.07
Coefficient of determination: 0.47
Построение графиков результатов#
Наконец, мы визуализируем результаты на обучающих и тестовых данных.
import matplotlib.pyplot as plt
fig, ax = plt.subplots(ncols=2, figsize=(10, 5), sharex=True, sharey=True)
ax[0].scatter(X_train, y_train, label="Train data points")
ax[0].plot(
X_train,
regressor.predict(X_train),
linewidth=3,
color="tab:orange",
label="Model predictions",
)
ax[0].set(xlabel="Feature", ylabel="Target", title="Train set")
ax[0].legend()
ax[1].scatter(X_test, y_test, label="Test data points")
ax[1].plot(X_test, y_pred, linewidth=3, color="tab:orange", label="Model predictions")
ax[1].set(xlabel="Feature", ylabel="Target", title="Test set")
ax[1].legend()
fig.suptitle("Linear Regression")
plt.show()
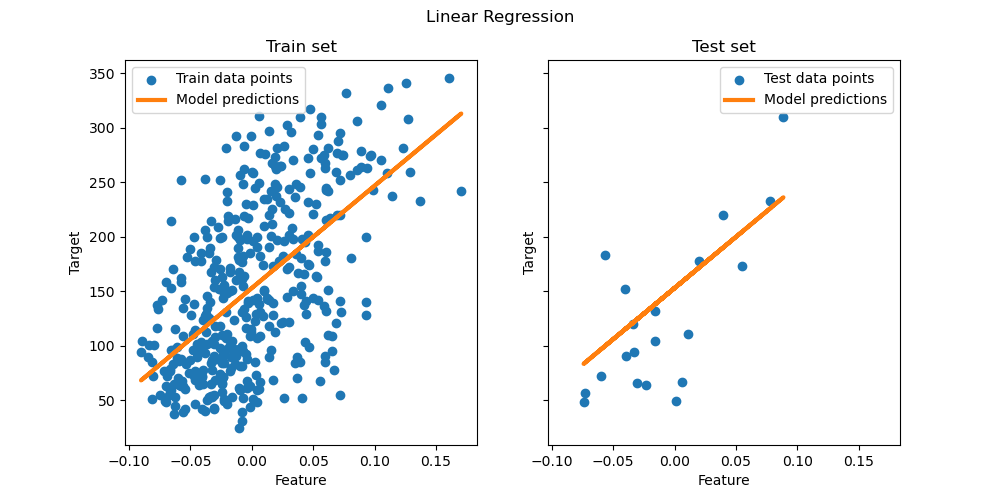
OLS на этом подмножестве с одним признаком изучает линейную функцию, которая минимизирует среднюю квадратичную ошибку на обучающих данных. Мы можем увидеть, насколько хорошо (или плохо) она обобщается, посмотрев на оценку R^2 и среднюю квадратичную ошибку на тестовом наборе. В более высоких измерениях чистый OLS часто переобучается, особенно если данные зашумлены. Методы регуляризации (такие как Ridge или Lasso) могут помочь уменьшить это.
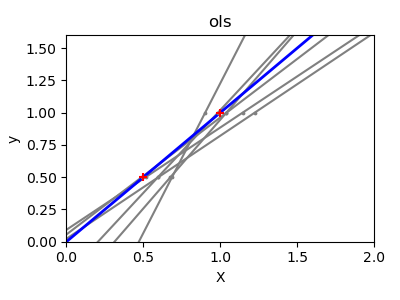
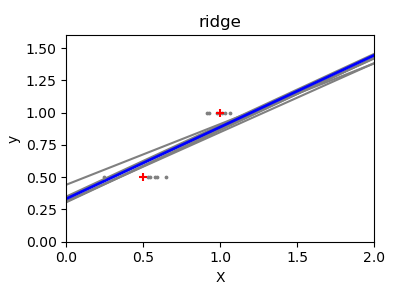
Обычный метод наименьших квадратов и дисперсия регрессии Риджа#
Далее мы более наглядно иллюстрируем проблему высокой дисперсии, используя небольшой синтетический набор данных. Мы берем только две точки данных, затем многократно добавляем к ним небольшой гауссовский шум и заново обучаем как OLS, так и Ridge. Мы строим каждую новую линию, чтобы увидеть, насколько сильно может колебаться OLS, тогда как Ridge остается более стабильным благодаря своему штрафному члену.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
X_train = np.c_[0.5, 1].T
y_train = [0.5, 1]
X_test = np.c_[0, 2].T
np.random.seed(0)
classifiers = dict(
ols=linear_model.LinearRegression(), ridge=linear_model.Ridge(alpha=0.1)
)
for name, clf in classifiers.items():
fig, ax = plt.subplots(figsize=(4, 3))
for _ in range(6):
this_X = 0.1 * np.random.normal(size=(2, 1)) + X_train
clf.fit(this_X, y_train)
ax.plot(X_test, clf.predict(X_test), color="gray")
ax.scatter(this_X, y_train, s=3, c="gray", marker="o", zorder=10)
clf.fit(X_train, y_train)
ax.plot(X_test, clf.predict(X_test), linewidth=2, color="blue")
ax.scatter(X_train, y_train, s=30, c="red", marker="+", zorder=10)
ax.set_title(name)
ax.set_xlim(0, 2)
ax.set_ylim((0, 1.6))
ax.set_xlabel("X")
ax.set_ylabel("y")
fig.tight_layout()
plt.show()
Заключение#
В первом примере мы применили OLS к реальному набору данных, показав, как простая линейная модель может соответствовать данным, минимизируя квадратичную ошибку на обучающей выборке.
Во втором примере линии OLS сильно менялись каждый раз при добавлении шума, что отражает высокую дисперсию при разреженных или зашумленных данных. В отличие от этого, Ridge регрессия вводит регуляризационный член, который сжимает коэффициенты, стабилизируя предсказания.
Такие методы, как Ridge или
Lasso (который применяет штраф L1) являются распространёнными способами улучшения обобщения и уменьшения переобучения. Хорошо настроенные Ridge или Lasso часто превосходят чистый OLS, когда признаки коррелированы, данные зашумлены или размер выборки мал.
Общее время выполнения скрипта: (0 минут 0.369 секунд)
Связанные примеры
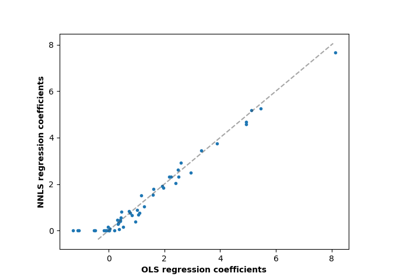
Метод наименьших квадратов с неотрицательными ограничениями
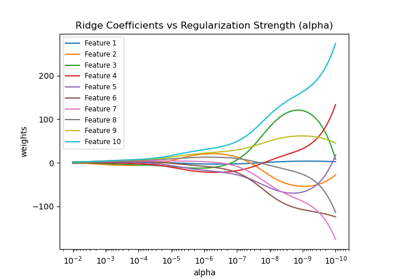
Построение коэффициентов Ridge как функции регуляризации
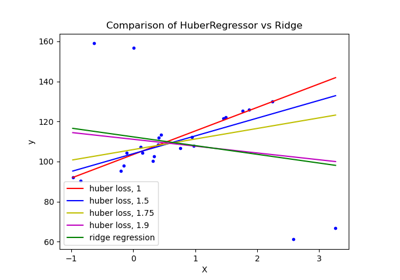
HuberRegressor против Ridge на наборе данных с сильными выбросами
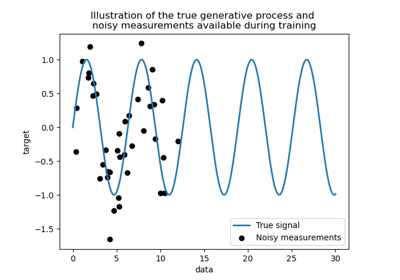
Сравнение ядерной гребневой регрессии и регрессии по методу Гауссовских процессов