Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Выбор модели Lasso с помощью информационных критериев#
Этот пример воспроизводит пример из рис. 2 [ZHT2007]. A
LassoLarsIC оценщик обучается на наборе данных по диабету, и для выбора лучшей модели используются критерии AIC и BIC.
Примечание
Важно отметить, что оптимизация для нахождения alpha с
LassoLarsIC основывается на критериях AIC или BIC, которые вычисляются внутри выборки, то есть непосредственно на обучающем наборе. Этот подход отличается от процедуры перекрестной проверки. Для сравнения двух подходов вы можете обратиться к следующему примеру:
Выбор модели Lasso: AIC-BIC / перекрёстная проверка.
Ссылки
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Мы будем использовать набор данных по диабету.
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
n_samples = X.shape[0]
X.head()
Scikit-learn предоставляет оценщик под названием
LassoLarsIC которая использует либо информационный критерий Акаике (AIC), либо байесовский информационный критерий (BIC) для выбора наилучшей модели. Перед обучением этой модели мы масштабируем набор данных.
Далее мы обучим две модели, чтобы сравнить значения, сообщаемые AIC и BIC.
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
Чтобы соответствовать определению в [ZHT2007], нам нужно перемасштабировать AIC и BIC. Действительно, Zou et al. игнорируют некоторые постоянные члены по сравнению с исходным определением AIC, выведенным из максимального логарифма правдоподобия линейной модели. Вы можете обратиться к раздел с математическими деталями для руководства пользователя.
import numpy as np
aic_criterion = zou_et_al_criterion_rescaling(
lasso_lars_ic[-1].criterion_,
n_samples,
lasso_lars_ic[-1].noise_variance_,
)
index_alpha_path_aic = np.flatnonzero(
lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
bic_criterion = zou_et_al_criterion_rescaling(
lasso_lars_ic[-1].criterion_,
n_samples,
lasso_lars_ic[-1].noise_variance_,
)
index_alpha_path_bic = np.flatnonzero(
lasso_lars_ic[-1].alphas_ == lasso_lars_ic[-1].alpha_
)[0]
Теперь, когда мы собрали AIC и BIC, мы также можем проверить, что минимумы обоих критериев достигаются при одном и том же alpha. Затем мы можем упростить следующий график.
index_alpha_path_aic == index_alpha_path_bic
np.True_
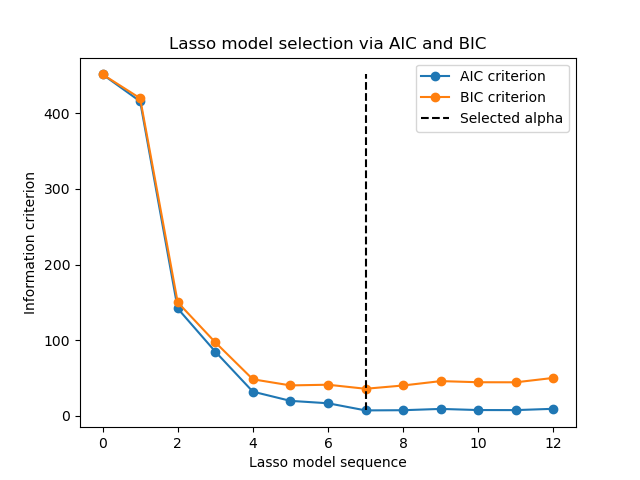
Наконец, мы можем построить критерии AIC и BIC и последующий выбранный параметр регуляризации.
import matplotlib.pyplot as plt
plt.plot(aic_criterion, color="tab:blue", marker="o", label="AIC criterion")
plt.plot(bic_criterion, color="tab:orange", marker="o", label="BIC criterion")
plt.vlines(
index_alpha_path_bic,
aic_criterion.min(),
aic_criterion.max(),
color="black",
linestyle="--",
label="Selected alpha",
)
plt.legend()
plt.ylabel("Information criterion")
plt.xlabel("Lasso model sequence")
_ = plt.title("Lasso model selection via AIC and BIC")
Общее время выполнения скрипта: (0 минут 0.081 секунд)
Связанные примеры
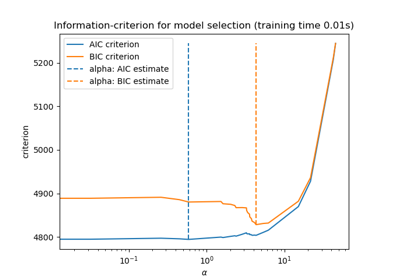
Выбор модели Lasso: AIC-BIC / перекрёстная проверка
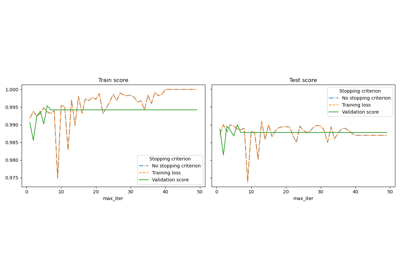
Ранняя остановка стохастического градиентного спуска