Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Аппроксимация кривой с использованием байесовской гребневой регрессии#
Вычисляет байесовскую гребневую регрессию синусоид.
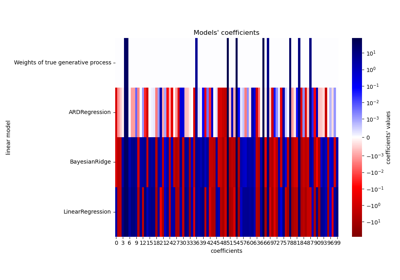
См. Байесовская гребневая регрессия Первые три столбца показывают прогнозируемую вероятность для различных значений двух признаков. Круглые маркеры представляют тестовые данные, которые были предсказаны как принадлежащие этому классу.
В общем случае, при подгонке кривой полиномом с помощью байесовской гребневой регрессии, выбор начальных значений параметров регуляризации (alpha, lambda) может быть важен. Это связано с тем, что параметры регуляризации определяются итерационной процедурой, зависящей от начальных значений.
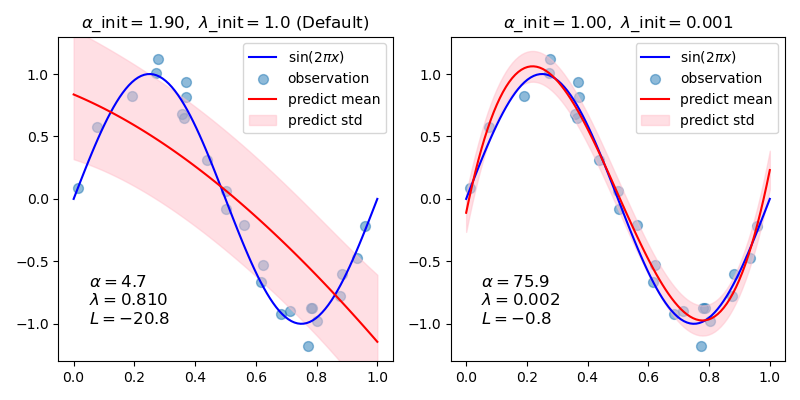
В этом примере синусоида аппроксимируется полиномом с использованием разных пар начальных значений.
При начальных значениях по умолчанию (alpha_init = 1.90, lambda_init = 1.) смещение результирующей кривой велико, а дисперсия мала. Поэтому lambda_init должен быть относительно малым (1.e-3), чтобы уменьшить смещение.
Кроме того, оценивая логарифм маргинального правдоподобия (L) этих моделей, мы можем определить, какая из них лучше. Можно заключить, что модель с большим L более вероятна.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Генерация синусоидальных данных с шумом#
import numpy as np
def func(x):
return np.sin(2 * np.pi * x)
size = 25
rng = np.random.RandomState(1234)
x_train = rng.uniform(0.0, 1.0, size)
y_train = func(x_train) + rng.normal(scale=0.1, size=size)
x_test = np.linspace(0.0, 1.0, 100)
Подгонка кубическим полиномом#
from sklearn.linear_model import BayesianRidge
n_order = 3
X_train = np.vander(x_train, n_order + 1, increasing=True)
X_test = np.vander(x_test, n_order + 1, increasing=True)
reg = BayesianRidge(tol=1e-6, fit_intercept=False, compute_score=True)
Построение истинных и предсказанных кривых с логарифмическим маргинальным правдоподобием (L)#
import matplotlib.pyplot as plt
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
for i, ax in enumerate(axes):
# Bayesian ridge regression with different initial value pairs
if i == 0:
init = [1 / np.var(y_train), 1.0] # Default values
elif i == 1:
init = [1.0, 1e-3]
reg.set_params(alpha_init=init[0], lambda_init=init[1])
reg.fit(X_train, y_train)
ymean, ystd = reg.predict(X_test, return_std=True)
ax.plot(x_test, func(x_test), color="blue", label="sin($2\\pi x$)")
ax.scatter(x_train, y_train, s=50, alpha=0.5, label="observation")
ax.plot(x_test, ymean, color="red", label="predict mean")
ax.fill_between(
x_test, ymean - ystd, ymean + ystd, color="pink", alpha=0.5, label="predict std"
)
ax.set_ylim(-1.3, 1.3)
ax.legend()
title = "$\\alpha$_init$={:.2f},\\ \\lambda$_init$={}$".format(init[0], init[1])
if i == 0:
title += " (Default)"
ax.set_title(title, fontsize=12)
text = "$\\alpha={:.1f}$\n$\\lambda={:.3f}$\n$L={:.1f}$".format(
reg.alpha_, reg.lambda_, reg.scores_[-1]
)
ax.text(0.05, -1.0, text, fontsize=12)
plt.tight_layout()
plt.show()
Общее время выполнения скрипта: (0 минут 0.297 секунд)
Связанные примеры
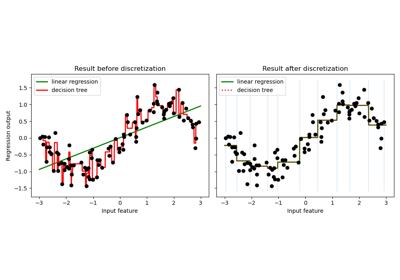
Использование KBinsDiscretizer для дискретизации непрерывных признаков