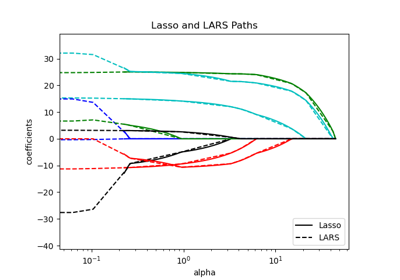
lasso_path#
- sklearn.linear_model.lasso_path(X, y, *, eps=0.001, n_alphas=100, альфы=None, precompute='auto', Xy=None, copy_X=True, coef_init=None, verbose=False, return_n_iter=False, положительный=False, **params)[источник]#
Вычислить путь Lasso с координатным спуском.
Функция оптимизации Lasso различается для одно- и многомерных выходов.
Для задач с одним выходом это:
(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1
Для многозадачных задач это:
(1 / (2 * n_samples)) * ||Y - XW||^2_Fro + alpha * ||W||_21
Где:
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
т.е. сумма норм каждой строки.
Подробнее в Руководство пользователя.
- Параметры:
- X{array-like, sparse matrix} формы (n_samples, n_features)
Обучающие данные. Передавайте непосредственно как данные с порядком хранения Fortran, чтобы избежать ненужного дублирования памяти. Если
yявляется моно-выходным, тогдаXможет быть разреженным.- y{array-like, sparse matrix} формы (n_samples,) или (n_samples, n_targets)
Целевые значения.
- epsfloat, по умолчанию=1e-3
Длина пути.
eps=1e-3означает, чтоalpha_min / alpha_max = 1e-3.- n_alphasint, по умолчанию=100
Количество альфа вдоль пути регуляризации.
- альфыarray-like, default=None
Список альфа, для которых вычисляются модели. Если
Noneпараметры alphas устанавливаются автоматически.- precompute'auto', bool или массив формы (n_features, n_features), по умолчанию='auto'
Использовать ли предварительно вычисленную матрицу Грама для ускорения вычислений. Если установлено в
'auto'пусть мы решим. Матрица Грама также может быть передана в качестве аргумента.- Xyarray-like формы (n_features,) или (n_features, n_targets), default=None
Xy = np.dot(X.T, y), который может быть предварительно вычислен. Это полезно только когда матрица Грама предварительно вычислена.
- copy_Xbool, по умолчанию=True
Если
True, X будет скопирован; иначе, он может быть перезаписан.- coef_initarray-like формы (n_features, ), по умолчанию=None
Начальные значения коэффициентов.
- verbosebool или int, по умолчанию=False
Уровень детализации вывода.
- return_n_iterbool, по умолчанию=False
Возвращать ли количество итераций или нет.
- положительныйbool, по умолчанию=False
Если установлено в True, заставляет коэффициенты быть положительными. (Разрешено только когда
y.ndim == 1).- **paramskwargs
Аргументы ключевых слов, передаваемые решателю координатного спуска.
- Возвращает:
- альфыndarray формы (n_alphas,)
Значения alphas вдоль пути, по которому вычисляются модели.
- coefsndarray формы (n_features, n_alphas) или (n_targets, n_features, n_alphas)
Коэффициенты вдоль пути.
- dual_gapsndarray формы (n_alphas,)
Двойные разрывы в конце оптимизации для каждого альфа.
- n_itersсписок целых чисел
Количество итераций, выполненных оптимизатором координатного спуска для достижения указанного допуска для каждого альфа.
Смотрите также
lars_pathВычислить путь регрессии наименьших углов или Lasso с использованием алгоритма LARS.
LassoLasso — это линейная модель, которая оценивает разреженные коэффициенты.
LassoLarsМодель Lasso, обученная с использованием метода наименьших углов, также известного как Lars.
LassoCVЛассо линейная модель с итеративной подгонкой вдоль пути регуляризации.
LassoLarsCVПерекрёстно проверенный Lasso с использованием алгоритма LARS.
sklearn.decomposition.sparse_encodeОценщик, который может использоваться для преобразования сигналов в разреженную линейную комбинацию атомов из фиксированного.
Примечания
Пример см. в examples/linear_model/plot_lasso_lasso_lars_elasticnet_path.py.
Чтобы избежать ненужного дублирования памяти, аргумент X метода fit должен передаваться напрямую как массив numpy с порядком Fortran.
Обратите внимание, что в некоторых случаях решатель Lars может быть значительно быстрее для реализации этой функциональности. В частности, линейная интерполяция может использоваться для получения коэффициентов модели между значениями, выводимыми lars_path.
Базовый решатель координатного спуска использует правила безопасного скрининга с зазором для ускорения времени подгонки, см. Руководство пользователя по координатному спуску.
Примеры
Сравнение lasso_path и lars_path с интерполяцией:
>>> import numpy as np >>> from sklearn.linear_model import lasso_path >>> X = np.array([[1, 2, 3.1], [2.3, 5.4, 4.3]]).T >>> y = np.array([1, 2, 3.1]) >>> # Use lasso_path to compute a coefficient path >>> _, coef_path, _ = lasso_path(X, y, alphas=[5., 1., .5]) >>> print(coef_path) [[0. 0. 0.46874778] [0.2159048 0.4425765 0.23689075]]
>>> # Now use lars_path and 1D linear interpolation to compute the >>> # same path >>> from sklearn.linear_model import lars_path >>> alphas, active, coef_path_lars = lars_path(X, y, method='lasso') >>> from scipy import interpolate >>> coef_path_continuous = interpolate.interp1d(alphas[::-1], ... coef_path_lars[:, ::-1]) >>> print(coef_path_continuous([5., 1., .5])) [[0. 0. 0.46915237] [0.2159048 0.4425765 0.23668876]]