Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Компрессионное зондирование: реконструкция томографии с априорным распределением L1 (Lasso)#

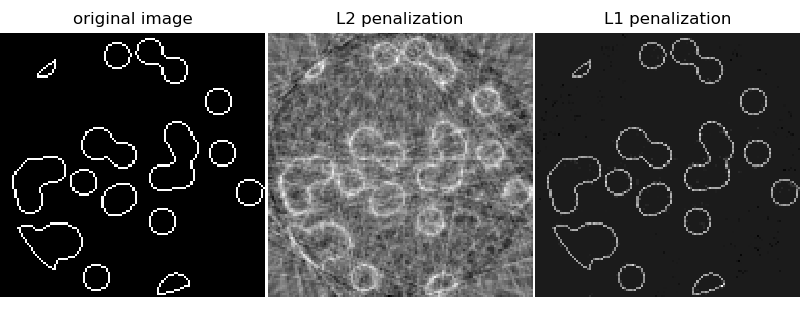
Этот пример показывает восстановление изображения из набора параллельных проекций, полученных под разными углами. Такой набор данных получается в компьютерная томография (CT).

Без какой-либо априорной информации о выборке, количество проекций, необходимых для восстановления изображения, имеет порядок линейного размера l изображения (в пикселях). Для простоты мы рассматриваем здесь разреженное изображение, где только пиксели на границах объектов имеют ненулевое значение. Такие данные могут соответствовать, например, клеточному материалу. Однако обратите внимание, что большинство изображений разрежены в другом базисе, таком как вейвлеты Хаара. Только l/7 проекции получены, поэтому необходимо использовать доступную априорную информацию о выборке (её разреженность): это пример компрессионное зондирование.

Операция томографической проекции является линейным преобразованием. В дополнение к члену соответствия данным, соответствующему линейной регрессии, мы штрафуем L1-норму изображения для учета его разреженности. Полученная оптимизационная задача называется Lasso. Мы используем класс Lasso, который использует алгоритм координатного спуска. Важно, что эта реализация более вычислительно эффективна на разреженной матрице, чем оператор проекции, используемый здесь.

Реконструкция с L1-штрафом дает результат с нулевой ошибкой (все пиксели успешно помечены как 0 или 1), даже если в проекции был добавлен шум. Для сравнения, L2-штраф (Ridge) даёт большое количество ошибок маркировки для пикселей. Важные артефакты наблюдаются на восстановленном изображении, в отличие от L1-штрафа. Обратите внимание, в частности, на круговой артефакт, разделяющий пиксели в углах, которые внесли вклад в меньшее количество проекций, чем центральный диск.

original image, L2 penalization, L1 penalization

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
from scipy import ndimage, sparse

from sklearn.linear_model import Lasso, Ridge


def _weights(x, dx=1, orig=0):
    x = np.ravel(x)
    floor_x = np.floor((x - orig) / dx).astype(np.int64)
    alpha = (x - orig - floor_x * dx) / dx
    return np.hstack((floor_x, floor_x + 1)), np.hstack((1 - alpha, alpha))


def _generate_center_coordinates(l_x):
    X, Y = np.mgrid[:l_x, :l_x].astype(np.float64)
    center = l_x / 2.0
    X += 0.5 - center
    Y += 0.5 - center
    return X, Y


def build_projection_operator(l_x, n_dir):
    """Compute the tomography design matrix.

    Parameters
    ----------

    l_x : int
        linear size of image array

    n_dir : int
        number of angles at which projections are acquired.

    Returns
    -------
    p : sparse matrix of shape (n_dir l_x, l_x**2)
    """
    X, Y = _generate_center_coordinates(l_x)
    angles = np.linspace(0, np.pi, n_dir, endpoint=False)
    data_inds, weights, camera_inds = [], [], []
    data_unravel_indices = np.arange(l_x**2)
    data_unravel_indices = np.hstack((data_unravel_indices, data_unravel_indices))
    for i, angle in enumerate(angles):
        Xrot = np.cos(angle) * X - np.sin(angle) * Y
        inds, w = _weights(Xrot, dx=1, orig=X.min())
        mask = np.logical_and(inds >= 0, inds < l_x)
        weights += list(w[mask])
        camera_inds += list(inds[mask] + i * l_x)
        data_inds += list(data_unravel_indices[mask])
    proj_operator = sparse.coo_matrix((weights, (camera_inds, data_inds)))
    return proj_operator


def generate_synthetic_data():
    """Synthetic binary data"""
    rs = np.random.RandomState(0)
    n_pts = 36
    x, y = np.ogrid[0:l, 0:l]
    mask_outer = (x - l / 2.0) ** 2 + (y - l / 2.0) ** 2 < (l / 2.0) ** 2
    mask = np.zeros((l, l))
    points = l * rs.rand(2, n_pts)
    mask[(points[0]).astype(int), (points[1]).astype(int)] = 1
    mask = ndimage.gaussian_filter(mask, sigma=l / n_pts)
    res = np.logical_and(mask > mask.mean(), mask_outer)
    return np.logical_xor(res, ndimage.binary_erosion(res))


# Generate synthetic images, and projections
l = 128
proj_operator = build_projection_operator(l, l // 7)
data = generate_synthetic_data()
proj = proj_operator @ data.ravel()[:, np.newaxis]
proj += 0.15 * np.random.randn(*proj.shape)

# Reconstruction with L2 (Ridge) penalization
rgr_ridge = Ridge(alpha=0.2)
rgr_ridge.fit(proj_operator, proj.ravel())
rec_l2 = rgr_ridge.coef_.reshape(l, l)

# Reconstruction with L1 (Lasso) penalization
# the best value of alpha was determined using cross validation
# with LassoCV
rgr_lasso = Lasso(alpha=0.001)
rgr_lasso.fit(proj_operator, proj.ravel())
rec_l1 = rgr_lasso.coef_.reshape(l, l)

plt.figure(figsize=(8, 3.3))
plt.subplot(131)
plt.imshow(data, cmap=plt.cm.gray, interpolation="nearest")
plt.axis("off")
plt.title("original image")
plt.subplot(132)
plt.imshow(rec_l2, cmap=plt.cm.gray, interpolation="nearest")
plt.title("L2 penalization")
plt.axis("off")
plt.subplot(133)
plt.imshow(rec_l1, cmap=plt.cm.gray, interpolation="nearest")
plt.title("L1 penalization")
plt.axis("off")

plt.subplots_adjust(hspace=0.01, wspace=0.01, top=1, bottom=0, left=0, right=1)

plt.show()