Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

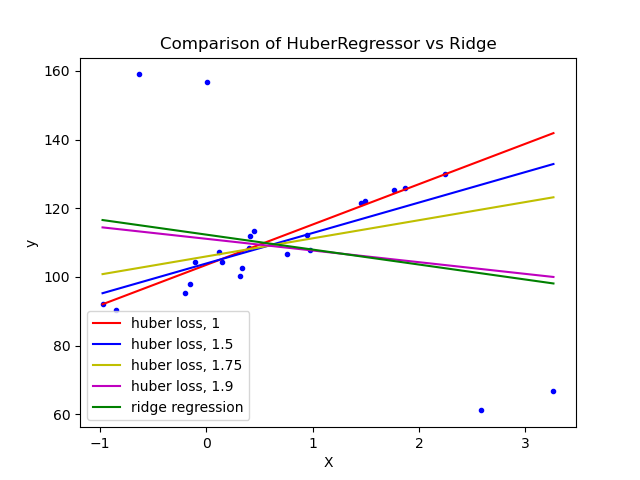
HuberRegressor против Ridge на наборе данных с сильными выбросами#

Обучите Ridge и HuberRegressor на наборе данных с выбросами.

Пример показывает, что предсказания в ridge сильно зависят от выбросов, присутствующих в наборе данных. Регрессор Huber менее подвержен влиянию выбросов, поскольку модель использует линейную функцию потерь для них. По мере увеличения параметра epsilon для регрессора Huber функция принятия решений приближается к таковой у ridge.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_regression
from sklearn.linear_model import HuberRegressor, Ridge

# Generate toy data.
rng = np.random.RandomState(0)
X, y = make_regression(
    n_samples=20, n_features=1, random_state=0, noise=4.0, bias=100.0
)

# Add four strong outliers to the dataset.
X_outliers = rng.normal(0, 0.5, size=(4, 1))
y_outliers = rng.normal(0, 2.0, size=4)
X_outliers[:2, :] += X.max() + X.mean() / 4.0
X_outliers[2:, :] += X.min() - X.mean() / 4.0
y_outliers[:2] += y.min() - y.mean() / 4.0
y_outliers[2:] += y.max() + y.mean() / 4.0
X = np.vstack((X, X_outliers))
y = np.concatenate((y, y_outliers))
plt.plot(X, y, "b.")

# Fit the huber regressor over a series of epsilon values.
colors = ["r-", "b-", "y-", "m-"]

x = np.linspace(X.min(), X.max(), 7)
epsilon_values = [1, 1.5, 1.75, 1.9]
for k, epsilon in enumerate(epsilon_values):
    huber = HuberRegressor(alpha=0.0, epsilon=epsilon)
    huber.fit(X, y)
    coef_ = huber.coef_ * x + huber.intercept_
    plt.plot(x, coef_, colors[k], label="huber loss, %s" % epsilon)

# Fit a ridge regressor to compare it to huber regressor.
ridge = Ridge(alpha=0.0, random_state=0)
ridge.fit(X, y)
coef_ridge = ridge.coef_
coef_ = ridge.coef_ * x + ridge.intercept_
plt.plot(x, coef_, "g-", label="ridge regression")

plt.title("Comparison of HuberRegressor vs Ridge")
plt.xlabel("X")
plt.ylabel("y")
plt.legend(loc=0)
plt.show()