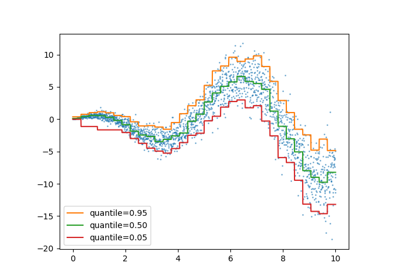
Квантильная регрессия

Этот пример иллюстрирует, как квантильная регрессия может предсказывать нетривиальные условные квантили.

Левая фигура показывает случай, когда распределение ошибок нормальное, но имеет непостоянную дисперсию, т.е. гетероскедастичность.

Правая фигура показывает пример асимметричного распределения ошибок, а именно распределение Парето.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Генерация набора данных

Чтобы проиллюстрировать поведение квантильной регрессии, мы сгенерируем два синтетических набора данных. Истинные генеративные случайные процессы для обоих наборов данных будут состоять из одного и того же ожидаемого значения с линейной зависимостью от одного признака x.

import numpy as np

rng = np.random.RandomState(42)
x = np.linspace(start=0, stop=10, num=100)
X = x[:, np.newaxis]
y_true_mean = 10 + 0.5 * x

Мы создадим две последующие задачи, изменив распределение целевой переменной y сохраняя то же математическое ожидание:

• в первом случае добавляется гетероскедастический нормальный шум;

• во втором случае добавляется асимметричный шум Парето.

y_normal = y_true_mean + rng.normal(loc=0, scale=0.5 + 0.5 * x, size=x.shape[0])
a = 5
y_pareto = y_true_mean + 10 * (rng.pareto(a, size=x.shape[0]) - 1 / (a - 1))

Давайте сначала визуализируем наборы данных, а также распределение остатков y - mean(y).

import matplotlib.pyplot as plt

_, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 11), sharex="row", sharey="row")

axs[0, 0].plot(x, y_true_mean, label="True mean")
axs[0, 0].scatter(x, y_normal, color="black", alpha=0.5, label="Observations")
axs[1, 0].hist(y_true_mean - y_normal, edgecolor="black")


axs[0, 1].plot(x, y_true_mean, label="True mean")
axs[0, 1].scatter(x, y_pareto, color="black", alpha=0.5, label="Observations")
axs[1, 1].hist(y_true_mean - y_pareto, edgecolor="black")

axs[0, 0].set_title("Dataset with heteroscedastic Normal distributed targets")
axs[0, 1].set_title("Dataset with asymmetric Pareto distributed target")
axs[1, 0].set_title(
    "Residuals distribution for heteroscedastic Normal distributed targets"
)
axs[1, 1].set_title("Residuals distribution for asymmetric Pareto distributed target")
axs[0, 0].legend()
axs[0, 1].legend()
axs[0, 0].set_ylabel("y")
axs[1, 0].set_ylabel("Counts")
axs[0, 1].set_xlabel("x")
axs[0, 0].set_xlabel("x")
axs[1, 0].set_xlabel("Residuals")
_ = axs[1, 1].set_xlabel("Residuals")

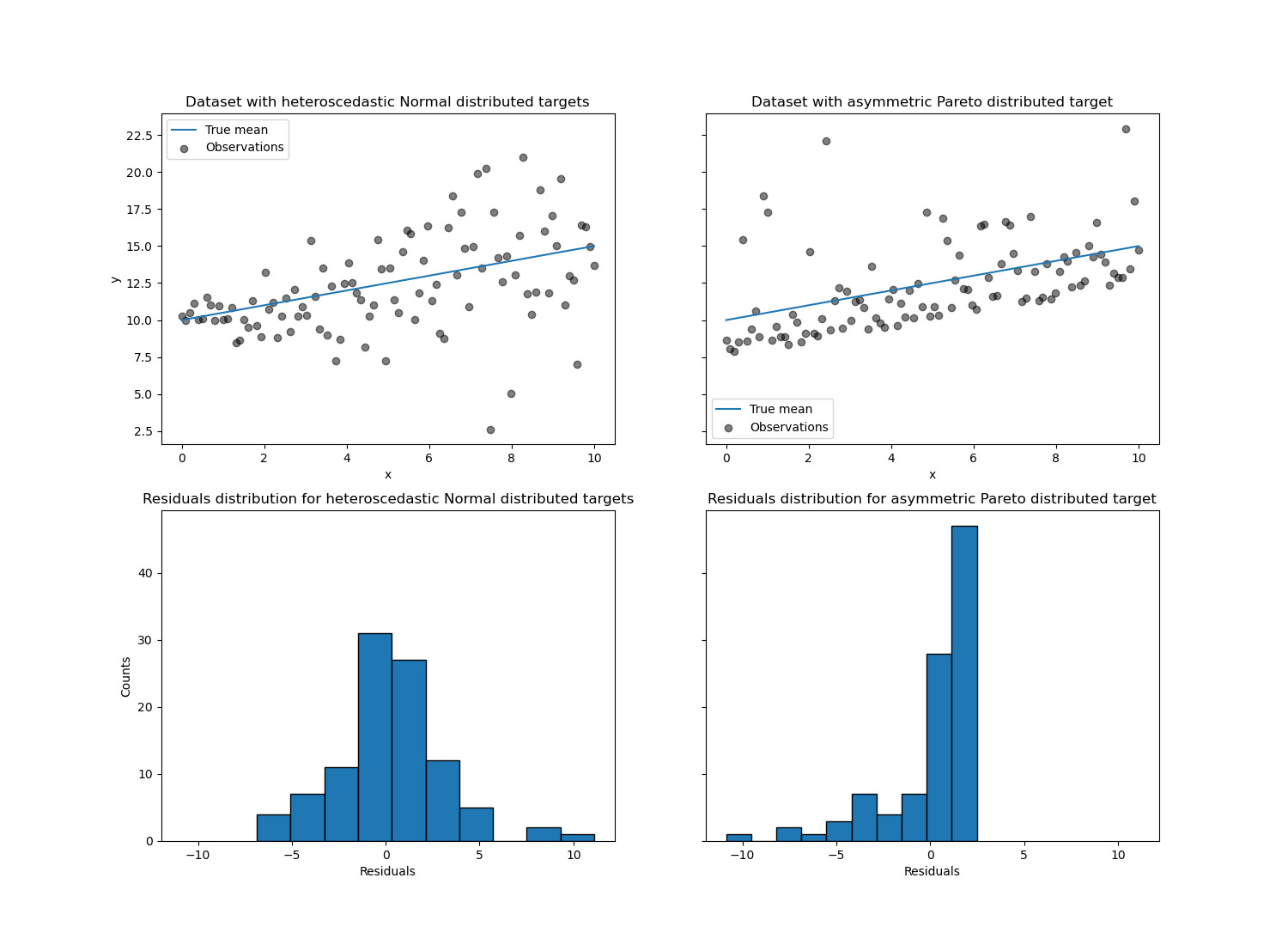
С гетероскедастичным нормально распределенным целевым значением мы наблюдаем, что дисперсия шума увеличивается, когда значение признака x является возрастающей.

При асимметричном распределении Парето целевой переменной мы наблюдаем, что положительные остатки ограничены.

Эти типы зашумленных целей делают оценку через LinearRegression менее эффективен, т.е. нам нужно больше данных для получения стабильных результатов, и, кроме того, большие выбросы могут сильно повлиять на подобранные коэффициенты. (Другими словами: в условиях постоянной дисперсии оценки обычного метода наименьших квадратов сходятся к true коэффициенты с увеличением размера выборки.)

В этой асимметричной настройке медиана или различные квантили дают дополнительные сведения. Кроме того, оценка медианы гораздо более устойчива к выбросам и распределениям с тяжёлыми хвостами. Но обратите внимание, что экстремальные квантили оцениваются очень небольшим количеством точек данных. 95% квантиль оценивается примерно по 5% наибольших значений и поэтому также немного чувствителен к выбросам.

В оставшейся части этого руководства мы покажем, как QuantileRegressor могут использоваться на практике и дают интуитивное представление о свойствах обученных моделей. Наконец, мы сравним оба QuantileRegressor и LinearRegression.

Обучение QuantileRegressor

В этом разделе мы хотим оценить условную медиану, а также низкий и высокий квантили, фиксированные на 5% и 95% соответственно. Таким образом, мы получим три линейные модели, по одной для каждого квантиля.

Мы будем использовать квантили 5% и 95%, чтобы найти выбросы в обучающей выборке за пределами центрального 90% интервала.

from sklearn.linear_model import QuantileRegressor

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0)
    y_pred = qr.fit(X, y_normal).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_normal
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_normal
        )

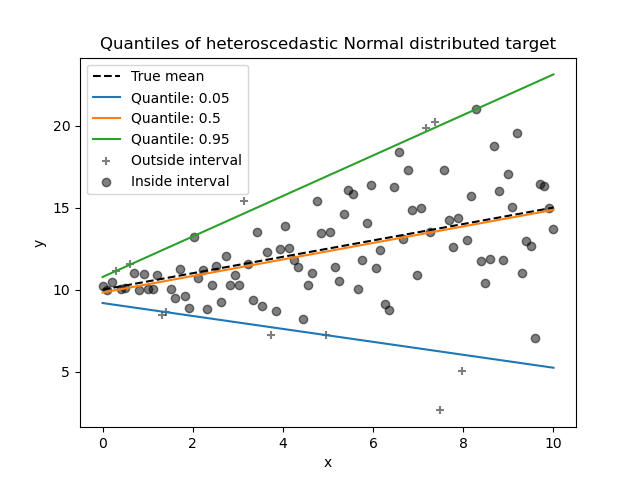
Теперь мы можем построить три линейные модели и выделить образцы, находящиеся в центральном 90% интервале, от образцов вне этого интервала.

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"Quantile: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_normal[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="Outside interval",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_normal[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="Inside interval",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of heteroscedastic Normal distributed target")

был перемещен из x.

Чтобы получить дополнительное представление о значении оценок 5% и 95% квантилей, можно подсчитать количество образцов выше и ниже предсказанных квантилей (представленных крестиком на графике выше), учитывая, что у нас всего 100 образцов.

Мы можем повторить тот же эксперимент, используя асимметрично распределённую по Парето целевую переменную.

quantiles = [0.05, 0.5, 0.95]
predictions = {}
out_bounds_predictions = np.zeros_like(y_true_mean, dtype=np.bool_)
for quantile in quantiles:
    qr = QuantileRegressor(quantile=quantile, alpha=0)
    y_pred = qr.fit(X, y_pareto).predict(X)
    predictions[quantile] = y_pred

    if quantile == min(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred >= y_pareto
        )
    elif quantile == max(quantiles):
        out_bounds_predictions = np.logical_or(
            out_bounds_predictions, y_pred <= y_pareto
        )

plt.plot(X, y_true_mean, color="black", linestyle="dashed", label="True mean")

for quantile, y_pred in predictions.items():
    plt.plot(X, y_pred, label=f"Quantile: {quantile}")

plt.scatter(
    x[out_bounds_predictions],
    y_pareto[out_bounds_predictions],
    color="black",
    marker="+",
    alpha=0.5,
    label="Outside interval",
)
plt.scatter(
    x[~out_bounds_predictions],
    y_pareto[~out_bounds_predictions],
    color="black",
    alpha=0.5,
    label="Inside interval",
)

plt.legend()
plt.xlabel("x")
plt.ylabel("y")
_ = plt.title("Quantiles of asymmetric Pareto distributed target")

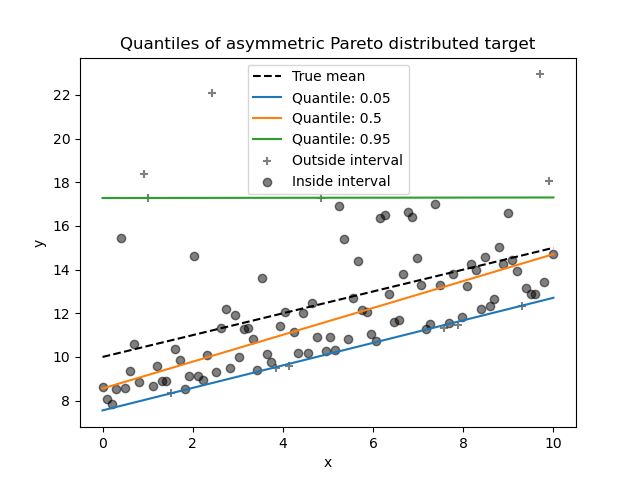
Из-за асимметрии распределения шума мы наблюдаем, что истинное среднее и оценённая условная медиана различаются. Мы также наблюдаем, что каждая квантильная модель имеет разные параметры для лучшего соответствия желаемому квантилю. Обратите внимание, что в идеале все квантили были бы параллельны в этом случае, что стало бы более заметным с большим количеством точек данных или менее экстремальными квантилями, например 10% и 90%.

Сравнение QuantileRegressor и LinearRegression

В этом разделе мы подробно остановимся на различиях в функциях потерь, которые QuantileRegressor и LinearRegression минимизируют.

Действительно, LinearRegression является методом наименьших квадратов, минимизирующим среднеквадратичную ошибку (MSE) между обучающими и предсказанными целями. В отличие от QuantileRegressor с quantile=0.5 минимизирует среднюю абсолютную ошибку (MAE) вместо этого.

Почему это важно? Функции потерь определяют, что именно модель стремится предсказать, см. руководство пользователя по выбору функции оценки. Короче говоря, модель, минимизирующая MSE, предсказывает среднее (математическое ожидание), а модель, минимизирующая MAE, предсказывает медиану.

Вычислим ошибки обучения таких моделей в терминах средней квадратичной ошибки и средней абсолютной ошибки. Мы будем использовать асимметричное распределение Парето для цели, чтобы сделать это более интересным, так как среднее и медиана не равны.

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

linear_regression = LinearRegression()
quantile_regression = QuantileRegressor(quantile=0.5, alpha=0)

y_pred_lr = linear_regression.fit(X, y_pareto).predict(X)
y_pred_qr = quantile_regression.fit(X, y_pareto).predict(X)

print(
    "Training error (in-sample performance)\n"
    f"{'model':<20}   MAE   MSE\n"
    f"{linear_regression.__class__.__name__:<20} "
    f"{mean_absolute_error(y_pareto, y_pred_lr):5.3f} "
    f"{mean_squared_error(y_pareto, y_pred_lr):5.3f}\n"
    f"{quantile_regression.__class__.__name__:<20} "
    f"{mean_absolute_error(y_pareto, y_pred_qr):5.3f} "
    f"{mean_squared_error(y_pareto, y_pred_qr):5.3f}"
)

Training error (in-sample performance)
model                  MAE   MSE
LinearRegression     1.805 6.486
QuantileRegressor    1.670 7.025

На обучающем наборе мы видим, что MAE ниже для QuantileRegressor чем LinearRegression. В отличие от этого, MSE ниже для LinearRegression чем QuantileRegressor. Эти результаты подтверждают, что MAE является функцией потерь, минимизируемой QuantileRegressor в то время как MSE - это минимизируемая функция потерь LinearRegression.

Мы можем провести аналогичную оценку, посмотрев на тестовую ошибку, полученную с помощью перекрестной проверки.

from sklearn.model_selection import cross_validate

cv_results_lr = cross_validate(
    linear_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
cv_results_qr = cross_validate(
    quantile_regression,
    X,
    y_pareto,
    cv=3,
    scoring=["neg_mean_absolute_error", "neg_mean_squared_error"],
)
print(
    "Test error (cross-validated performance)\n"
    f"{'model':<20}   MAE   MSE\n"
    f"{linear_regression.__class__.__name__:<20} "
    f"{-cv_results_lr['test_neg_mean_absolute_error'].mean():5.3f} "
    f"{-cv_results_lr['test_neg_mean_squared_error'].mean():5.3f}\n"
    f"{quantile_regression.__class__.__name__:<20} "
    f"{-cv_results_qr['test_neg_mean_absolute_error'].mean():5.3f} "
    f"{-cv_results_qr['test_neg_mean_squared_error'].mean():5.3f}"
)

Test error (cross-validated performance)
model                  MAE   MSE
LinearRegression     1.732 6.690
QuantileRegressor    1.679 7.129

Мы приходим к аналогичным выводам при оценке вне выборки.

Связанные примеры

Интервалы прогнозирования для регрессии градиентного бустинга

Интервалы прогнозирования для регрессии градиентного бустинга

Основные изменения в выпуске scikit-learn 1.1

Основные изменения в выпуске scikit-learn 1.1

Лаггированные признаки для прогнозирования временных рядов

Лаггированные признаки для прогнозирования временных рядов

Демонстрация предположений k-means

Демонстрация предположений k-means