Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Полиномиальная и сплайновая интерполяция#

Этот пример демонстрирует, как аппроксимировать функцию полиномами до степени degree с использованием гребневой регрессии. Мы показываем два различных способа, заданных n_samples из 1d точек x_i:

PolynomialFeatures генерирует все мономы до degree. Это даёт нам так называемую матрицу Вандермонда с n_samples строк и degree + 1 столбцы:
```
[[1, x_0, x_0 ** 2, x_0 ** 3, ..., x_0 ** degree],
 [1, x_1, x_1 ** 2, x_1 ** 3, ..., x_1 ** degree],
 ...]
```
Интуитивно эту матрицу можно интерпретировать как матрицу псевдопризнаков (точки, возведенные в некоторую степень). Матрица похожа на (но отличается от) матрицы, индуцированной полиномиальным ядром.
SplineTransformer генерирует базисные функции B-сплайна. Базисная функция B-сплайна — это кусочно-полиномиальная функция степени degree который не равен нулю только между degree+1 последовательные узлы. Учитывая n_knots количество узлов, это приводит к матрице n_samples строк и n_knots + degree - 1 столбцы:
```
[[basis_1(x_0), basis_2(x_0), ...],
 [basis_1(x_1), basis_2(x_1), ...],
 ...]
```

Этот пример показывает, что эти два преобразователя хорошо подходят для моделирования нелинейных эффектов с линейной моделью, используя конвейер для добавления нелинейных признаков. Ядерные методы расширяют эту идею и могут создавать очень высокоразмерные (даже бесконечномерные) пространства признаков.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures, SplineTransformer

Мы начинаем с определения функции, которую намерены аппроксимировать, и подготовки её построения.

def f(x):
    """Function to be approximated by polynomial interpolation."""
    return x * np.sin(x)


# whole range we want to plot
x_plot = np.linspace(-1, 11, 100)

Чтобы сделать это интересным, мы даем только небольшое подмножество точек для обучения.

x_train = np.linspace(0, 10, 100)
rng = np.random.RandomState(0)
x_train = np.sort(rng.choice(x_train, size=20, replace=False))
y_train = f(x_train)

# create 2D-array versions of these arrays to feed to transformers
X_train = x_train[:, np.newaxis]
X_plot = x_plot[:, np.newaxis]

Теперь мы готовы создать полиномиальные признаки и сплайны, обучить на тренировочных точках и показать, насколько хорошо они интерполируют.

# plot function
lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(
    color=["black", "teal", "yellowgreen", "gold", "darkorange", "tomato"]
)
ax.plot(x_plot, f(x_plot), linewidth=lw, label="ground truth")

# plot training points
ax.scatter(x_train, y_train, label="training points")

# polynomial features
for degree in [3, 4, 5]:
    model = make_pipeline(PolynomialFeatures(degree), Ridge(alpha=1e-3))
    model.fit(X_train, y_train)
    y_plot = model.predict(X_plot)
    ax.plot(x_plot, y_plot, label=f"degree {degree}")

# B-spline with 4 + 3 - 1 = 6 basis functions
model = make_pipeline(SplineTransformer(n_knots=4, degree=3), Ridge(alpha=1e-3))
model.fit(X_train, y_train)

y_plot = model.predict(X_plot)
ax.plot(x_plot, y_plot, label="B-spline")
ax.legend(loc="lower center")
ax.set_ylim(-20, 10)
plt.show()

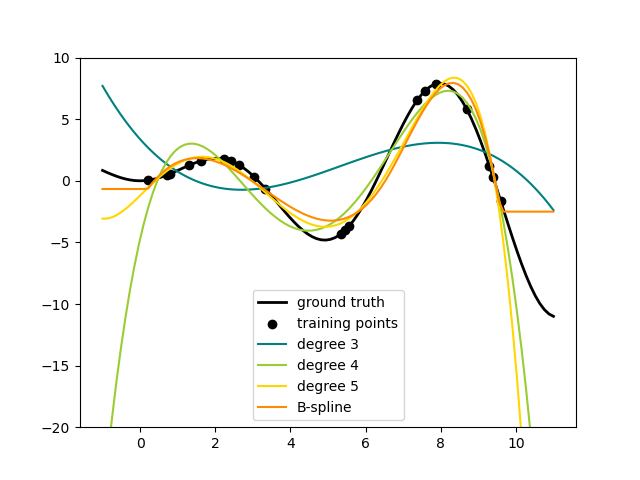
Это хорошо показывает, что полиномы более высокой степени могут лучше соответствовать данным. Но в то же время слишком высокие степени могут демонстрировать нежелательное осцилляторное поведение и особенно опасны для экстраполяции за пределы диапазона подогнанных данных. Это преимущество B-сплайнов. Обычно они соответствуют данным так же хорошо, как полиномы, и демонстрируют очень хорошее и плавное поведение. У них также есть хорошие возможности для управления экстраполяцией, которая по умолчанию продолжается с постоянным значением. Обратите внимание, что чаще всего вы бы скорее увеличили количество узлов, но сохранили degree=3.

Чтобы дать больше информации о сгенерированных базисах признаков, мы строим все столбцы обоих преобразователей отдельно.

fig, axes = plt.subplots(ncols=2, figsize=(16, 5))
pft = PolynomialFeatures(degree=3).fit(X_train)
axes[0].plot(x_plot, pft.transform(X_plot))
axes[0].legend(axes[0].lines, [f"degree {n}" for n in range(4)])
axes[0].set_title("PolynomialFeatures")

splt = SplineTransformer(n_knots=4, degree=3).fit(X_train)
axes[1].plot(x_plot, splt.transform(X_plot))
axes[1].legend(axes[1].lines, [f"spline {n}" for n in range(6)])
axes[1].set_title("SplineTransformer")

# plot knots of spline
knots = splt.bsplines_[0].t
axes[1].vlines(knots[3:-3], ymin=0, ymax=0.8, linestyles="dashed")
plt.show()

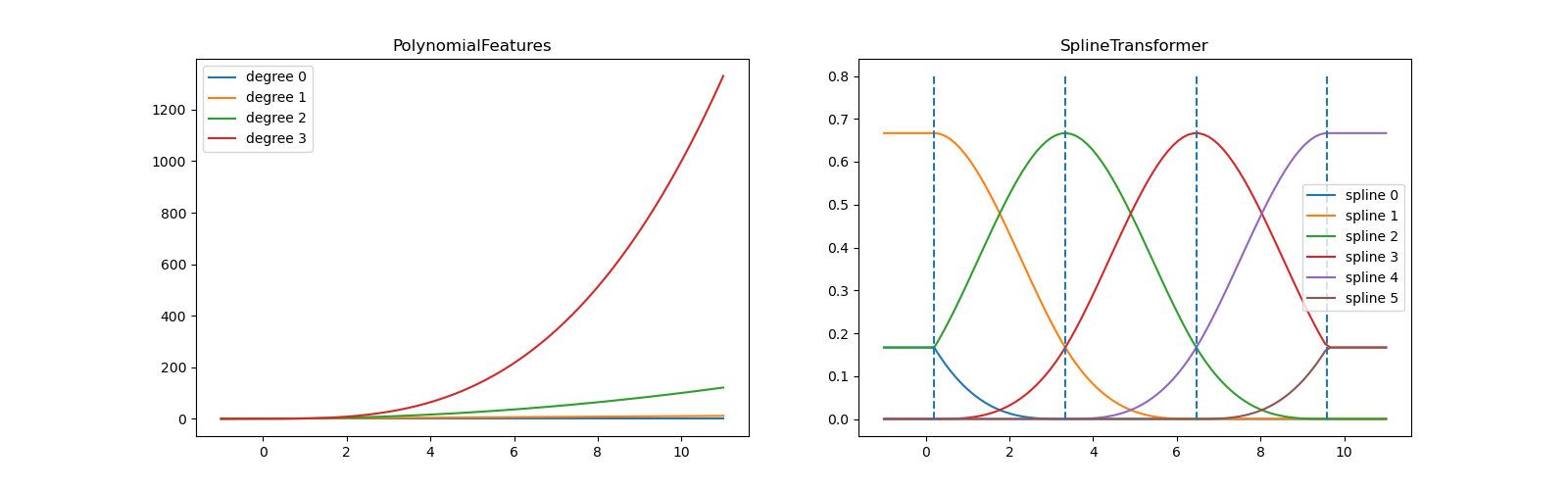
На левом графике мы распознаём линии, соответствующие простым мономам из x**0 to x**3. На правом рисунке мы видим шесть базисных функций B-сплайна degree=3 а также четыре позиции узлов, которые были выбраны во время fit. Обратите внимание, что есть degree количество дополнительных узлов слева и справа от подогнанного интервала. Они существуют по техническим причинам, поэтому мы воздерживаемся от их отображения. Каждая базисная функция имеет локальную поддержку и продолжается как константа за пределами подогнанного диапазона. Это экстраполирующее поведение может быть изменено аргументом extrapolation.

Периодические сплайны#

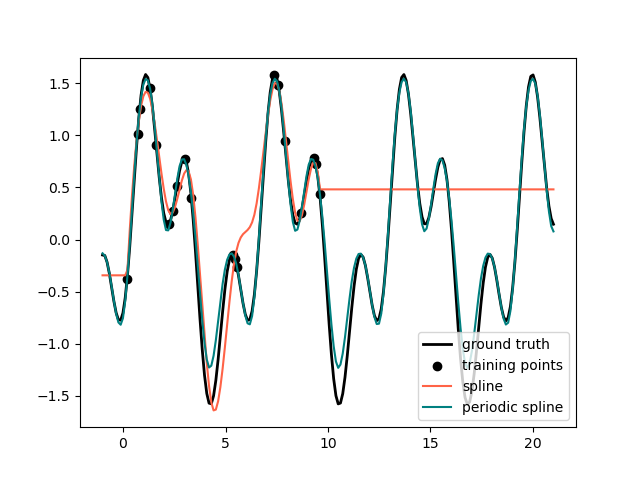
В предыдущем примере мы увидели ограничения полиномов и сплайнов для экстраполяции за пределы диапазона обучающих наблюдений. В некоторых случаях, например, с сезонными эффектами, мы ожидаем периодического продолжения основного сигнала. Такие эффекты можно моделировать с помощью периодических сплайнов, которые имеют одинаковое значение функции и одинаковые производные в первой и последней узловых точках. В следующем случае мы показываем, как периодические сплайны обеспечивают лучшее соответствие как внутри, так и за пределами диапазона обучающих данных, учитывая дополнительную информацию о периодичности. Период сплайнов — это расстояние между первой и последней узловыми точками, которое мы указываем вручную.

Периодические сплайны также могут быть полезны для естественно периодических признаков (таких как день года), поскольку гладкость на граничных узлах предотвращает скачок в преобразованных значениях (например, с 31 декабря на 1 января). Для таких естественно периодических признаков или, в более общем случае, признаков, где период известен, рекомендуется явно передавать эту информацию в SplineTransformer установив узлы вручную.

def g(x):
    """Function to be approximated by periodic spline interpolation."""
    return np.sin(x) - 0.7 * np.cos(x * 3)


y_train = g(x_train)

# Extend the test data into the future:
x_plot_ext = np.linspace(-1, 21, 200)
X_plot_ext = x_plot_ext[:, np.newaxis]

lw = 2
fig, ax = plt.subplots()
ax.set_prop_cycle(color=["black", "tomato", "teal"])
ax.plot(x_plot_ext, g(x_plot_ext), linewidth=lw, label="ground truth")
ax.scatter(x_train, y_train, label="training points")

for transformer, label in [
    (SplineTransformer(degree=3, n_knots=10), "spline"),
    (
        SplineTransformer(
            degree=3,
            knots=np.linspace(0, 2 * np.pi, 10)[:, None],
            extrapolation="periodic",
        ),
        "periodic spline",
    ),
]:
    model = make_pipeline(transformer, Ridge(alpha=1e-3))
    model.fit(X_train, y_train)
    y_plot_ext = model.predict(X_plot_ext)
    ax.plot(x_plot_ext, y_plot_ext, label=label)

ax.legend()
fig.show()

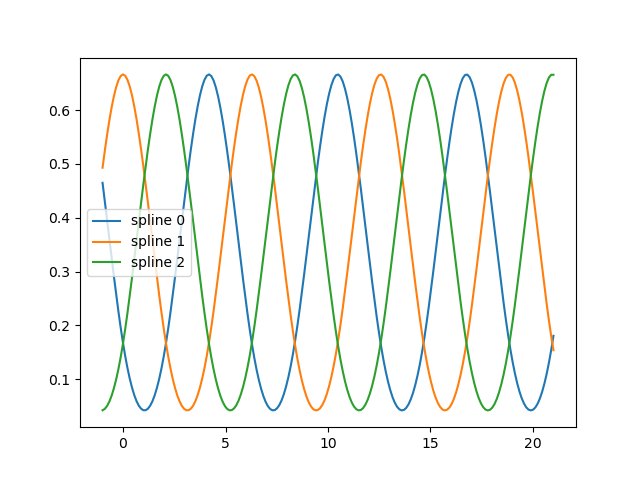
fig, ax = plt.subplots()
knots = np.linspace(0, 2 * np.pi, 4)
splt = SplineTransformer(knots=knots[:, None], degree=3, extrapolation="periodic").fit(
    X_train
)
ax.plot(x_plot_ext, splt.transform(X_plot_ext))
ax.legend(ax.lines, [f"spline {n}" for n in range(3)])
plt.show()