Границы решений мультиномиальной и логистической регрессии One-vs-Rest

Этот пример сравнивает границы решений мультиномиальной и one-vs-rest логистической регрессии на 2D наборе данных с тремя классами.

Мы проводим сравнение границ решений обоих методов, что эквивалентно вызову метода predict. Кроме того, мы строим гиперплоскости, которые соответствуют линии, когда оценка вероятности для класса равна 0.5.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

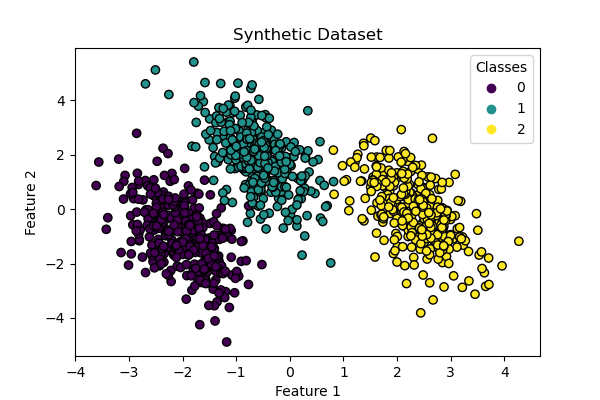
Генерация набора данных

Мы генерируем синтетический набор данных, используя make_blobs функция. Набор данных состоит из 1000 выборок из трех разных классов, центрированных вокруг [-5, 0], [0, 1.5] и [5, -1]. После генерации мы применяем линейное преобразование, чтобы ввести некоторую корреляцию между признаками и сделать задачу более сложной. Это приводит к 2D набору данных с тремя перекрывающимися классами, подходящим для демонстрации различий между мультиномиальной и one-vs-rest логистической регрессией.

import matplotlib.pyplot as plt
import numpy as np

from sklearn.datasets import make_blobs

centers = [[-5, 0], [0, 1.5], [5, -1]]
X, y = make_blobs(n_samples=1_000, centers=centers, random_state=40)
transformation = [[0.4, 0.2], [-0.4, 1.2]]
X = np.dot(X, transformation)

fig, ax = plt.subplots(figsize=(6, 4))

scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="black")
ax.set(title="Synthetic Dataset", xlabel="Feature 1", ylabel="Feature 2")
_ = ax.legend(*scatter.legend_elements(), title="Classes")

Обучение классификатора

Мы обучаем два разных классификатора логистической регрессии: мультиномиальный и one-vs-rest. Мультиномиальный классификатор обрабатывает все классы одновременно, в то время как подход one-vs-rest обучает бинарный классификатор для каждого класса против всех остальных.

from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier

logistic_regression_multinomial = LogisticRegression().fit(X, y)
logistic_regression_ovr = OneVsRestClassifier(LogisticRegression()).fit(X, y)

accuracy_multinomial = logistic_regression_multinomial.score(X, y)
accuracy_ovr = logistic_regression_ovr.score(X, y)

Визуализация границ решений

Давайте визуализируем границы решений обеих моделей, которые предоставляются методом predict классификаторов.

from sklearn.inspection import DecisionBoundaryDisplay

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)

for model, title, ax in [
    (
        logistic_regression_multinomial,
        f"Multinomial Logistic Regression\n(Accuracy: {accuracy_multinomial:.3f})",
        ax1,
    ),
    (
        logistic_regression_ovr,
        f"One-vs-Rest Logistic Regression\n(Accuracy: {accuracy_ovr:.3f})",
        ax2,
    ),
]:
    DecisionBoundaryDisplay.from_estimator(
        model,
        X,
        ax=ax,
        response_method="predict",
        alpha=0.8,
    )
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
    legend = ax.legend(*scatter.legend_elements(), title="Classes")
    ax.add_artist(legend)
    ax.set_title(title)

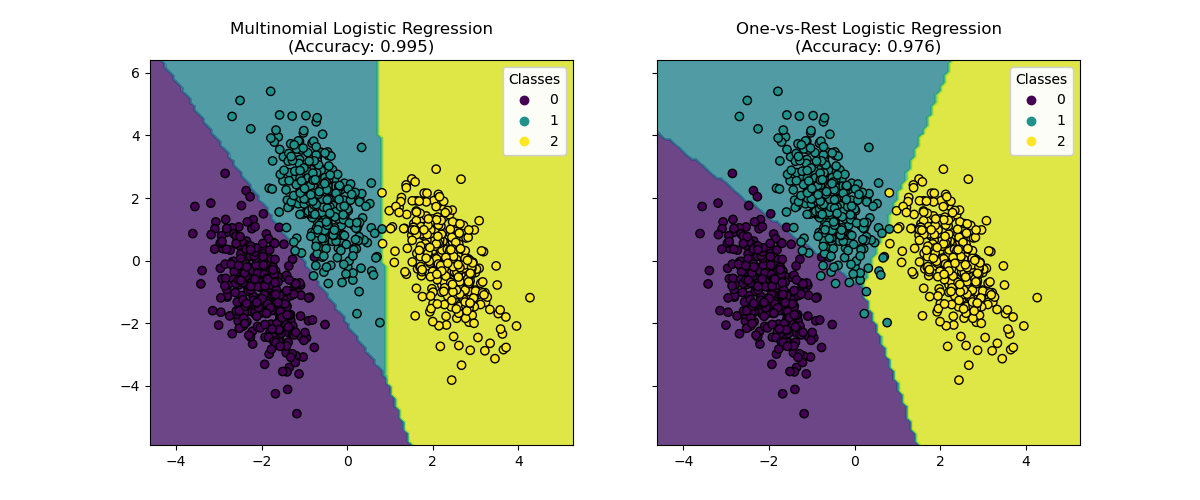
Мы видим, что границы решений различны. Это различие проистекает из их подходов:

• Мультиномиальная логистическая регрессия рассматривает все классы одновременно во время оптимизации.

• Логистическая регрессия «один против всех» обучает каждый класс независимо против всех остальных.

Эти различные стратегии могут приводить к разным границам принятия решений, особенно в сложных многоклассовых задачах.

Визуализация гиперплоскостей

Мы также визуализируем гиперплоскости, которые соответствуют линии, когда оценка вероятности для класса равна 0.5.

def plot_hyperplanes(classifier, X, ax):
    xmin, xmax = X[:, 0].min(), X[:, 0].max()
    ymin, ymax = X[:, 1].min(), X[:, 1].max()
    ax.set(xlim=(xmin, xmax), ylim=(ymin, ymax))

    if isinstance(classifier, OneVsRestClassifier):
        coef = np.concatenate([est.coef_ for est in classifier.estimators_])
        intercept = np.concatenate([est.intercept_ for est in classifier.estimators_])
    else:
        coef = classifier.coef_
        intercept = classifier.intercept_

    for i in range(coef.shape[0]):
        w = coef[i]
        a = -w[0] / w[1]
        xx = np.linspace(xmin, xmax)
        yy = a * xx - (intercept[i]) / w[1]
        ax.plot(xx, yy, "--", linewidth=3, label=f"Class {i}")

    return ax.get_legend_handles_labels()

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)

for model, title, ax in [
    (
        logistic_regression_multinomial,
        "Multinomial Logistic Regression Hyperplanes",
        ax1,
    ),
    (logistic_regression_ovr, "One-vs-Rest Logistic Regression Hyperplanes", ax2),
]:
    hyperplane_handles, hyperplane_labels = plot_hyperplanes(model, X, ax)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k")
    scatter_handles, scatter_labels = scatter.legend_elements()

    all_handles = hyperplane_handles + scatter_handles
    all_labels = hyperplane_labels + scatter_labels

    ax.legend(all_handles, all_labels, title="Classes")
    ax.set_title(title)

plt.show()

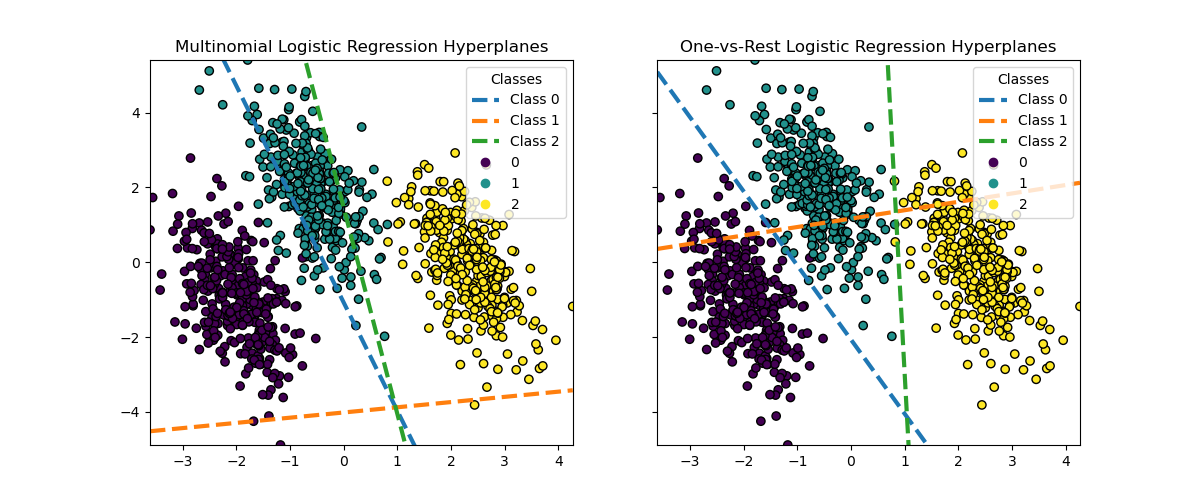
Хотя гиперплоскости для классов 0 и 2 довольно похожи между двумя методами, мы наблюдаем, что гиперплоскость для класса 1 заметно отличается. Это различие проистекает из фундаментальных подходов one-vs-rest и мультиномиальной логистической регрессии:

Для логистической регрессии "один против всех":

• Каждая гиперплоскость определяется независимо, рассматривая один класс против всех остальных.

• Для класса 1 гиперплоскость представляет границу решения, которая наилучшим образом разделяет класс 1 от объединенных классов 0 и 2.

• Такой бинарный подход может привести к более простым границам решений, но может не учитывать сложные взаимосвязи между всеми классами одновременно.

• Невозможно интерпретировать условные вероятности классов.

Для мультиномиальной логистической регрессии:

• Все гиперплоскости определяются одновременно, учитывая взаимосвязи между всеми классами сразу.

• Потери, минимизируемые моделью, являются правильным правилом оценки, что означает, что модель оптимизирована для оценки условных вероятностей классов, которые, следовательно, имеют смысл.

• Каждая гиперплоскость представляет границу принятия решения, где вероятность одного класса становится выше, чем у других, на основе общего распределения вероятностей.

• Этот подход может улавливать более тонкие взаимосвязи между классами, потенциально приводя к более точной классификации в многоклассовых задачах.

Различие в гиперплоскостях, особенно для класса 1, показывает, как эти методы могут создавать разные границы решений, несмотря на схожую общую точность.

На практике рекомендуется использовать мультиномиальную логистическую регрессию, поскольку она минимизирует хорошо сформулированную функцию потерь, что приводит к лучше калиброванным вероятностям классов и, следовательно, к более интерпретируемым результатам. Что касается границ решений, следует сформулировать функцию полезности для преобразования вероятностей классов в значимую величину для конкретной задачи. One-vs-rest позволяет использовать различные границы решений, но не обеспечивает детального контроля над компромиссом между классами, как это делает функция полезности.

Связанные примеры

Многоклассовая разреженная логистическая регрессия на 20newsgroups

Многоклассовая разреженная логистическая регрессия на 20newsgroups

Построить график вероятности классификации

Построить график вероятности классификации

Признаки ограниченной машины Больцмана для классификации цифр

Признаки ограниченной машины Больцмана для классификации цифр

Построение многоклассового SGD на наборе данных iris

Построение многоклассового SGD на наборе данных iris