Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Модели на основе L1 для разреженных сигналов#

Данный пример сравнивает три регрессионные модели на основе l1 на синтетическом сигнале, полученном из разреженных и коррелированных признаков, которые дополнительно искажены аддитивным гауссовым шумом:

a Lasso;
атрибут данного класса. Автоматическое определение релевантности - ARD;
атрибут данного класса. Elastic-Net.

Известно, что оценки Lasso становятся близкими к оценкам выбора модели при увеличении размерности данных, при условии, что нерелевантные переменные не слишком коррелированы с релевантными. При наличии коррелированных признаков Lasso сам по себе не может выбрать правильный паттерн разреженности [1].

Здесь мы сравниваем производительность трех моделей с точки зрения $R^2$ оценку, время обучения и разреженность оцененных коэффициентов по сравнению с истинными значениями.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

Сгенерировать синтетический набор данных#

Мы генерируем набор данных, где количество образцов меньше общего количества признаков. Это приводит к недоопределенной системе, т.е. решение не является уникальным, и поэтому мы не можем применить Метод наименьших квадратов само по себе. Регуляризация вводит штрафной член в целевую функцию, что изменяет задачу оптимизации и может помочь смягчить недоопределенный характер системы.

Целевая переменная y является линейной комбинацией с чередующимися знаками синусоидальных сигналов. Только 10 самых низких из 100 частот в X используются для генерации y, в то время как остальные признаки неинформативны. Это приводит к высокоразмерному разреженному пространству признаков, где необходима некоторая степень l1-регуляризации.

import numpy as np

rng = np.random.RandomState(0)
n_samples, n_features, n_informative = 50, 100, 10
time_step = np.linspace(-2, 2, n_samples)
freqs = 2 * np.pi * np.sort(rng.rand(n_features)) / 0.01
X = np.zeros((n_samples, n_features))

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step)

idx = np.arange(n_features)
true_coef = (-1) ** idx * np.exp(-idx / 10)
true_coef[n_informative:] = 0  # sparsify coef
y = np.dot(X, true_coef)

Некоторые из информативных признаков имеют близкие частоты для создания (анти-)корреляций.

freqs[:n_informative]

array([ 2.9502547 , 11.8059798 , 12.63394388, 12.70359377, 24.62241605,
       37.84077985, 40.30506066, 44.63327171, 54.74495357, 59.02456369])

Случайная фаза вводится с помощью numpy.random.random_sample и некоторый гауссов шум (реализованный через numpy.random.normal) добавляется как к признакам, так и к целевой переменной.

for i in range(n_features):
    X[:, i] = np.sin(freqs[i] * time_step + 2 * (rng.random_sample() - 0.5))
    X[:, i] += 0.2 * rng.normal(0, 1, n_samples)

y += 0.2 * rng.normal(0, 1, n_samples)

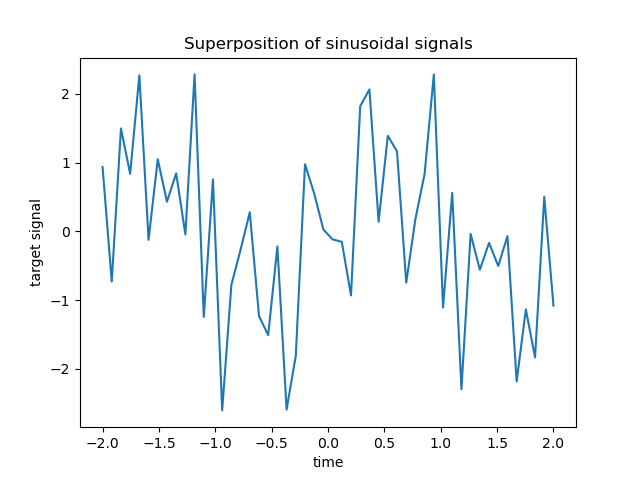
Такие разреженные, зашумлённые и коррелированные признаки могут быть получены, например, от сенсорных узлов, отслеживающих некоторые переменные окружающей среды, так как они обычно регистрируют схожие значения в зависимости от их расположения (пространственные корреляции). Мы можем визуализировать целевую переменную.

import matplotlib.pyplot as plt

plt.plot(time_step, y)
plt.ylabel("target signal")
plt.xlabel("time")
_ = plt.title("Superposition of sinusoidal signals")

Мы разделяем данные на обучающую и тестовую выборки для простоты. На практике следует использовать TimeSeriesSplit кросс-валидацию для оценки дисперсии тестовой оценки. Здесь мы устанавливаем shuffle="False" поскольку мы не должны использовать обучающие данные, которые следуют за тестовыми данными при работе с данными, имеющими временную зависимость.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, shuffle=False)

Далее мы вычисляем производительность трех моделей на основе l1 с точки зрения качества соответствия $R^2$ оценку и время обучения. Затем мы строим график, чтобы сравнить разреженность оцененных коэффициентов с истинными коэффициентами, и, наконец, анализируем предыдущие результаты.

Lasso#

В этом примере мы демонстрируем Lasso с фиксированным значением параметра регуляризации alphaНа практике оптимальный параметр alpha должен быть выбран путём передачи TimeSeriesSplit стратегию перекрестной проверки к LassoCV. Чтобы пример был простым и быстрым для выполнения, мы напрямую устанавливаем оптимальное значение для alpha здесь.

from time import time

from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score

t0 = time()
lasso = Lasso(alpha=0.14).fit(X_train, y_train)
print(f"Lasso fit done in {(time() - t0):.3f}s")

y_pred_lasso = lasso.predict(X_test)
r2_score_lasso = r2_score(y_test, y_pred_lasso)
print(f"Lasso r^2 on test data : {r2_score_lasso:.3f}")

Lasso fit done in 0.001s
Lasso r^2 on test data : 0.480

Автоматическое определение релевантности (ARD)#

Регрессия ARD — это байесовская версия Lasso. Она может производить интервальные оценки для всех параметров, включая дисперсию ошибки, если требуется. Это подходящий вариант, когда сигналы имеют гауссовский шум. См. пример Сравнение линейных байесовских регрессоров для сравнения ARDRegression и BayesianRidge регрессоры.

from sklearn.linear_model import ARDRegression

t0 = time()
ard = ARDRegression().fit(X_train, y_train)
print(f"ARD fit done in {(time() - t0):.3f}s")

y_pred_ard = ard.predict(X_test)
r2_score_ard = r2_score(y_test, y_pred_ard)
print(f"ARD r^2 on test data : {r2_score_ard:.3f}")

ARD fit done in 0.042s
ARD r^2 on test data : 0.543

ElasticNet#

ElasticNet является компромиссом между Lasso и Ridge, так как оно сочетает штраф L1 и L2. Количество регуляризации контролируется двумя гиперпараметрами l1_ratio и alpha. Для l1_ratio = 0 штраф является чистым L2, и модель эквивалентна Ridge. Аналогично, l1_ratio = 1 является чистой L1-штрафной функцией, и модель эквивалентна Lasso. Для 0 < l1_ratio < 1, штраф представляет собой комбинацию L1 и L2.

Как и ранее, мы обучаем модель с фиксированными значениями для alpha и l1_ratio. Для выбора их оптимального значения мы использовали ElasticNetCV, не показано здесь, чтобы сохранить пример простым.

from sklearn.linear_model import ElasticNet

t0 = time()
enet = ElasticNet(alpha=0.08, l1_ratio=0.5).fit(X_train, y_train)
print(f"ElasticNet fit done in {(time() - t0):.3f}s")

y_pred_enet = enet.predict(X_test)
r2_score_enet = r2_score(y_test, y_pred_enet)
print(f"ElasticNet r^2 on test data : {r2_score_enet:.3f}")

ElasticNet fit done in 0.001s
ElasticNet r^2 on test data : 0.636

Построение графика и анализ результатов#

В этом разделе мы используем тепловую карту для визуализации разреженности истинных и оцененных коэффициентов соответствующих линейных моделей.

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from matplotlib.colors import SymLogNorm

df = pd.DataFrame(
    {
        "True coefficients": true_coef,
        "Lasso": lasso.coef_,
        "ARDRegression": ard.coef_,
        "ElasticNet": enet.coef_,
    }
)

plt.figure(figsize=(10, 6))
ax = sns.heatmap(
    df.T,
    norm=SymLogNorm(linthresh=10e-4, vmin=-1, vmax=1),
    cbar_kws={"label": "coefficients' values"},
    cmap="seismic_r",
)
plt.ylabel("linear model")
plt.xlabel("coefficients")
plt.title(
    f"Models' coefficients\nLasso $R^2$: {r2_score_lasso:.3f}, "
    f"ARD $R^2$: {r2_score_ard:.3f}, "
    f"ElasticNet $R^2$: {r2_score_enet:.3f}"
)
plt.tight_layout()

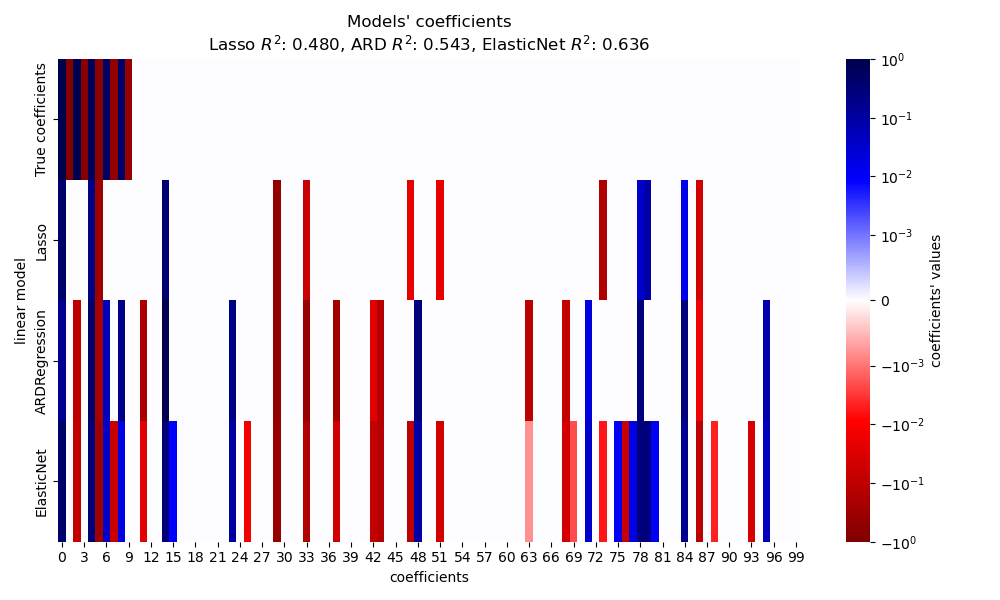
Models' coefficients Lasso $R^2$: 0.480, ARD $R^2$: 0.543, ElasticNet $R^2$: 0.636

В данном примере ElasticNet дает лучший результат и захватывает большинство прогностических признаков, но всё же не справляется с нахождением всех истинных компонентов. Обратите внимание, что оба ElasticNet и ARDRegression приведет к менее разреженной модели, чем Lasso.

Выводы#

Lasso известен эффективным восстановлением разреженных данных, но плохо работает с сильно коррелированными признаками. Действительно, если несколько коррелированных признаков вносят вклад в цель, Lasso в итоге выберет только один из них. В случае разреженных, но некоррелированных признаков, Lasso модель была бы более подходящей.

ElasticNet вводит некоторую разреженность в коэффициенты и сжимает их значения до нуля. Таким образом, при наличии коррелированных признаков, которые влияют на целевую переменную, модель всё ещё может уменьшить их веса, не устанавливая их точно в ноль. Это приводит к менее разреженной модели, чем чистая Lasso и может учитывать непредсказательные признаки.

ARDRegression лучше справляется с гауссовым шумом, но все еще не может обрабатывать коррелированные признаки и требует большего количества времени из-за подбора априорного распределения.

Ссылки#

Общее время выполнения скрипта: (0 минут 0.395 секунд)

Связанные примеры

Lasso на плотных и разреженных данных

Пути Lasso, Lasso-LARS и Elastic Net

Совместный отбор признаков с многозадачным Lasso

Влияние регуляризации модели на ошибку обучения и тестирования

Галерея, созданная Sphinx-Gallery