Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Коэффициенты Ridge как функция L2-регуляризации#
Модель, которая переобучается, слишком хорошо изучает обучающие данные, захватывая как основные закономерности, так и шум в данных. Однако при применении к новым данным изученные взаимосвязи могут не сохраняться. Обычно мы обнаруживаем это, когда применяем наши обученные предсказания к тестовым данным и видим, что статистическая производительность значительно падает по сравнению с обучающими данными.
Один из способов преодолеть переобучение — регуляризация, которая может быть выполнена путём штрафования больших весов (коэффициентов) в линейных моделях, заставляя модель уменьшать все коэффициенты. Регуляризация снижает зависимость модели от конкретной информации, полученной из обучающих выборок.
Этот пример иллюстрирует, как L2-регуляризация в
Ridge регрессия влияет на производительность модели,
добавляя штрафной член к функции потерь, который увеличивается с коэффициентами
\(\beta\).
Регуляризованная функция потерь задаётся как: \(\mathcal{L}(X, y, \beta) = \| y - X \beta \|^{2}_{2} + \alpha \| \beta \|^{2}_{2}\)
где \(X\) это входные данные, \(y\) является целевой переменной, \(\beta\) является вектором коэффициентов, связанных с признаками, и \(\alpha\) является силой регуляризации.
Регуляризованная функция потерь направлена на балансировку между точным прогнозированием обучающего набора и предотвращением переобучения.
В этой регуляризованной потере левая часть (например, \(\|y - X\beta\|^{2}_{2}\)) измеряет квадрат разницы между фактической целевой переменной, \(y\), и предсказанные значения. Минимизация только этого члена может привести к переобучению, так как модель может стать слишком сложной и чувствительной к шуму в обучающих данных.
Для решения проблемы переобучения, регуляризация Ridge добавляет ограничение, называемое штрафным членом, (\(\alpha \| \beta\|^{2}_{2}\)) к функции потерь. Этот штрафной член представляет собой сумму квадратов коэффициентов модели, умноженную на силу регуляризации \(\alpha\). Вводя это ограничение, регуляризация Ridge препятствует тому, чтобы любой отдельный коэффициент \(\beta_{i}\) от принятия чрезмерно большого значения и способствует меньшим и более равномерно распределенным коэффициентам. Более высокие значения \(\alpha\) принудительно направляет коэффициенты к нулю. Однако чрезмерно высокий \(\alpha\) может привести к недообученной модели, которая не улавливает важные закономерности в данных.
Таким образом, регуляризованная функция потерь объединяет член точности предсказания и член штрафа. Регулируя силу регуляризации, практики могут точно настроить степень ограничения, наложенного на веса, обучая модель, способную хорошо обобщаться на невидимые данные, избегая переобучения.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Цель этого примера#
Для демонстрации работы регуляризации Ridge мы создадим не зашумленный набор данных. Затем мы обучим регуляризованную модель на диапазоне значений силы регуляризации (\(\alpha\)) и построить, как обученные коэффициенты и среднеквадратичная ошибка между ними и исходными значениями ведут себя как функции силы регуляризации.
Создание нешумного набора данных#
Мы создаем игрушечный набор данных со 100 образцами и 10 признаками, подходящий для обнаружения регрессии. Из 10 признаков 8 являются информативными и вносят вклад в регрессию, в то время как оставшиеся 2 признака не оказывают никакого влияния на целевую переменную (их истинные коэффициенты равны 0). Обратите внимание, что в этом примере данные не содержат шума, поэтому мы можем ожидать, что наша модель регрессии точно восстановит истинные коэффициенты w.
from sklearn.datasets import make_regression
X, y, w = make_regression(
n_samples=100, n_features=10, n_informative=8, coef=True, random_state=1
)
# Obtain the true coefficients
print(f"The true coefficient of this regression problem are:\n{w}")
The true coefficient of this regression problem are:
[38.32634568 88.49665188 0. 29.75747153 0. 19.08699432
25.44381023 38.69892343 49.28808734 71.75949622]
Обучение Ridge Regressor#
Мы используем Ridge, линейная модель с L2-регуляризацией. Мы обучаем несколько моделей, каждая с разным значением параметра модели alpha, который является положительной константой, умножающей
член штрафа, контролируя силу регуляризации. Для каждой обученной модели
мы затем вычисляем ошибку между истинными коэффициентами w и коэффициенты, найденные моделью clf. Мы сохраняем идентифицированные коэффициенты
и вычисленные ошибки для соответствующих коэффициентов в списках, что
удобно для построения графиков.
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
clf = Ridge()
# Generate values for `alpha` that are evenly distributed on a logarithmic scale
alphas = np.logspace(-3, 4, 200)
coefs = []
errors_coefs = []
# Train the model with different regularisation strengths
for a in alphas:
clf.set_params(alpha=a).fit(X, y)
coefs.append(clf.coef_)
errors_coefs.append(mean_squared_error(clf.coef_, w))
Построение графиков обученных коэффициентов и среднеквадратических ошибок#
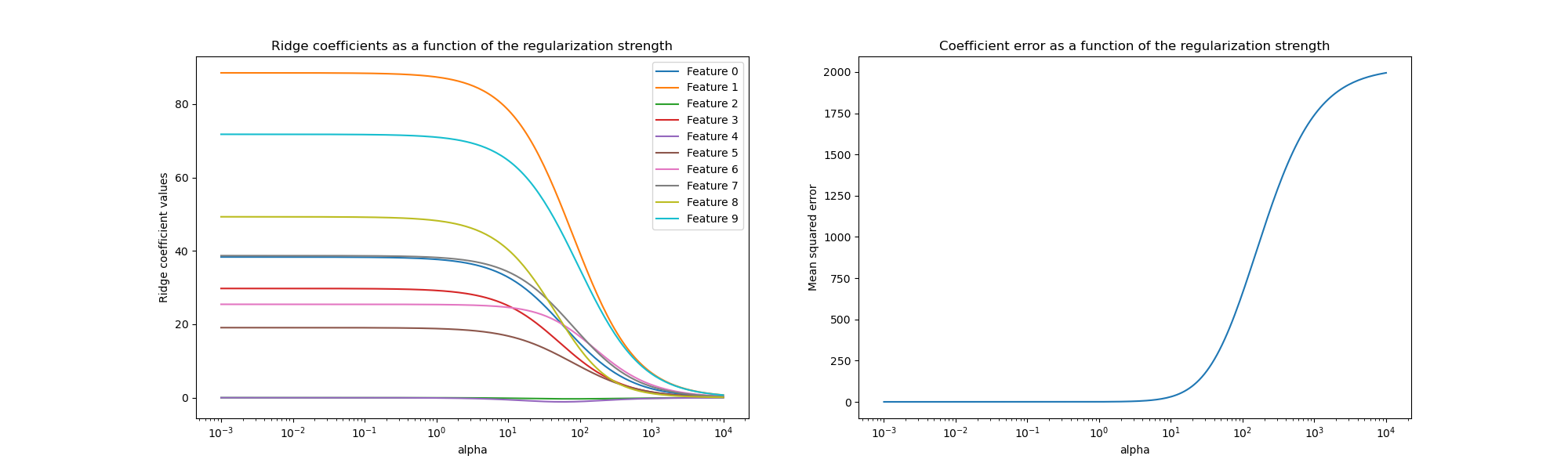
Теперь мы строим 10 различных регуляризованных коэффициентов как функцию
параметра регуляризации alpha где каждый цвет представляет различный
коэффициент.
Справа мы строим график того, как ошибки коэффициентов от оценщика меняются в зависимости от регуляризации.
import matplotlib.pyplot as plt
import pandas as pd
alphas = pd.Index(alphas, name="alpha")
coefs = pd.DataFrame(coefs, index=alphas, columns=[f"Feature {i}" for i in range(10)])
errors = pd.Series(errors_coefs, index=alphas, name="Mean squared error")
fig, axs = plt.subplots(1, 2, figsize=(20, 6))
coefs.plot(
ax=axs[0],
logx=True,
title="Ridge coefficients as a function of the regularization strength",
)
axs[0].set_ylabel("Ridge coefficient values")
errors.plot(
ax=axs[1],
logx=True,
title="Coefficient error as a function of the regularization strength",
)
_ = axs[1].set_ylabel("Mean squared error")
Интерпретация графиков#
График слева показывает, как сила регуляризации (alpha) влияет на коэффициенты регрессии Ridge. Меньшие значения alpha (слабая регуляризация), позволяют коэффициентам близко напоминать истинные коэффициенты (w), используемая для генерации набора данных. Это связано с тем, что
в наш искусственный набор данных не было добавлено дополнительного шума. Как alpha увеличивается, коэффициенты сжимаются к нулю, постепенно уменьшая влияние признаков, которые ранее были более значимыми.
График справа показывает среднеквадратичную ошибку (MSE) между
коэффициентами, найденными моделью, и истинными коэффициентами (w). Он предоставляет
меру, которая связана с тем, насколько точна наша гребневая модель по сравнению с истинной
порождающей моделью. Низкая ошибка означает, что она нашла коэффициенты ближе к
коэффициентам истинной порождающей модели. В этом случае, поскольку наш игрушечный набор данных был
незашумленным, мы видим, что наименее регуляризованная модель извлекает коэффициенты,
наиболее близкие к истинным коэффициентам (w) (ошибка близка к 0).
Когда alpha мал, модель захватывает тонкие детали
обучающих данных, вызванные ли шумом или фактической информацией. По мере того как
alpha увеличивается, самые высокие коэффициенты сжимаются быстрее, делая соответствующие признаки менее влиятельными в процессе обучения. Это может улучшить способность модели обобщать на невидимые данные (если было много шума для захвата), но также создает риск потери производительности, если регуляризация становится слишком сильной по сравнению с количеством шума в данных (как в этом примере).
В реальных сценариях, где данные обычно включают шум, выбор подходящего alpha значение становится критически важным для достижения баланса между переобученной и недообученной моделью.
Здесь мы увидели, что Ridge добавляет штраф к
коэффициентам для борьбы с переобучением. Другая проблема связана с
наличием выбросов в обучающем наборе данных. Выброс — это точка данных,
которая значительно отличается от других наблюдений. Конкретно, эти выбросы
влияют на левую часть функции потерь, которую мы показали ранее.
Некоторые другие линейные модели сформулированы так, чтобы быть устойчивыми к выбросам, такие как
HuberRegressor. Вы можете узнать больше об этом в HuberRegressor против Ridge на наборе данных с сильными выбросами пример.
Общее время выполнения скрипта: (0 минут 0.623 секунды)
Связанные примеры
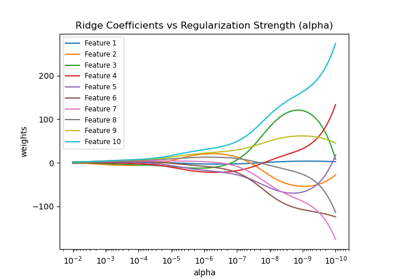
Построение коэффициентов Ridge как функции регуляризации

Влияние регуляризации модели на ошибку обучения и тестирования

Распространённые ошибки в интерпретации коэффициентов линейных моделей