Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Выбор модели Lasso: AIC-BIC / перекрёстная проверка#
Этот пример посвящён выбору модели для Lasso-моделей, которые являются линейными моделями с L1-штрафом для задач регрессии.
Действительно, можно использовать несколько стратегий для выбора значения параметра регуляризации: с помощью перекрестной проверки или с использованием информационного критерия, а именно AIC или BIC.
В дальнейшем мы подробно обсудим различные стратегии.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Набор данных#
В этом примере мы будем использовать набор данных по диабету.
from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True, as_frame=True)
X.head()
Кроме того, мы добавляем некоторые случайные признаки к исходным данным, чтобы лучше проиллюстрировать отбор признаков, выполняемый моделью Lasso.
import numpy as np
import pandas as pd
rng = np.random.RandomState(42)
n_random_features = 14
X_random = pd.DataFrame(
rng.randn(X.shape[0], n_random_features),
columns=[f"random_{i:02d}" for i in range(n_random_features)],
)
X = pd.concat([X, X_random], axis=1)
# Show only a subset of the columns
X[X.columns[::3]].head()
Выбор Lasso с помощью информационного критерия#
LassoLarsIC предоставляет оценщик Lasso, который
использует информационный критерий Акаике (AIC) или байесовский информационный
критерий (BIC) для выбора оптимального значения параметра
регуляризации alpha.
Перед обучением модели мы стандартизируем данные с помощью
StandardScaler. Кроме того, мы измерим время подгонки и настройки гиперпараметра alpha, чтобы сравнить со стратегией перекрестной проверки.
Сначала мы обучим модель Lasso с критерием AIC.
import time
from sklearn.linear_model import LassoLarsIC
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
start_time = time.time()
lasso_lars_ic = make_pipeline(StandardScaler(), LassoLarsIC(criterion="aic")).fit(X, y)
fit_time = time.time() - start_time
Мы сохраняем метрику AIC для каждого значения alpha, использованного во время fit.
results = pd.DataFrame(
{
"alphas": lasso_lars_ic[-1].alphas_,
"AIC criterion": lasso_lars_ic[-1].criterion_,
}
).set_index("alphas")
alpha_aic = lasso_lars_ic[-1].alpha_
Теперь мы выполняем тот же анализ, используя критерий BIC.
lasso_lars_ic.set_params(lassolarsic__criterion="bic").fit(X, y)
results["BIC criterion"] = lasso_lars_ic[-1].criterion_
alpha_bic = lasso_lars_ic[-1].alpha_
Мы можем проверить, какое значение alpha приводит к минимальным значениям AIC и BIC.
def highlight_min(x):
x_min = x.min()
return ["font-weight: bold" if v == x_min else "" for v in x]
results.style.apply(highlight_min)
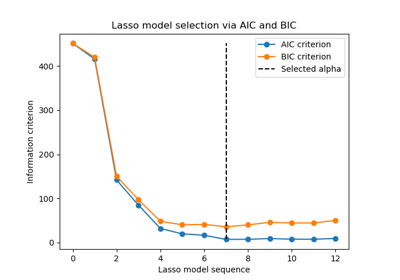
Наконец, мы можем построить значения AIC и BIC для различных значений альфа. Вертикальные линии на графике соответствуют альфа, выбранным для каждого критерия. Выбранное альфа соответствует минимуму критерия AIC или BIC.
ax = results.plot()
ax.vlines(
alpha_aic,
results["AIC criterion"].min(),
results["AIC criterion"].max(),
label="alpha: AIC estimate",
linestyles="--",
color="tab:blue",
)
ax.vlines(
alpha_bic,
results["BIC criterion"].min(),
results["BIC criterion"].max(),
label="alpha: BIC estimate",
linestyle="--",
color="tab:orange",
)
ax.set_xlabel(r"$\alpha$")
ax.set_ylabel("criterion")
ax.set_xscale("log")
ax.legend()
_ = ax.set_title(
f"Information-criterion for model selection (training time {fit_time:.2f}s)"
)
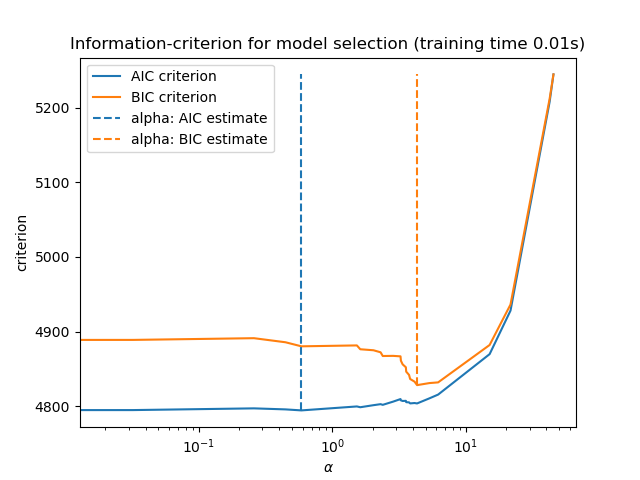
Выбор модели с информационным критерием очень быстр. Он основан на
вычислении критерия на внутривыборочном наборе, предоставленном fit. Оба критерия оценивают ошибку обобщения модели на основе ошибки обучающей выборки и штрафуют этот излишне оптимистичный результат. Однако этот штраф основан на правильной оценке степеней свободы и дисперсии шума. Оба выводятся для больших выборок (асимптотические результаты) и предполагают, что модель корректна, т.е. что данные фактически сгенерированы этой моделью.
Эти модели также имеют тенденцию ломаться, когда задача плохо обусловлена (больше признаков, чем образцов). Тогда требуется предоставить оценку дисперсии шума.
Выбор Lasso с помощью кросс-валидации#
Оценщик Lasso может быть реализован с разными решателями: координатный спуск и регрессия наименьшего угла. Они различаются по скорости выполнения и источникам численных ошибок.
В scikit-learn доступны два различных оценщика со встроенной перекрестной проверкой: LassoCV и
LassoLarsCV , которые соответственно решают проблему с координатным спуском и регрессией наименьшего угла.
В оставшейся части этого раздела мы представим оба подхода. Для обоих алгоритмов мы будем использовать стратегию 20-кратной перекрестной проверки.
Lasso через координатный спуск#
Начнём с настройки гиперпараметров с помощью
LassoCV.
from sklearn.linear_model import LassoCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
import matplotlib.pyplot as plt
ymin, ymax = 2300, 3800
lasso = model[-1]
plt.semilogx(lasso.alphas_, lasso.mse_path_, linestyle=":")
plt.plot(
lasso.alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha: CV estimate")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
_ = plt.title(
f"Mean square error on each fold: coordinate descent (train time: {fit_time:.2f}s)"
)
Lasso через регрессию наименьших углов#
Начнём с настройки гиперпараметров с помощью
LassoLarsCV.
from sklearn.linear_model import LassoLarsCV
start_time = time.time()
model = make_pipeline(StandardScaler(), LassoLarsCV(cv=20)).fit(X, y)
fit_time = time.time() - start_time
lasso = model[-1]
plt.semilogx(lasso.cv_alphas_, lasso.mse_path_, ":")
plt.semilogx(
lasso.cv_alphas_,
lasso.mse_path_.mean(axis=-1),
color="black",
label="Average across the folds",
linewidth=2,
)
plt.axvline(lasso.alpha_, linestyle="--", color="black", label="alpha CV")
plt.ylim(ymin, ymax)
plt.xlabel(r"$\alpha$")
plt.ylabel("Mean square error")
plt.legend()
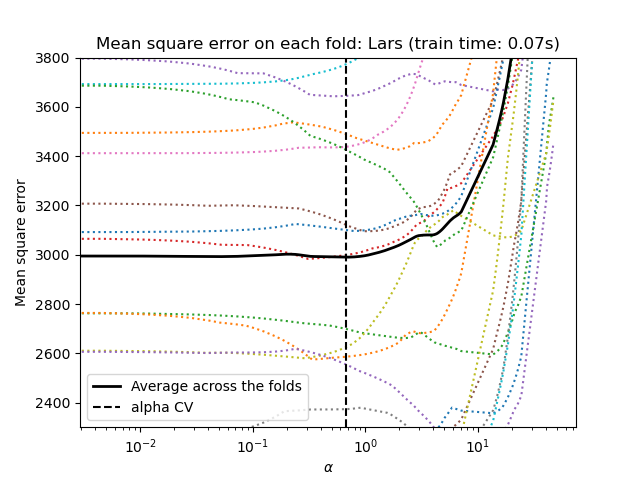
_ = plt.title(f"Mean square error on each fold: Lars (train time: {fit_time:.2f}s)")
Сводка подхода перекрестной проверки#
Оба алгоритма дают примерно одинаковые результаты.
Lars вычисляет путь решения только для каждого изгиба пути. В результате он очень эффективен, когда изгибов мало, что имеет место, если признаков или выборок немного. Также он может вычислить весь путь без установки каких-либо гиперпараметров. В отличие от этого, координатный спуск вычисляет точки пути на предварительно заданной сетке (здесь используется стандартная). Таким образом, он более эффективен, если количество точек сетки меньше, чем количество изгибов пути. Такая стратегия может быть интересна, если количество признаков действительно велико и достаточно выборок для выбора в каждом сгибе перекрестной проверки. С точки зрения численных ошибок, для сильно коррелированных переменных Lars будет накапливать больше ошибок, в то время как алгоритм координатного спуска будет только сэмплировать путь на сетке.
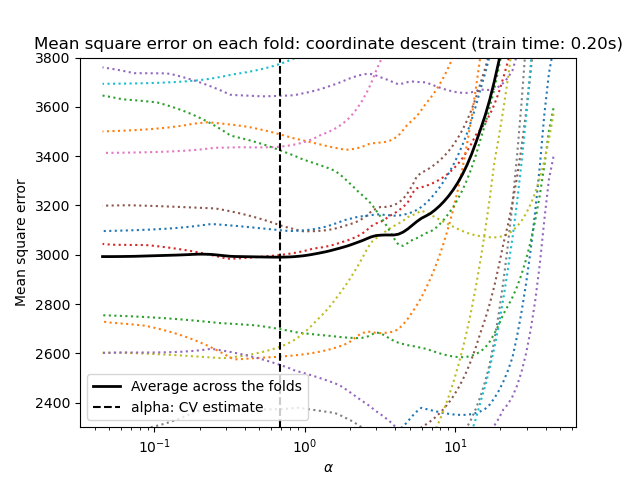
Обратите внимание, как оптимальное значение альфа варьируется для каждого фолда. Это иллюстрирует, почему вложенная кросс-валидация является хорошей стратегией при оценке производительности метода, для которого параметр выбирается с помощью кросс-валидации: этот выбор параметра может быть неоптимальным для окончательной оценки на невидимом тестовом наборе.
Заключение#
В этом руководстве мы представили два подхода для выбора лучшего гиперпараметра alpha: одна стратегия находит оптимальное значение alpha
используя только обучающий набор и некоторый информационный критерий, а другая стратегия основана на перекрёстной проверке.
В этом примере оба подхода работают схожим образом. Внутривыборочный выбор гиперпараметров даже демонстрирует свою эффективность с точки зрения вычислительной производительности. Однако его можно использовать только тогда, когда количество образцов достаточно велико по сравнению с количеством признаков.
Вот почему оптимизация гиперпараметров с помощью перекрестной проверки является безопасной стратегией: она работает в различных условиях.
Общее время выполнения скрипта: (0 минут 0.760 секунд)
Связанные примеры
Выбор модели Lasso с помощью информационных критериев