Распространённые ошибки в интерпретации коэффициентов линейных моделей

В линейных моделях целевое значение моделируется как линейная комбинация признаков (см. Линейные модели раздел Руководства пользователя для описания набора линейных моделей, доступных в scikit-learn). Коэффициенты в множественных линейных моделях представляют связь между данным признаком, \(X_i\) и целевая переменная, \(y\), предполагая, что все остальные признаки остаются постоянными (условная зависимость). Это отличается от построения \(X_i\) против \(y\) и подгонка линейной зависимости: в этом случае все возможные значения других признаков учитываются в оценке (маргинальная зависимость).

Этот пример даст некоторые подсказки по интерпретации коэффициентов в линейных моделях, указывая на проблемы, возникающие, когда либо линейная модель не подходит для описания набора данных, либо когда признаки коррелированы.

Примечание

Имейте в виду, что признаки \(X\) и результат \(y\) в целом являются результатом процесса генерации данных, который нам неизвестен. Модели машинного обучения обучаются для аппроксимации ненаблюдаемой математической функции, которая связывает \(X\) to \(y\) из выборочных данных. В результате любая интерпретация, сделанная о модели, не обязательно обобщается на истинный процесс генерации данных. Это особенно верно, когда модель низкого качества или когда выборочные данные не репрезентативны для генеральной совокупности.

Мы будем использовать данные из «Текущее обследование населения» с 1985 года для прогнозирования заработной платы как функции различных признаков, таких как опыт, возраст или образование.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns

Набор данных: заработная плата

Мы загружаем данные из OpenML. Обратите внимание, что установка параметра as_frame установка в True позволит получить данные в виде pandas dataframe.

from sklearn.datasets import fetch_openml

survey = fetch_openml(data_id=534, as_frame=True)

Затем мы идентифицируем признаки X и цель y: столбец WAGE является нашей целевой переменной (т.е. переменной, которую мы хотим предсказать).

X = survey.data[survey.feature_names]
X.describe(include="all")

	EDUCATION	SOUTH	SEX	ОПЫТ	UNION	AGE	RACE	OCCUPATION	SECTOR	MARR
count	534.000000	534	534	534.000000	534	534.000000	534	534	534	534
уникальный	NaN	2	2	NaN	2	NaN	3	6	3	2
верх	NaN	нет	мужской	NaN	not_member	NaN	White	Другие	Другие	Женат/Замужем
freq	NaN	378	289	NaN	438	NaN	440	156	411	350
mean	13.018727	NaN	NaN	17.822097	NaN	36.833333	NaN	NaN	NaN	NaN
std	2.615373	NaN	NaN	12.379710	NaN	11.726573	NaN	NaN	NaN	NaN
min	2.000000	NaN	NaN	0.000000	NaN	18.000000	NaN	NaN	NaN	NaN
25%	12.000000	NaN	NaN	8.000000	NaN	28.000000	NaN	NaN	NaN	NaN
50%	12.000000	NaN	NaN	15.000000	NaN	35.000000	NaN	NaN	NaN	NaN
75%	15.000000	NaN	NaN	26.000000	NaN	44.000000	NaN	NaN	NaN	NaN
max	18.000000	NaN	NaN	55.000000	NaN	64.000000	NaN	NaN	NaN	NaN

Обратите внимание, что набор данных содержит категориальные и числовые переменные. Нам нужно будет учесть это при предобработке набора данных в дальнейшем.

X.head()

	EDUCATION	SOUTH	SEX	ОПЫТ	UNION	AGE	RACE	OCCUPATION	SECTOR	MARR
0	8	нет	женский	21	not_member	35	Латиноамериканец	Другие	Производство	Женат/Замужем
1	9	нет	женский	42	not_member	57	White	Другие	Производство	Женат/Замужем
2	12	нет	мужской	1	not_member	19	White	Другие	Производство	Неженат/Незамужем
3	12	нет	мужской	4	not_member	22	White	Другие	Другие	Неженат/Незамужем
4	12	нет	мужской	17	not_member	35	White	Другие	Другие	Женат/Замужем

Наша цель для предсказания: заработная плата. Заработная плата описывается как число с плавающей точкой в долларах в час.

y = survey.target.values.ravel()
survey.target.head()

0    5.10
1    4.95
2    6.67
3    4.00
4    7.50
Name: WAGE, dtype: float64

Мы разделяем выборку на обучающий и тестовый наборы данных. Только обучающий набор данных будет использоваться в следующем исследовательском анализе. Это способ имитировать реальную ситуацию, когда прогнозы выполняются на неизвестной цели, и мы не хотим, чтобы наш анализ и решения были смещены знанием тестовых данных.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

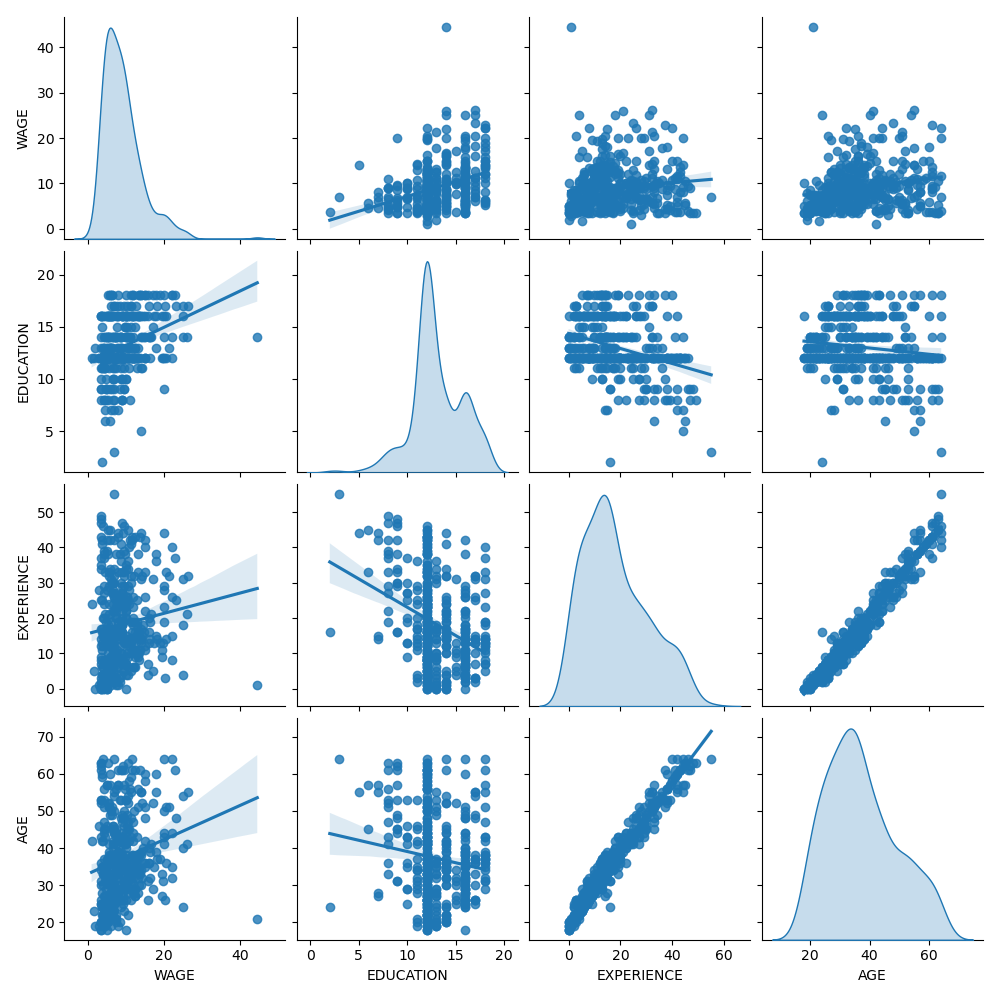
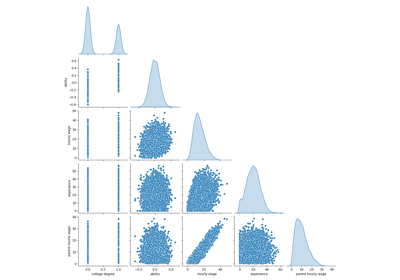
Сначала давайте получим некоторые представления, посмотрев на распределения переменных и на попарные отношения между ними. Будут использоваться только числовые переменные. На следующем графике каждая точка представляет образец.

train_dataset = X_train.copy()
train_dataset.insert(0, "WAGE", y_train)
_ = sns.pairplot(train_dataset, kind="reg", diag_kind="kde")

При внимательном рассмотрении распределения WAGE видно, что оно имеет длинный хвост. По этой причине мы должны взять его логарифм, чтобы приблизительно превратить его в нормальное распределение (линейные модели, такие как ридж или лассо, лучше всего работают для нормального распределения ошибок).

ЗАРПЛАТА увеличивается, когда ОБРАЗОВАНИЕ увеличивается. Обратите внимание, что зависимость между ЗАРПЛАТОЙ и ОБРАЗОВАНИЕМ, представленная здесь, является маргинальной зависимостью, т.е. она описывает поведение конкретной переменной без фиксации остальных.

Также, EXPERIENCE и AGE сильно линейно коррелированы.

Машинно-обучающий конвейер

Для проектирования нашего конвейера машинного обучения мы сначала вручную проверяем тип данных, с которыми работаем:

survey.data.info()

RangeIndex: 534 entries, 0 to 533
Data columns (total 10 columns):
 #   Column      Non-Null Count  Dtype
---  ------      --------------  -----
 0   EDUCATION   534 non-null    int64
 1   SOUTH       534 non-null    category
 2   SEX         534 non-null    category
 3   EXPERIENCE  534 non-null    int64
 4   UNION       534 non-null    category
 5   AGE         534 non-null    int64
 6   RACE        534 non-null    category
 7   OCCUPATION  534 non-null    category
 8   SECTOR      534 non-null    category
 9   MARR        534 non-null    category
dtypes: category(7), int64(3)
memory usage: 17.3 KB

Как было показано ранее, набор данных содержит столбцы с разными типами данных, и нам нужно применить специфическую предобработку для каждого типа данных. В частности, категориальные переменные не могут быть включены в линейную модель, если они не закодированы сначала как целые числа. Кроме того, чтобы избежать обработки категориальных признаков как упорядоченных значений, нам нужно применить one-hot-кодирование. Наш предобработчик будет:

• применить one-hot кодирование (т.е. создать столбец для каждой категории) к категориальным столбцам, только для небинарных категориальных переменных;

• в качестве первого подхода (мы увидим позже, как нормализация числовых значений повлияет на наше обсуждение), оставьте числовые значения как есть.

from sklearn.compose import make_column_transformer
from sklearn.preprocessing import OneHotEncoder

categorical_columns = ["RACE", "OCCUPATION", "SECTOR", "MARR", "UNION", "SEX", "SOUTH"]
numerical_columns = ["EDUCATION", "EXPERIENCE", "AGE"]

preprocessor = make_column_transformer(
    (OneHotEncoder(drop="if_binary"), categorical_columns),
    remainder="passthrough",
    verbose_feature_names_out=False,  # avoid to prepend the preprocessor names
)

Мы используем ридж-регрессор с очень маленькой регуляризацией для моделирования логарифма WAGE.

from sklearn.compose import TransformedTargetRegressor
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline

model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=Ridge(alpha=1e-10), func=np.log10, inverse_func=sp.special.exp10
    ),
)

Обработка набора данных

Сначала мы обучаем модель.

model.fit(X_train, y_train)

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(remainder='passthrough',
                                   transformers=[('onehotencoder',
                                                  OneHotEncoder(drop='if_binary'),
                                                  ['RACE', 'OCCUPATION',
                                                   'SECTOR', 'MARR', 'UNION',
                                                   'SEX', 'SOUTH'])],
                                   verbose_feature_names_out=False)),
                ('transformedtargetregressor',
                 TransformedTargetRegressor(func=,
                                            inverse_func=,
                                            regressor=Ridge(alpha=1e-10)))])

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Затем мы проверяем производительность вычисленной модели, строя график ее прогнозов против фактических значений на тестовом наборе и вычисляя медианную абсолютную ошибку.

from sklearn.metrics import PredictionErrorDisplay, median_absolute_error

mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
    "MedAE on training set": f"{mae_train:.2f} $/hour",
    "MedAE on testing set": f"{mae_test:.2f} $/hour",
}

_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
    y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, small regularization")
for name, score in scores.items():
    ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()

Модель, полученная в результате обучения, далека от хорошей модели, способной делать точные прогнозы: это очевидно при взгляде на график выше, где хорошие прогнозы должны лежать на черной пунктирной линии.

В следующем разделе мы интерпретируем коэффициенты модели. При этом мы должны помнить, что любые выводы, которые мы делаем, относятся к построенной нами модели, а не к истинному (реальному) процессу генерации данных.

Интерпретация коэффициентов: важность масштаба

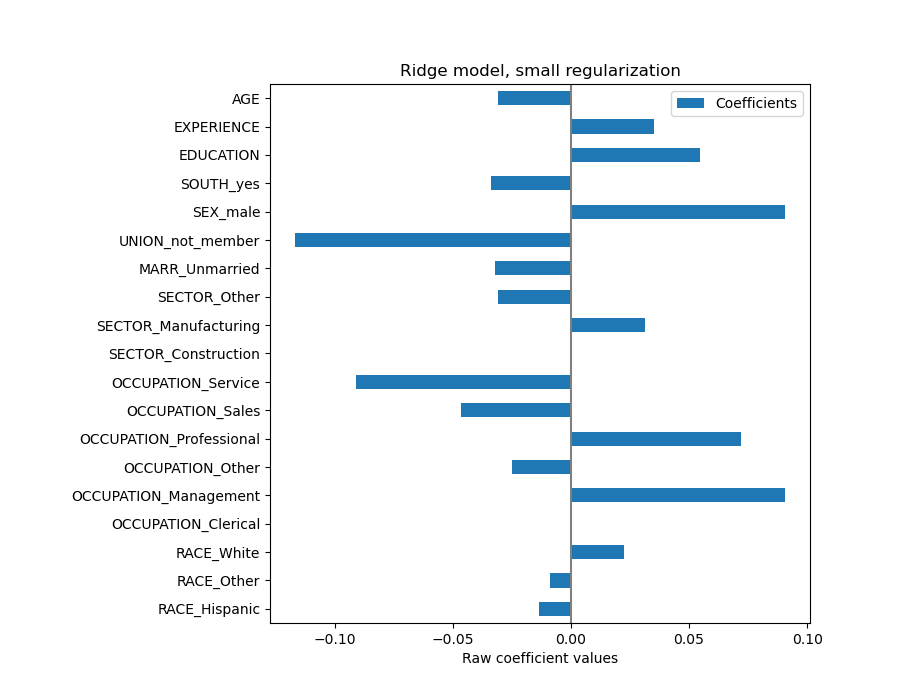
Прежде всего, мы можем взглянуть на значения коэффициентов подобранного нами регрессора.

feature_names = model[:-1].get_feature_names_out()

coefs = pd.DataFrame(
    model[-1].regressor_.coef_,
    columns=["Coefficients"],
    index=feature_names,
)

coefs

	Коэффициенты
RACE_Hispanic	-0.013520
РАСА_Другая	-0.009077
RACE_White	0.022593
OCCUPATION_Clerical	0.000045
OCCUPATION_Management	0.090528
OCCUPATION_Other	-0.025102
OCCUPATION_Professional	0.071964
OCCUPATION_Sales	-0.046636
OCCUPATION_Service	-0.091053
SECTOR_Construction	-0.000198
SECTOR_Manufacturing	0.031255
SECTOR_Other	-0.031026
MARR_Unmarried	-0.032405
UNION_not_member	-0.117154
SEX_male	0.090808
SOUTH_yes	-0.033823
EDUCATION	0.054699
ОПЫТ	0.035005
AGE	-0.030867

Коэффициент AGE выражен в "долларах/час за прожитые годы", а коэффициент EDUCATION — в "долларах/час за годы образования". Такое представление коэффициентов имеет преимущество в том, что делает ясными практические предсказания модели: увеличение \(1\) год в ВОЗРАСТЕ означает уменьшение на \(0.030867\) долларов/час, в то время как увеличение \(1\) год в EDUCATION означает увеличение \(0.054699\) долларов/час. С другой стороны, категориальные переменные (как UNION или SEX) — безразмерные числа, принимающие значение 0 или 1. Их коэффициенты выражены в долларах/час. Затем мы не можем сравнить величину разных коэффициентов, поскольку признаки имеют разные естественные масштабы и, следовательно, диапазоны значений из-за их разных единиц измерения. Это более заметно, если построить коэффициенты.

coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, small regularization")
plt.axvline(x=0, color=".5")
plt.xlabel("Raw coefficient values")
plt.subplots_adjust(left=0.3)

Действительно, из графика выше наиболее важным фактором в определении WAGE кажется переменная UNION, даже если наша интуиция может подсказывать, что переменные вроде EXPERIENCE должны иметь большее влияние.

Взгляд на график коэффициентов для оценки важности признаков может быть вводящим в заблуждение, поскольку некоторые из них варьируются в небольшом масштабе, в то время как другие, такие как AGE, варьируются гораздо больше, на несколько десятилетий.

Это видно, если сравнить стандартные отклонения разных признаков.

X_train_preprocessed = pd.DataFrame(
    model[:-1].transform(X_train), columns=feature_names
)

X_train_preprocessed.std(axis=0).plot.barh(figsize=(9, 7))
plt.title("Feature ranges")
plt.xlabel("Std. dev. of feature values")
plt.subplots_adjust(left=0.3)

Умножение коэффициентов на стандартное отклонение соответствующего признака привело бы все коэффициенты к одной единице измерения. Как мы увидим после это эквивалентно нормализации числовых переменных по их стандартному отклонению, как \(y = \sum{coef_i \times X_i} = \sum{(coef_i \times std_i) \times (X_i / std_i)}\).

Таким образом, мы подчеркиваем, что чем больше дисперсия признака, тем больше вес соответствующего коэффициента на выходе, при прочих равных условиях.

coefs = pd.DataFrame(
    model[-1].regressor_.coef_ * X_train_preprocessed.std(axis=0),
    columns=["Coefficient importance"],
    index=feature_names,
)
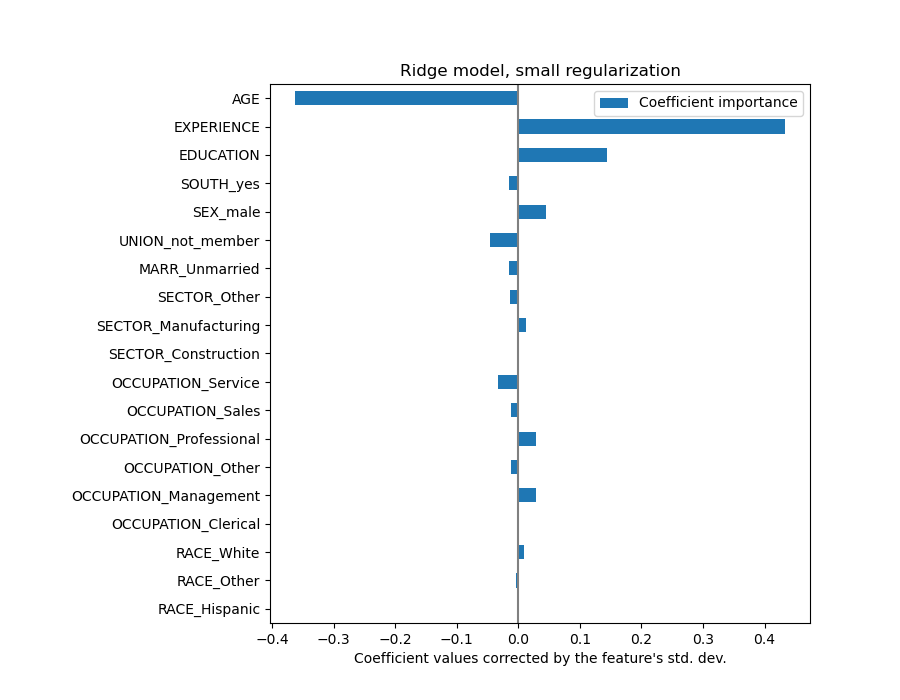
coefs.plot(kind="barh", figsize=(9, 7))
plt.xlabel("Coefficient values corrected by the feature's std. dev.")
plt.title("Ridge model, small regularization")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)

Теперь, когда коэффициенты масштабированы, их можно безопасно сравнивать.

Примечание

Почему график выше предполагает, что увеличение возраста приводит к уменьшению заработной платы? Почему начальный pairplot говоря противоположное? Это различие — разница между маргинальной и условной зависимостью.

Приведённый выше график показывает зависимости между конкретным признаком и целевой переменной, когда все остальные признаки остаются постоянными, т.е. условные зависимости. Увеличение AGE приведет к уменьшению WAGE при постоянстве всех других признаков. Напротив, увеличение EXPERIENCE приведет к увеличению WAGE при постоянстве всех других признаков. Также AGE, EXPERIENCE и EDUCATION — это три переменные, которые больше всего влияют на модель.

Интерпретация коэффициентов: осторожность в отношении причинности

Линейные модели — отличный инструмент для измерения статистической связи, но мы должны быть осторожны при утверждениях о причинно-следственной связи, ведь корреляция не всегда подразумевает причинность. Это особенно сложно в социальных науках, потому что наблюдаемые переменные служат лишь прокси для лежащего в основе причинного процесса.

В нашем конкретном случае мы можем рассматривать ОБРАЗОВАНИЕ человека как прокси для его профессиональной пригодности, реальной переменной, которая нас интересует, но которую мы не можем наблюдать. Мы, конечно, хотели бы думать, что более длительное пребывание в школе увеличивает техническую компетентность, но также вполне возможно, что причинность работает и в обратную сторону. То есть те, кто технически компетентен, как правило, дольше остаются в школе.

Работодатель вряд ли будет заботиться о том, какой это случай (или если это смесь обоих), пока он остаётся убеждённым, что человек с большим ОБРАЗОВАНИЕМ лучше подходит для работы, он будет готов платить более высокую ЗАРПЛАТУ.

Это смешение эффектов становится проблематичным при рассмотрении некоторых форм вмешательства, например, государственных субсидий на университетские степени или рекламных материалов, поощряющих людей получать высшее образование. Полезность этих мер может оказаться переоцененной, особенно если степень смешения сильна. Наша модель предсказывает \(0.054699\) увеличение почасовой оплаты за каждый год образования. Фактический причинный эффект может быть ниже из-за этого смешения.

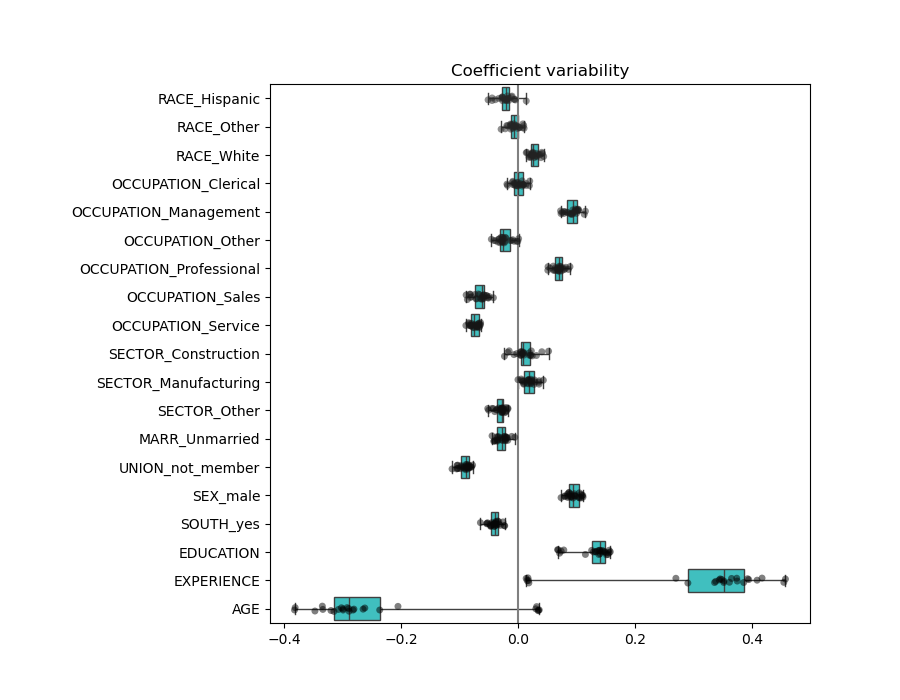
Проверка изменчивости коэффициентов

Мы можем проверить изменчивость коэффициентов с помощью перекрёстной проверки: это форма возмущения данных (связанная с ресемплинг).

Если коэффициенты значительно меняются при изменении входного набора данных, их устойчивость не гарантируется, и их, вероятно, следует интерпретировать с осторожностью.

from sklearn.model_selection import RepeatedKFold, cross_validate

cv = RepeatedKFold(n_splits=5, n_repeats=5, random_state=0)
cv_model = cross_validate(
    model,
    X,
    y,
    cv=cv,
    return_estimator=True,
    n_jobs=2,
)

coefs = pd.DataFrame(
    [
        est[-1].regressor_.coef_ * est[:-1].transform(X.iloc[train_idx]).std(axis=0)
        for est, (train_idx, _) in zip(cv_model["estimator"], cv.split(X, y))
    ],
    columns=feature_names,
)

plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=10)
plt.axvline(x=0, color=".5")
plt.xlabel("Coefficient importance")
plt.title("Coefficient importance and its variability")
plt.suptitle("Ridge model, small regularization")
plt.subplots_adjust(left=0.3)

Проблема коррелированных переменных

Коэффициенты AGE и EXPERIENCE подвержены сильной изменчивости, что может быть связано с коллинеарностью между двумя признаками: поскольку AGE и EXPERIENCE изменяются вместе в данных, их эффект трудно разделить.

Чтобы проверить эту интерпретацию, мы строим график изменчивости коэффициентов AGE и EXPERIENCE.

plt.xlabel("Age coefficient")
plt.ylabel("Experience coefficient")
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title("Co-variations of coefficients for AGE and EXPERIENCE across folds")

Две области заполнены: когда коэффициент EXPERIENCE положительный, коэффициент AGE отрицательный, и наоборот.

Чтобы продвинуться дальше, мы удаляем один из двух признаков, AGE, и проверяем, каково влияние на стабильность модели.

column_to_drop = ["AGE"]

cv_model = cross_validate(
    model,
    X.drop(columns=column_to_drop),
    y,
    cv=cv,
    return_estimator=True,
    n_jobs=2,
)

coefs = pd.DataFrame(
    [
        est[-1].regressor_.coef_
        * est[:-1].transform(X.drop(columns=column_to_drop).iloc[train_idx]).std(axis=0)
        for est, (train_idx, _) in zip(cv_model["estimator"], cv.split(X, y))
    ],
    columns=feature_names[:-1],
)

plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5)
plt.axvline(x=0, color=".5")
plt.title("Coefficient importance and its variability")
plt.xlabel("Coefficient importance")
plt.suptitle("Ridge model, small regularization, AGE dropped")
plt.subplots_adjust(left=0.3)

Оценка коэффициента EXPERIENCE теперь показывает значительно сниженную вариабельность. EXPERIENCE остается важным для всех моделей, обученных во время кросс-валидации.

Предобработка числовых переменных

Как сказано выше (см. «Машинно-обучающий конвейер”), мы также можем выбрать масштабирование числовых значений перед обучением модели. Это может быть полезно, когда мы применяем аналогичное количество регуляризации ко всем из них в гребневой регрессии. Препроцессор переопределяется для вычитания среднего и масштабирования переменных до единичной дисперсии.

from sklearn.preprocessing import StandardScaler

preprocessor = make_column_transformer(
    (OneHotEncoder(drop="if_binary"), categorical_columns),
    (StandardScaler(), numerical_columns),
)

Модель останется неизменной.

model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=Ridge(alpha=1e-10), func=np.log10, inverse_func=sp.special.exp10
    ),
)
model.fit(X_train, y_train)

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(transformers=[('onehotencoder',
                                                  OneHotEncoder(drop='if_binary'),
                                                  ['RACE', 'OCCUPATION',
                                                   'SECTOR', 'MARR', 'UNION',
                                                   'SEX', 'SOUTH']),
                                                 ('standardscaler',
                                                  StandardScaler(),
                                                  ['EDUCATION', 'EXPERIENCE',
                                                   'AGE'])])),
                ('transformedtargetregressor',
                 TransformedTargetRegressor(func=,
                                            inverse_func=,
                                            regressor=Ridge(alpha=1e-10)))])

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Снова проверяем производительность вычисленной модели, используя медианную абсолютную ошибку.

mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
    "MedAE on training set": f"{mae_train:.2f} $/hour",
    "MedAE on testing set": f"{mae_test:.2f} $/hour",
}

_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
    y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, small regularization")
for name, score in scores.items():
    ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()

Для анализа коэффициентов масштабирование не требуется на этот раз, потому что оно было выполнено на этапе предобработки.

coefs = pd.DataFrame(
    model[-1].regressor_.coef_,
    columns=["Coefficients importance"],
    index=feature_names,
)
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, small regularization, normalized variables")
plt.xlabel("Raw coefficient values")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)

Теперь мы исследуем коэффициенты по нескольким фолдам кросс-валидации.

cv_model = cross_validate(
    model,
    X,
    y,
    cv=cv,
    return_estimator=True,
    n_jobs=2,
)
coefs = pd.DataFrame(
    [est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)

plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=10)
plt.axvline(x=0, color=".5")
plt.title("Coefficient variability")
plt.subplots_adjust(left=0.3)

Результат довольно похож на случай без нормализации.

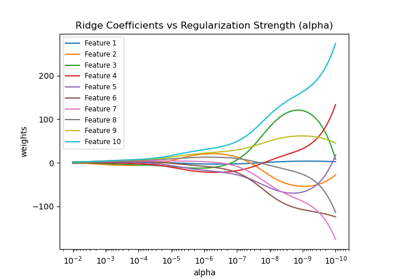
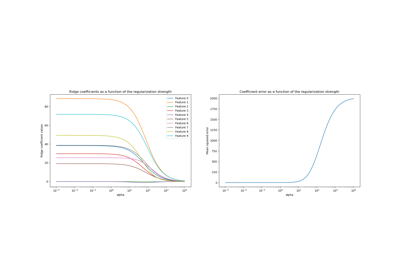
Линейные модели с регуляризацией

В практике машинного обучения гребневая регрессия чаще используется с непренебрежимо малым регуляризатором.

Выше мы ограничили это регуляризацию очень малым количеством. Регуляризация улучшает обусловленность задачи и уменьшает дисперсию оценок. RidgeCV применяет перекрестную проверку, чтобы определить, какое значение параметра регуляризации (alpha) лучше всего подходит для предсказания.

from sklearn.linear_model import RidgeCV

alphas = np.logspace(-10, 10, 21)  # alpha values to be chosen from by cross-validation
model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=RidgeCV(alphas=alphas),
        func=np.log10,
        inverse_func=sp.special.exp10,
    ),
)
model.fit(X_train, y_train)

Pipeline(steps=[('columntransformer',
                 ColumnTransformer(transformers=[('onehotencoder',
                                                  OneHotEncoder(drop='if_binary'),
                                                  ['RACE', 'OCCUPATION',
                                                   'SECTOR', 'MARR', 'UNION',
                                                   'SEX', 'SOUTH']),
                                                 ('standardscaler',
                                                  StandardScaler(),
                                                  ['EDUCATION', 'EXPERIENCE',
                                                   'AGE'])])),
                ('transformedtargetregressor',
                 TransformedTargetRegressor(func=,
                                            inverse_func=,
                                            regressor=RidgeCV(alphas=array([1.e-10, 1.e-09, 1.e-08, 1.e-07, 1.e-06, 1.e-05, 1.e-04, 1.e-03,
       1.e-02, 1.e-01, 1.e+00, 1.e+01, 1.e+02, 1.e+03, 1.e+04, 1.e+05,
       1.e+06, 1.e+07, 1.e+08, 1.e+09, 1.e+10]))))])

В среде Jupyter, пожалуйста, перезапустите эту ячейку, чтобы показать HTML-представление, или доверьтесь блокноту.
На GitHub HTML-представление не может отображаться, попробуйте загрузить эту страницу с помощью nbviewer.org.

Сначала мы проверяем, какое значение \(\alpha\) был выбран.

model[-1].regressor_.alpha_

10.0

Затем мы проверяем качество предсказаний.

mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
    "MedAE on training set": f"{mae_train:.2f} $/hour",
    "MedAE on testing set": f"{mae_test:.2f} $/hour",
}

_, ax = plt.subplots(figsize=(5, 5))
display = PredictionErrorDisplay.from_predictions(
    y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Ridge model, optimum regularization")
for name, score in scores.items():
    ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()

Способность воспроизводить данные регуляризованной модели аналогична таковой у нерегуляризованной модели.

coefs = pd.DataFrame(
    model[-1].regressor_.coef_,
    columns=["Coefficients importance"],
    index=feature_names,
)
coefs.plot.barh(figsize=(9, 7))
plt.title("Ridge model, with regularization, normalized variables")
plt.xlabel("Raw coefficient values")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)

Коэффициенты значительно различаются. Коэффициенты AGE и EXPERIENCE оба положительны, но теперь они оказывают меньшее влияние на прогноз.

Регуляризация уменьшает влияние коррелированных переменных на модель, потому что вес распределяется между двумя прогностическими переменными, поэтому ни одна из них в отдельности не будет иметь сильных весов.

С другой стороны, веса, полученные с регуляризацией, более устойчивы (см. Ридж-регрессия и классификация раздел руководства пользователя). Эта повышенная стабильность видна на графике, полученном из возмущений данных, в перекрёстной проверке. Этот график можно сравнить с предыдущий.

cv_model = cross_validate(
    model,
    X,
    y,
    cv=cv,
    return_estimator=True,
    n_jobs=2,
)
coefs = pd.DataFrame(
    [est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)

plt.xlabel("Age coefficient")
plt.ylabel("Experience coefficient")
plt.grid(True)
plt.xlim(-0.4, 0.5)
plt.ylim(-0.4, 0.5)
plt.scatter(coefs["AGE"], coefs["EXPERIENCE"])
_ = plt.title("Co-variations of coefficients for AGE and EXPERIENCE across folds")

Линейные модели с разреженными коэффициентами

Другая возможность учитывать коррелированные переменные в наборе данных — оценивать разреженные коэффициенты. В некотором смысле мы уже делали это вручную, когда удаляли столбец AGE в предыдущей оценке ridge.

Модели Lasso (см. Lasso раздел User Guide) оценивает разреженные коэффициенты. LassoCV применяет перекрёстную проверку для определения значения параметра регуляризации (alpha) лучше всего подходит для оценки модели.

from sklearn.linear_model import LassoCV

alphas = np.logspace(-10, 10, 21)  # alpha values to be chosen from by cross-validation
model = make_pipeline(
    preprocessor,
    TransformedTargetRegressor(
        regressor=LassoCV(alphas=alphas, max_iter=100_000),
        func=np.log10,
        inverse_func=sp.special.exp10,
    ),
)

_ = model.fit(X_train, y_train)

Сначала мы проверяем, какое значение \(\alpha\) был выбран.

model[-1].regressor_.alpha_

np.float64(0.001)

Затем мы проверяем качество предсказаний.

mae_train = median_absolute_error(y_train, model.predict(X_train))
y_pred = model.predict(X_test)
mae_test = median_absolute_error(y_test, y_pred)
scores = {
    "MedAE on training set": f"{mae_train:.2f} $/hour",
    "MedAE on testing set": f"{mae_test:.2f} $/hour",
}

_, ax = plt.subplots(figsize=(6, 6))
display = PredictionErrorDisplay.from_predictions(
    y_test, y_pred, kind="actual_vs_predicted", ax=ax, scatter_kwargs={"alpha": 0.5}
)
ax.set_title("Lasso model, optimum regularization")
for name, score in scores.items():
    ax.plot([], [], " ", label=f"{name}: {score}")
ax.legend(loc="upper left")
plt.tight_layout()

Для нашего набора данных модель снова не очень предсказуема.

coefs = pd.DataFrame(
    model[-1].regressor_.coef_,
    columns=["Coefficients importance"],
    index=feature_names,
)
coefs.plot(kind="barh", figsize=(9, 7))
plt.title("Lasso model, optimum regularization, normalized variables")
plt.axvline(x=0, color=".5")
plt.subplots_adjust(left=0.3)

Модель Lasso определяет корреляцию между AGE и EXPERIENCE и подавляет один из них для улучшения предсказания.

Важно помнить, что коэффициенты, которые были отброшены, могут все еще быть связаны с результатом сами по себе: модель выбрала их подавление, потому что они приносят мало или вообще не приносят дополнительной информации поверх других признаков. Кроме того, этот выбор нестабилен для коррелированных признаков и должен интерпретироваться с осторожностью.

Действительно, мы можем проверить изменчивость коэффициентов по фолдам.

cv_model = cross_validate(
    model,
    X,
    y,
    cv=cv,
    return_estimator=True,
    n_jobs=2,
)
coefs = pd.DataFrame(
    [est[-1].regressor_.coef_ for est in cv_model["estimator"]], columns=feature_names
)

plt.figure(figsize=(9, 7))
sns.stripplot(data=coefs, orient="h", palette="dark:k", alpha=0.5)
sns.boxplot(data=coefs, orient="h", color="cyan", saturation=0.5, whis=100)
plt.axvline(x=0, color=".5")
plt.title("Coefficient variability")
plt.subplots_adjust(left=0.3)

Мы наблюдаем, что коэффициенты AGE и EXPERIENCE сильно варьируются в зависимости от фолда.

Неправильная причинная интерпретация

Политики могут захотеть узнать влияние образования на заработную плату, чтобы оценить, имеет ли экономический смысл определенная политика, направленная на поощрение людей к получению большего образования. Хотя модели машинного обучения отлично подходят для измерения статистических связей, они, как правило, не способны выводить причинно-следственные эффекты.

Может возникнуть соблазн посмотреть на коэффициент образования в модели заработной платы из нашей последней модели (или любой другой модели) и сделать вывод, что он отражает истинный эффект изменения стандартизированной переменной образования на заработную плату.

К сожалению, вероятно существуют ненаблюдаемые смешивающие переменные, которые либо завышают, либо занижают этот коэффициент. Смешивающая переменная — это переменная, которая влияет как на EDUCATION, так и на WAGE. Одним из примеров такой переменной является способности. Предположительно, более способные люди с большей вероятностью получают образование, и в то же время с большей вероятностью зарабатывают более высокую почасовую оплату на любом уровне образования. В этом случае способности вызывают положительное Смещение из-за пропущенной переменной (OVB) на коэффициенте EDUCATION, тем самым преувеличивая влияние образования на заработную плату.

См. Неспособность машинного обучения выводить причинно-следственные связи для смоделированного случая способности OVB.

Извлеченные уроки

• Коэффициенты должны быть приведены к одной единице измерения для определения важности признаков. Масштабирование их с помощью стандартного отклонения признака является полезным приближением.

• Коэффициенты в многомерных линейных моделях представляют зависимость между данным признаком и целевой переменной, условный на других признаках.

• Коррелированные признаки вызывают нестабильность в коэффициентах линейных моделей, и их эффекты не могут быть хорошо разделены.

• Разные линейные модели по-разному реагируют на корреляцию признаков, и коэффициенты могут значительно отличаться друг от друга.

• Изучение коэффициентов по фолдам цикла перекрестной проверки дает представление об их стабильности.

• Интерпретация причинно-следственных связей затруднена при наличии смешивающих эффектов. Если связь между двумя переменными также подвержена влиянию чего-то ненаблюдаемого, следует быть осторожными при выводе заключений о причинности.

Связанные примеры

Коэффициенты Ridge как функция L2-регуляризации

Коэффициенты Ridge как функция L2-регуляризации

Неспособность машинного обучения выводить причинно-следственные связи

Неспособность машинного обучения выводить причинно-следственные связи

Построение коэффициентов Ridge как функции регуляризации

Построение коэффициентов Ridge как функции регуляризации

Влияние регуляризации модели на ошибку обучения и тестирования

Влияние регуляризации модели на ошибку обучения и тестирования