Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Регрессия Тейла-Сена#

Вычисляет регрессию Тейла-Сена на синтетическом наборе данных.

См. Оценщик Тейла-Сена: оценщик на основе обобщенной медианы Первые три столбца показывают прогнозируемую вероятность для различных значений двух признаков. Круглые маркеры представляют тестовые данные, которые были предсказаны как принадлежащие этому классу.

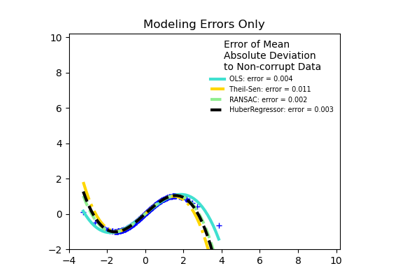
По сравнению с оценщиком OLS (обычный метод наименьших квадратов), оценщик Тейла-Сена устойчив к выбросам. Он имеет точку разрыва около 29,3% в случае простой линейной регрессии, что означает, что он может выдерживать произвольно искажённые данные (выбросы) до 29,3% в двумерном случае.

Оценка модели выполняется путём вычисления наклонов и свободных членов для подвыборки всех возможных комбинаций из p точек подвыборки. Если свободный член подгоняется, p должно быть больше или равно n_features + 1. Итоговый наклон и свободный член затем определяются как пространственная медиана этих наклонов и свободных членов.

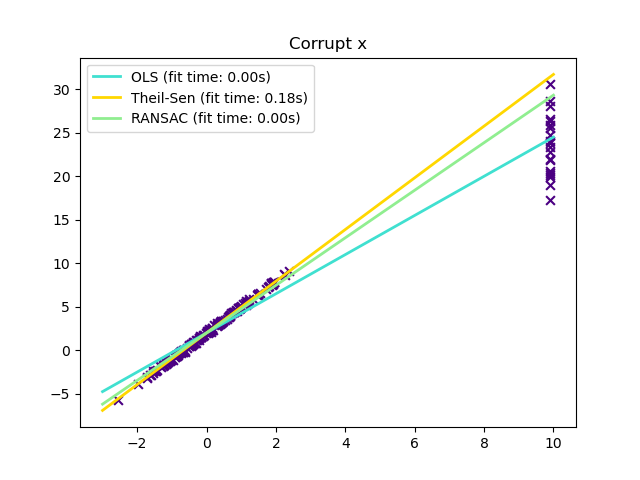
В некоторых случаях Theil-Sen работает лучше, чем RANSAC который также является устойчивым методом. Это проиллюстрировано во втором примере ниже, где выбросы по оси x нарушают работу RANSAC. Настройка residual_threshold параметр RANSAC исправляет это, но в целом необходимы априорные знания о данных и природе выбросов. Из-за вычислительной сложности Theil-Sen рекомендуется использовать его только для небольших задач по количеству выборок и признаков. Для больших задач max_subpopulation параметр ограничивает величину всех возможных комбинаций p точек подвыборки до случайно выбранного подмножества и, следовательно, также ограничивает время выполнения. Поэтому метод Тейла-Сена применим к более крупным задачам с недостатком потери некоторых математических свойств, поскольку он работает на случайном подмножестве.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np

from sklearn.linear_model import LinearRegression, RANSACRegressor, TheilSenRegressor

estimators = [
    ("OLS", LinearRegression()),
    ("Theil-Sen", TheilSenRegressor(random_state=42)),
    ("RANSAC", RANSACRegressor(random_state=42)),
]
colors = {"OLS": "turquoise", "Theil-Sen": "gold", "RANSAC": "lightgreen"}
lw = 2

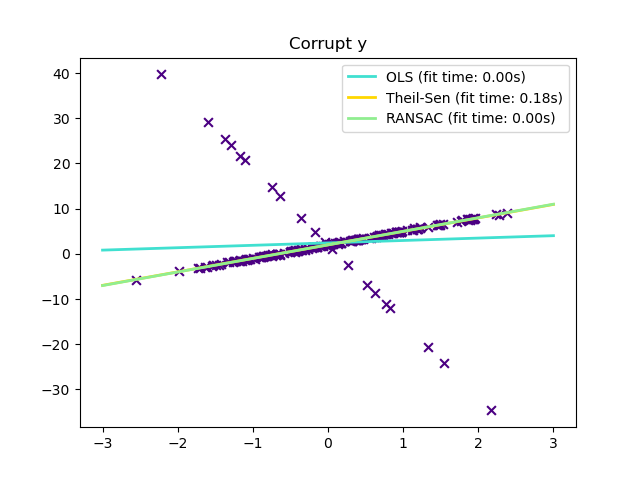
Выбросы только в направлении y#

np.random.seed(0)
n_samples = 200
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
w = 3.0
c = 2.0
noise = 0.1 * np.random.randn(n_samples)
y = w * x + c + noise
# 10% outliers
y[-20:] += -20 * x[-20:]
X = x[:, np.newaxis]

plt.scatter(x, y, color="indigo", marker="x", s=40)
line_x = np.array([-3, 3])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper right")
_ = plt.title("Corrupt y")

Выбросы в направлении X#

np.random.seed(0)
# Linear model y = 3*x + N(2, 0.1**2)
x = np.random.randn(n_samples)
noise = 0.1 * np.random.randn(n_samples)
y = 3 * x + 2 + noise
# 10% outliers
x[-20:] = 9.9
y[-20:] += 22
X = x[:, np.newaxis]

plt.figure()
plt.scatter(x, y, color="indigo", marker="x", s=40)

line_x = np.array([-3, 10])
for name, estimator in estimators:
    t0 = time.time()
    estimator.fit(X, y)
    elapsed_time = time.time() - t0
    y_pred = estimator.predict(line_x.reshape(2, 1))
    plt.plot(
        line_x,
        y_pred,
        color=colors[name],
        linewidth=lw,
        label="%s (fit time: %.2fs)" % (name, elapsed_time),
    )

plt.axis("tight")
plt.legend(loc="upper left")
plt.title("Corrupt x")
plt.show()