Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
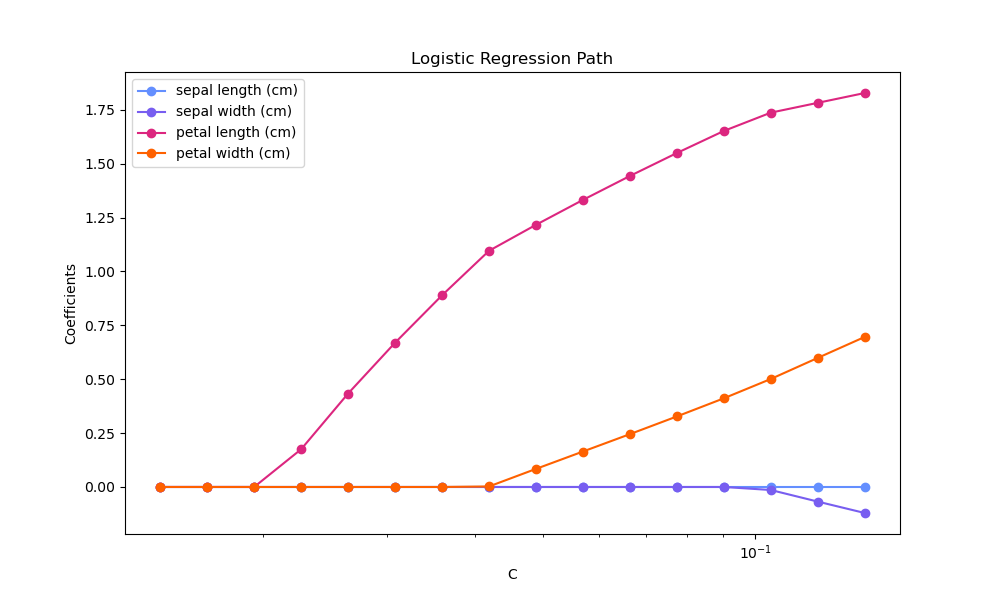
Регуляризационный путь L1-логистической регрессии#
Обучить логистические регрессии с l1-штрафом на задаче бинарной классификации, полученной из набора данных Iris.
Модели упорядочены от наиболее сильно регуляризованных к наименее регуляризованным. 4 коэффициента моделей собраны и построены как «путь регуляризации»: в левой части рисунка (сильные регуляризаторы) все коэффициенты точно равны 0. Когда регуляризация постепенно ослабляется, коэффициенты могут принимать ненулевые значения один за другим.
Здесь мы выбираем решатель liblinear, потому что он может эффективно оптимизировать функцию потерь логистической регрессии с негладким, индуцирующим разреженность штрафом l1.
Также обратите внимание, что мы установили низкое значение допуска, чтобы убедиться, что модель сошлась до сбора коэффициентов.
Мы также используем warm_start=True, что означает, что коэффициенты моделей используются повторно для инициализации следующей модели, чтобы ускорить вычисление полного пути.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Загрузка данных#
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
Здесь мы удаляем третий класс, чтобы сделать задачу бинарной классификацией
X = X[y != 2]
y = y[y != 2]
Вычислить путь регуляризации#
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import l1_min_c
cs = l1_min_c(X, y, loss="log") * np.logspace(0, 1, 16)
Создайте конвейер с StandardScaler и LogisticRegression, чтобы нормализовать
данные перед обучением линейной модели, чтобы ускорить сходимость и
сделать коэффициенты сопоставимыми. Кроме того, как побочный эффект, поскольку данные теперь
центрированы вокруг 0, нам не нужно подгонять свободный член.
clf = make_pipeline(
StandardScaler(),
LogisticRegression(
l1_ratio=1,
solver="liblinear",
tol=1e-6,
max_iter=int(1e6),
warm_start=True,
fit_intercept=False,
),
)
coefs_ = []
for c in cs:
clf.set_params(logisticregression__C=c)
clf.fit(X, y)
coefs_.append(clf["logisticregression"].coef_.ravel().copy())
coefs_ = np.array(coefs_)
Построить путь регуляризации#
import matplotlib.pyplot as plt
# Colorblind-friendly palette (IBM Color Blind Safe palette)
colors = ["#648FFF", "#785EF0", "#DC267F", "#FE6100"]
plt.figure(figsize=(10, 6))
for i in range(coefs_.shape[1]):
plt.semilogx(cs, coefs_[:, i], marker="o", color=colors[i], label=feature_names[i])
ymin, ymax = plt.ylim()
plt.xlabel("C")
plt.ylabel("Coefficients")
plt.title("Logistic Regression Path")
plt.legend()
plt.axis("tight")
plt.show()
Общее время выполнения скрипта: (0 минут 0.140 секунд)
Связанные примеры

Влияние регуляризации модели на ошибку обучения и тестирования
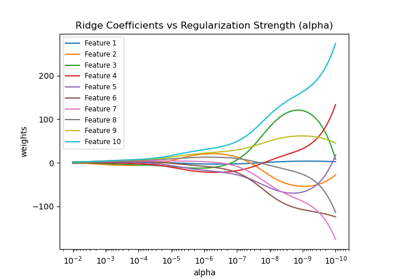
Построение коэффициентов Ridge как функции регуляризации
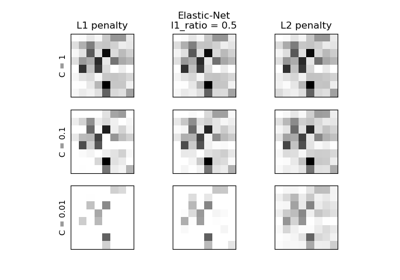
L1-штраф и разреженность в логистической регрессии