v_measure_score#
- sklearn.metrics.v_measure_score(labels_true, labels_pred, *, beta=1.0)[источник]#
V-мера кластеризации при заданной истинной разметке.
Эта оценка идентична
normalized_mutual_info_scoreс'arithmetic'опция для усреднения.V-мера - это гармоническое среднее между однородностью и полнотой:
v = (1 + beta) * homogeneity * completeness / (beta * homogeneity + completeness)
Эта метрика не зависит от абсолютных значений меток: перестановка значений меток классов или кластеров не изменит значение оценки никаким образом.
Эта метрика также симметрична: переключение
label_trueсlabel_predвернет то же значение оценки. Это может быть полезно для измерения согласованности двух независимых стратегий назначения меток на одном наборе данных, когда истинная основная истина неизвестна.Подробнее в Руководство пользователя.
- Параметры:
- labels_truearray-like формы (n_samples,)
Истинные метки классов, используемые в качестве эталона.
- labels_predarray-like формы (n_samples,)
Метки кластеров для оценки.
- betafloat, по умолчанию=1.0
Отношение веса, приписываемого
homogeneityпротивcompleteness. Еслиbetaбольше 1,completenessвзвешивается более сильно в расчете. Еслиbetaменьше 1,homogeneityвзвешивается сильнее.
- Возвращает:
- v_measurefloat
Оценка от 0.0 до 1.0. 1.0 означает идеально полную маркировку.
Смотрите также
homogeneity_scoreМетрика однородности кластерной разметки.
completeness_scoreМетрика полноты маркировки кластеров.
normalized_mutual_info_scoreНормализованная взаимная информация.
Ссылки
Примеры
Идеальные разметки одновременно однородны и полны, поэтому имеют оценку 1.0:
>>> from sklearn.metrics.cluster import v_measure_score >>> v_measure_score([0, 0, 1, 1], [0, 0, 1, 1]) 1.0 >>> v_measure_score([0, 0, 1, 1], [1, 1, 0, 0]) 1.0
Разметки, которые относят всех членов классов к одним и тем же кластерам, являются полными, но не однородными, поэтому штрафуются:
>>> print("%.6f" % v_measure_score([0, 0, 1, 2], [0, 0, 1, 1])) 0.8 >>> print("%.6f" % v_measure_score([0, 1, 2, 3], [0, 0, 1, 1])) 0.67
Разметки, имеющие чистые кластеры с элементами из одних и тех же классов, однородны, но ненужные разделения вредят полноте и, таким образом, также штрафуют V-меру:
>>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 0, 1, 2])) 0.8 >>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 1, 2, 3])) 0.67
Если элементы классов полностью разделены по разным кластерам, назначение полностью неполное, следовательно, V-мера равна нулю:
>>> print("%.6f" % v_measure_score([0, 0, 0, 0], [0, 1, 2, 3])) 0.0
Кластеры, включающие образцы из совершенно разных классов, полностью разрушают однородность маркировки, следовательно:
>>> print("%.6f" % v_measure_score([0, 0, 1, 1], [0, 0, 0, 0])) 0.0
Примеры галереи#

Бикластеризация документов с помощью алгоритма спектральной совместной кластеризации
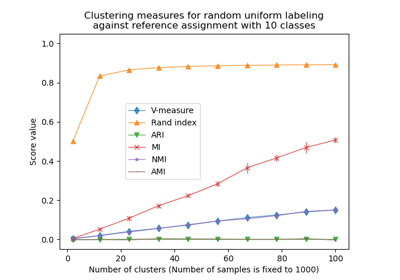
Коррекция на случайность в оценке производительности кластеризации
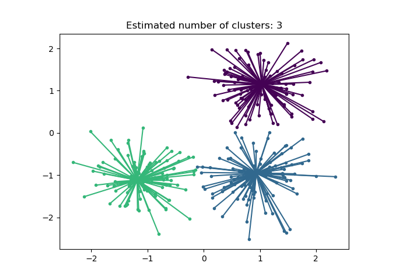
Демонстрация алгоритма кластеризации с распространением аффинности
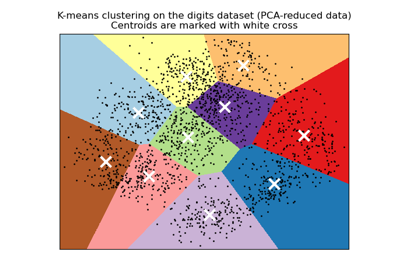
Демонстрация кластеризации K-Means на данных рукописных цифр
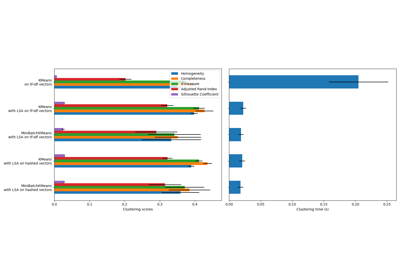
Кластеризация текстовых документов с использованием k-means