Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

Демонстрация алгоритма кластеризации HDBSCAN#

В этой демонстрации мы рассмотрим cluster.HDBSCAN с точки зрения обобщения cluster.DBSCAN алгоритм. Мы сравним оба алгоритма на конкретных наборах данных. Наконец, мы оценим чувствительность HDBSCAN к определенным гиперпараметрам.

Сначала определим пару вспомогательных функций для удобства.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import matplotlib.pyplot as plt
import numpy as np

from sklearn.cluster import DBSCAN, HDBSCAN
from sklearn.datasets import make_blobs


def plot(X, labels, probabilities=None, parameters=None, ground_truth=False, ax=None):
    if ax is None:
        _, ax = plt.subplots(figsize=(10, 4))
    labels = labels if labels is not None else np.ones(X.shape[0])
    probabilities = probabilities if probabilities is not None else np.ones(X.shape[0])
    # Black removed and is used for noise instead.
    unique_labels = set(labels)
    colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
    # The probability of a point belonging to its labeled cluster determines
    # the size of its marker
    proba_map = {idx: probabilities[idx] for idx in range(len(labels))}
    for k, col in zip(unique_labels, colors):
        if k == -1:
            # Black used for noise.
            col = [0, 0, 0, 1]

        class_index = (labels == k).nonzero()[0]
        for ci in class_index:
            ax.plot(
                X[ci, 0],
                X[ci, 1],
                "x" if k == -1 else "o",
                markerfacecolor=tuple(col),
                markeredgecolor="k",
                markersize=4 if k == -1 else 1 + 5 * proba_map[ci],
            )
    n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
    preamble = "True" if ground_truth else "Estimated"
    title = f"{preamble} number of clusters: {n_clusters_}"
    if parameters is not None:
        parameters_str = ", ".join(f"{k}={v}" for k, v in parameters.items())
        title += f" | {parameters_str}"
    ax.set_title(title)
    plt.tight_layout()

Сгенерировать тестовые данные#

Одним из наибольших преимуществ HDBSCAN перед DBSCAN является его устойчивость из коробки. Это особенно заметно на неоднородных смесях данных. Как и DBSCAN, он может моделировать произвольные формы и распределения, однако, в отличие от DBSCAN, он не требует указания произвольного и чувствительного eps гиперпараметр.

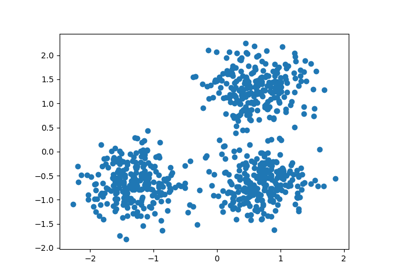
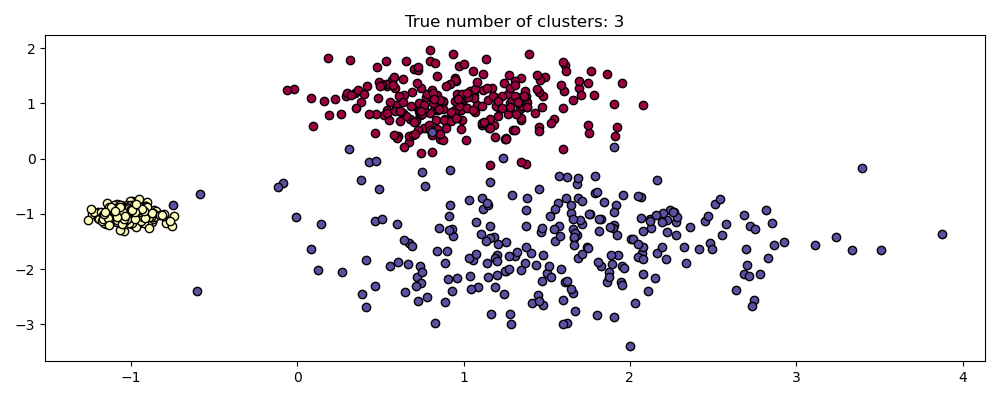
Например, ниже мы генерируем набор данных из смеси трех двумерных и изотропных гауссовских распределений.

centers = [[1, 1], [-1, -1], [1.5, -1.5]]
X, labels_true = make_blobs(
    n_samples=750, centers=centers, cluster_std=[0.4, 0.1, 0.75], random_state=0
)
plot(X, labels=labels_true, ground_truth=True)

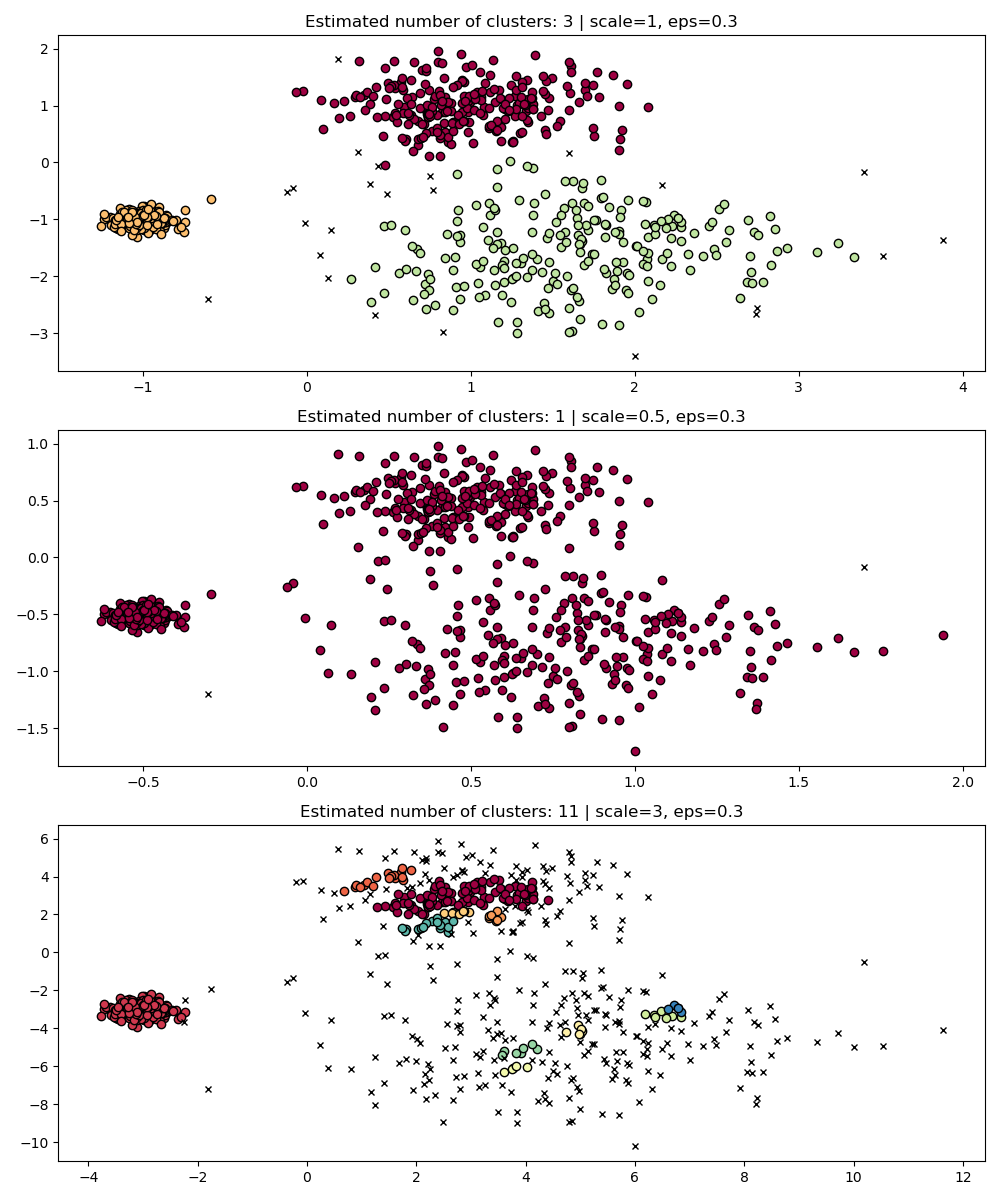
Инвариантность к масштабу#

Стоит помнить, что хотя DBSCAN предоставляет значение по умолчанию для eps параметр, он практически не имеет подходящего значения по умолчанию и должен быть настроен для конкретного используемого набора данных.

В качестве простой демонстрации рассмотрим кластеризацию для eps значение, настроенное для одного набора данных, и кластеризация, полученная с тем же значением, но примененная к масштабированным версиям набора данных.

fig, axes = plt.subplots(3, 1, figsize=(10, 12))
dbs = DBSCAN(eps=0.3)
for idx, scale in enumerate([1, 0.5, 3]):
    dbs.fit(X * scale)
    plot(X * scale, dbs.labels_, parameters={"scale": scale, "eps": 0.3}, ax=axes[idx])

Estimated number of clusters: 3 | scale=1, eps=0.3, Estimated number of clusters: 1 | scale=0.5, eps=0.3, Estimated number of clusters: 11 | scale=3, eps=0.3

Действительно, чтобы сохранить те же результаты, нам пришлось бы масштабировать eps на тот же коэффициент.

fig, axis = plt.subplots(1, 1, figsize=(12, 5))
dbs = DBSCAN(eps=0.9).fit(3 * X)
plot(3 * X, dbs.labels_, parameters={"scale": 3, "eps": 0.9}, ax=axis)

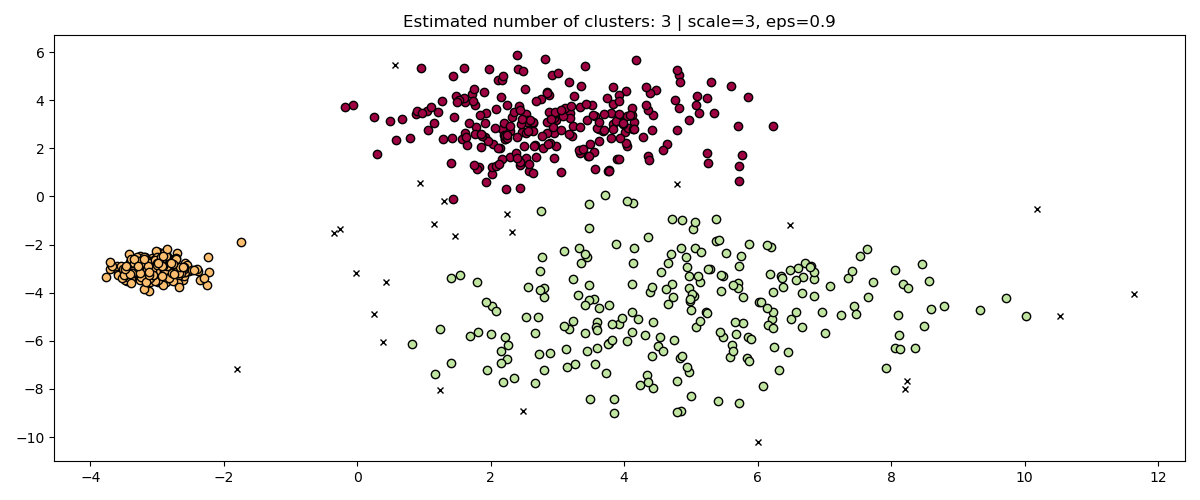
Estimated number of clusters: 3 | scale=3, eps=0.9

При стандартизации данных (например, с использованием sklearn.preprocessing.StandardScaler) помогает смягчить эту проблему, необходимо проявлять большую осторожность при выборе подходящего значения для eps.

HDBSCAN гораздо более устойчив в этом смысле: HDBSCAN можно рассматривать как кластеризацию по всем возможным значениям eps и извлечение лучших кластеров из всех возможных кластеров (см. Руководство пользователя). Одно непосредственное преимущество заключается в том, что HDBSCAN инвариантен к масштабу.

fig, axes = plt.subplots(3, 1, figsize=(10, 12))
hdb = HDBSCAN(copy=True)
for idx, scale in enumerate([1, 0.5, 3]):
    hdb.fit(X * scale)
    plot(
        X * scale,
        hdb.labels_,
        hdb.probabilities_,
        ax=axes[idx],
        parameters={"scale": scale},
    )

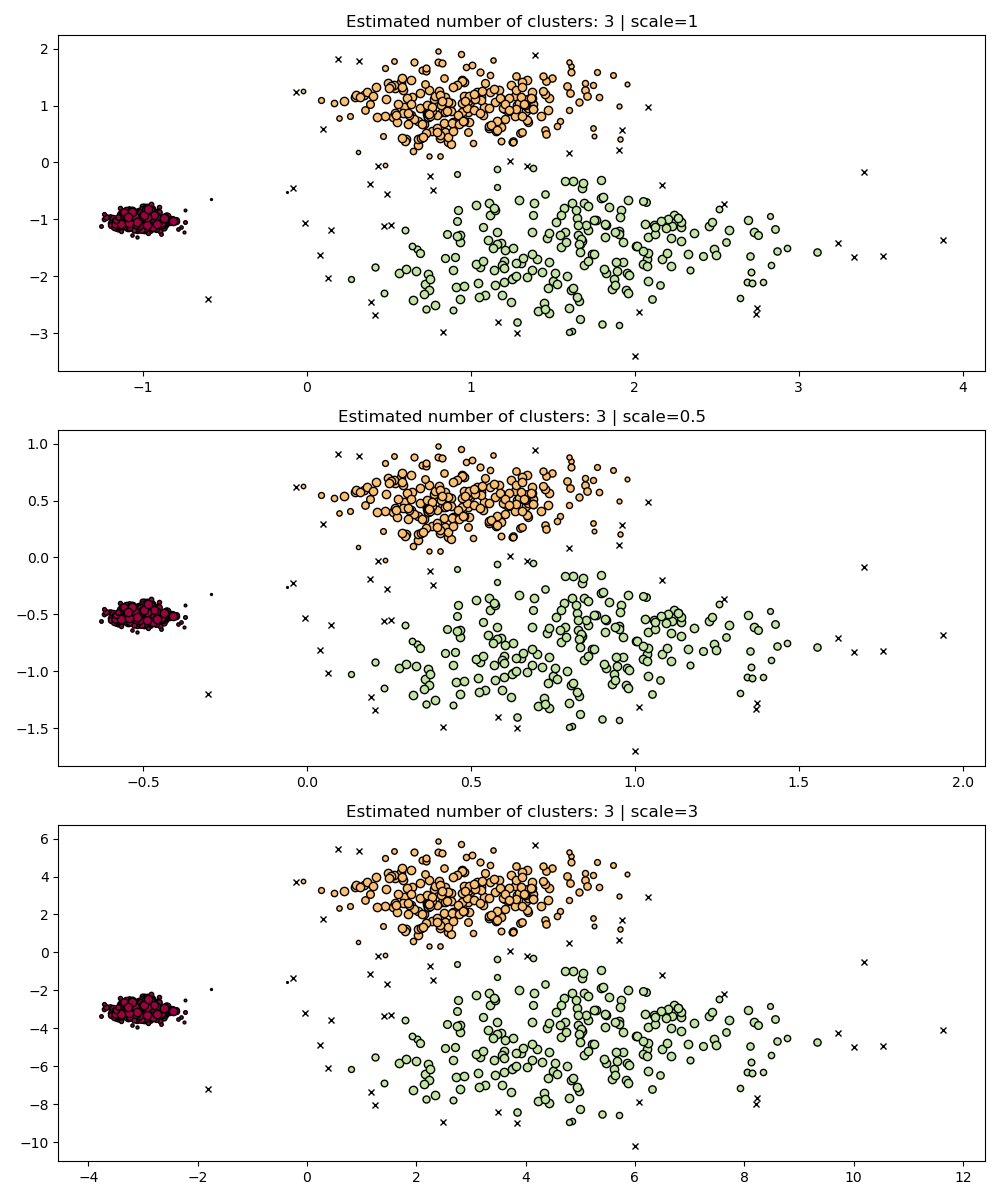
Estimated number of clusters: 3 | scale=1, Estimated number of clusters: 3 | scale=0.5, Estimated number of clusters: 3 | scale=3

Кластеризация на нескольких масштабах#

HDBSCAN гораздо более чем инвариантен к масштабу — он способен к многомасштабной кластеризации, что учитывает кластеры с различной плотностью. Традиционный DBSCAN предполагает, что любые потенциальные кластеры однородны по плотности. HDBSCAN свободен от таких ограничений. Чтобы продемонстрировать это, рассмотрим следующий набор данных

centers = [[-0.85, -0.85], [-0.85, 0.85], [3, 3], [3, -3]]
X, labels_true = make_blobs(
    n_samples=750, centers=centers, cluster_std=[0.2, 0.35, 1.35, 1.35], random_state=0
)
plot(X, labels=labels_true, ground_truth=True)

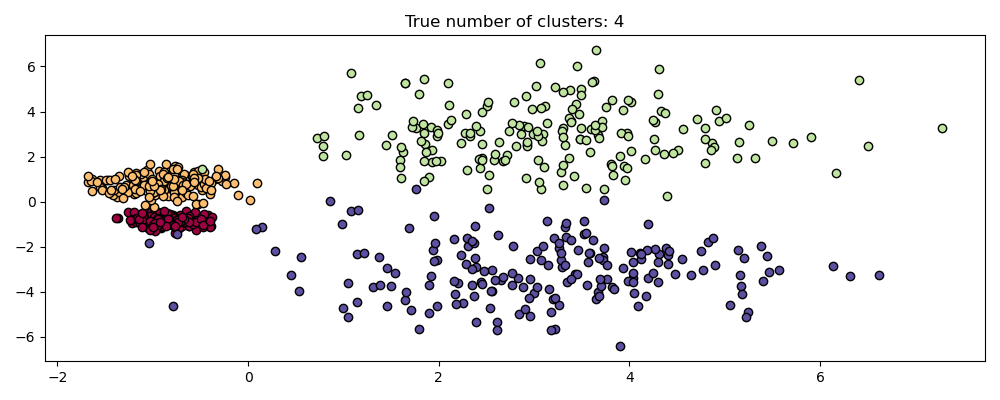
Этот набор данных сложнее для DBSCAN из-за различных плотностей и пространственного разделения:

Если eps слишком велико, то мы рискуем ложно объединить два плотных кластера в один, поскольку их взаимная достижимость будет расширять кластеры.
Если eps слишком мал, то мы рискуем раздробить более разреженные кластеры на множество ложных кластеров.

Не говоря уже о том, что это требует ручной настройки выбора eps пока не найдем компромисс, с которым мы согласны.

fig, axes = plt.subplots(2, 1, figsize=(10, 8))
params = {"eps": 0.7}
dbs = DBSCAN(**params).fit(X)
plot(X, dbs.labels_, parameters=params, ax=axes[0])
params = {"eps": 0.3}
dbs = DBSCAN(**params).fit(X)
plot(X, dbs.labels_, parameters=params, ax=axes[1])

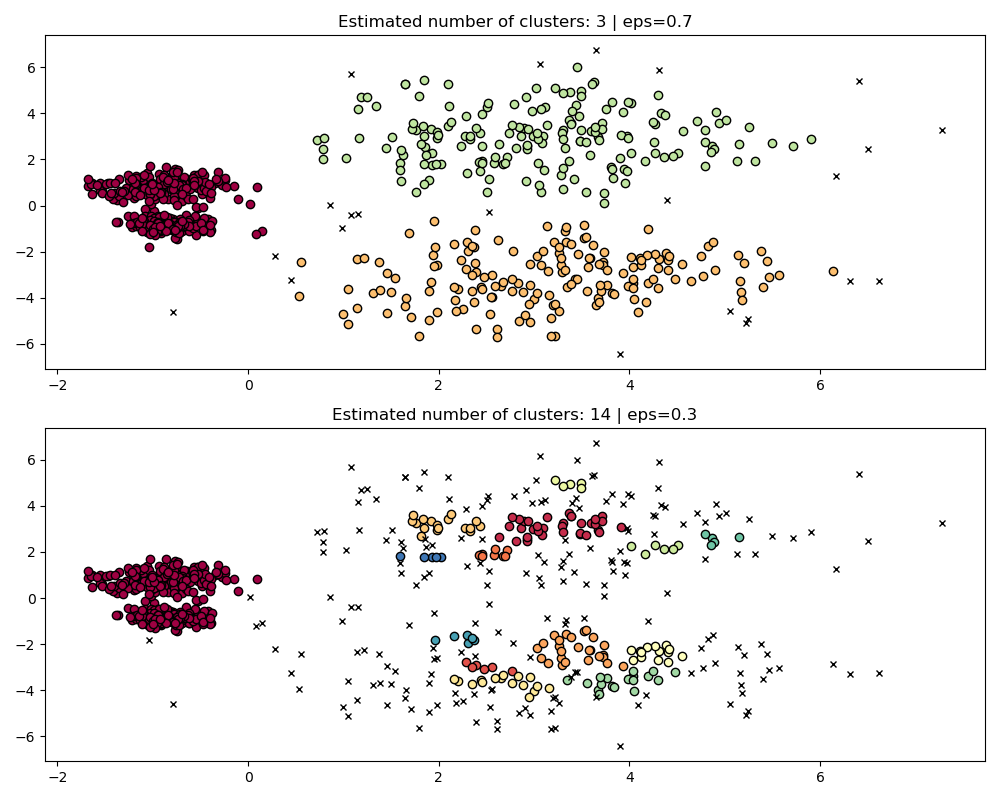
Estimated number of clusters: 3 | eps=0.7, Estimated number of clusters: 14 | eps=0.3

Для правильной кластеризации двух плотных кластеров потребуется меньшее значение epsilon, однако при eps=0.3 мы уже фрагментируем разреженные кластеры, что станет только более выраженным при уменьшении эпсилон. Действительно, кажется, что DBSCAN не способен одновременно разделить два плотных кластера и предотвратить фрагментацию разреженных кластеров. Сравним с HDBSCAN.

hdb = HDBSCAN(copy=True).fit(X)
plot(X, hdb.labels_, hdb.probabilities_)

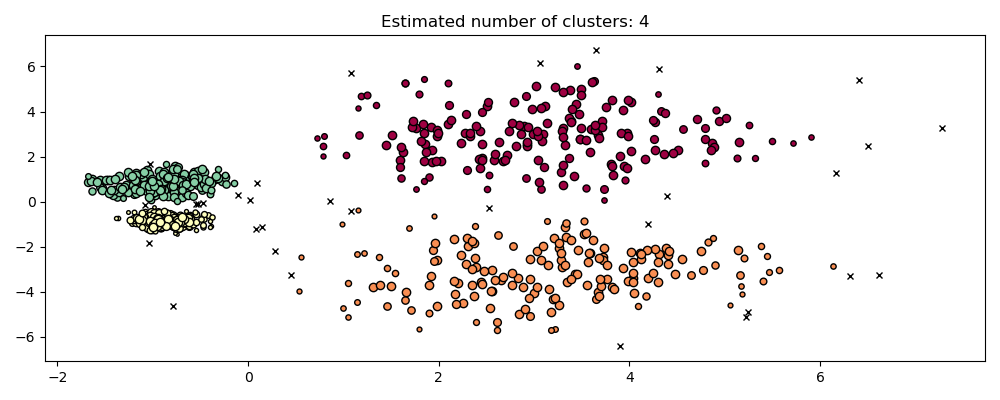
HDBSCAN способен адаптироваться к многоуровневой структуре набора данных без необходимости настройки параметров. Хотя любой достаточно интересный набор данных потребует настройки, этот случай демонстрирует, что HDBSCAN может давать качественно лучшие классы кластеризации без вмешательства пользователей, которые недоступны через DBSCAN.

Робастность гиперпараметров#

В конечном итоге настройка будет важным шагом в любом реальном приложении, поэтому давайте рассмотрим некоторые из наиболее важных гиперпараметров для HDBSCAN. Хотя HDBSCAN свободен от eps параметр DBSCAN, он все еще имеет некоторые гиперпараметры, такие как min_cluster_size и min_samples которые настраивают его результаты относительно плотности. Однако мы увидим, что HDBSCAN относительно устойчив к различным реальным примерам благодаря этим параметрам, чей ясный смысл помогает их настройке.

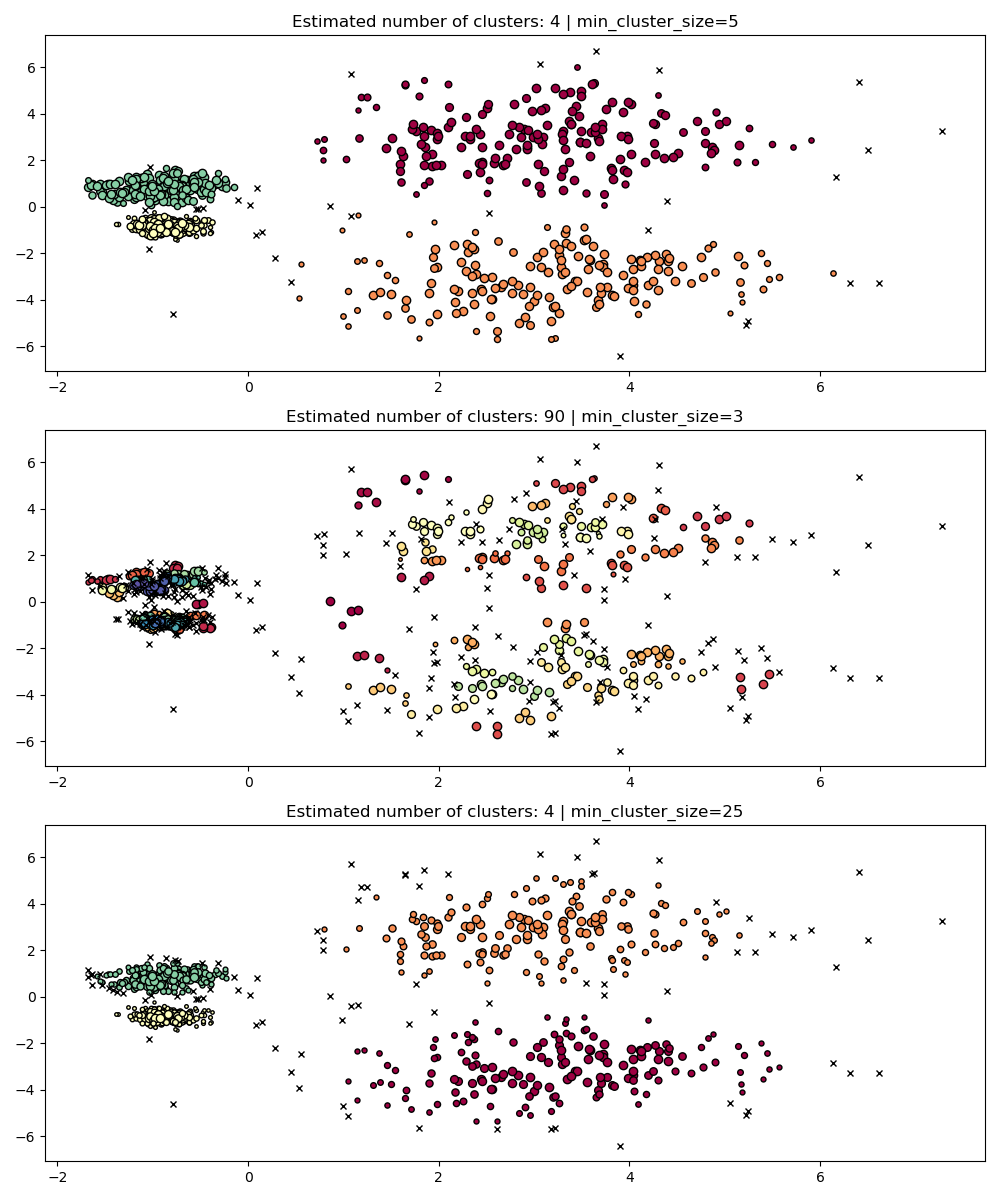
`min_cluster_size`#

min_cluster_size — это минимальное количество образцов в группе, чтобы эта группа считалась кластером.

Кластеры меньше этого размера будут оставлены как шум. Значение по умолчанию — 5. Этот параметр обычно настраивается на большие значения по мере необходимости. Меньшие значения, вероятно, приведут к результатам с меньшим количеством точек, помеченных как шум. Однако слишком маленькие значения приведут к ложному выделению и предпочтению подкластеров. Большие значения, как правило, более устойчивы к зашумлённым наборам данных, например, кластерам с высокой дисперсией и значительным перекрытием.

PARAM = ({"min_cluster_size": 5}, {"min_cluster_size": 3}, {"min_cluster_size": 25})
fig, axes = plt.subplots(3, 1, figsize=(10, 12))
for i, param in enumerate(PARAM):
    hdb = HDBSCAN(copy=True, **param).fit(X)
    labels = hdb.labels_

    plot(X, labels, hdb.probabilities_, param, ax=axes[i])

Estimated number of clusters: 4 | min_cluster_size=5, Estimated number of clusters: 90 | min_cluster_size=3, Estimated number of clusters: 4 | min_cluster_size=25

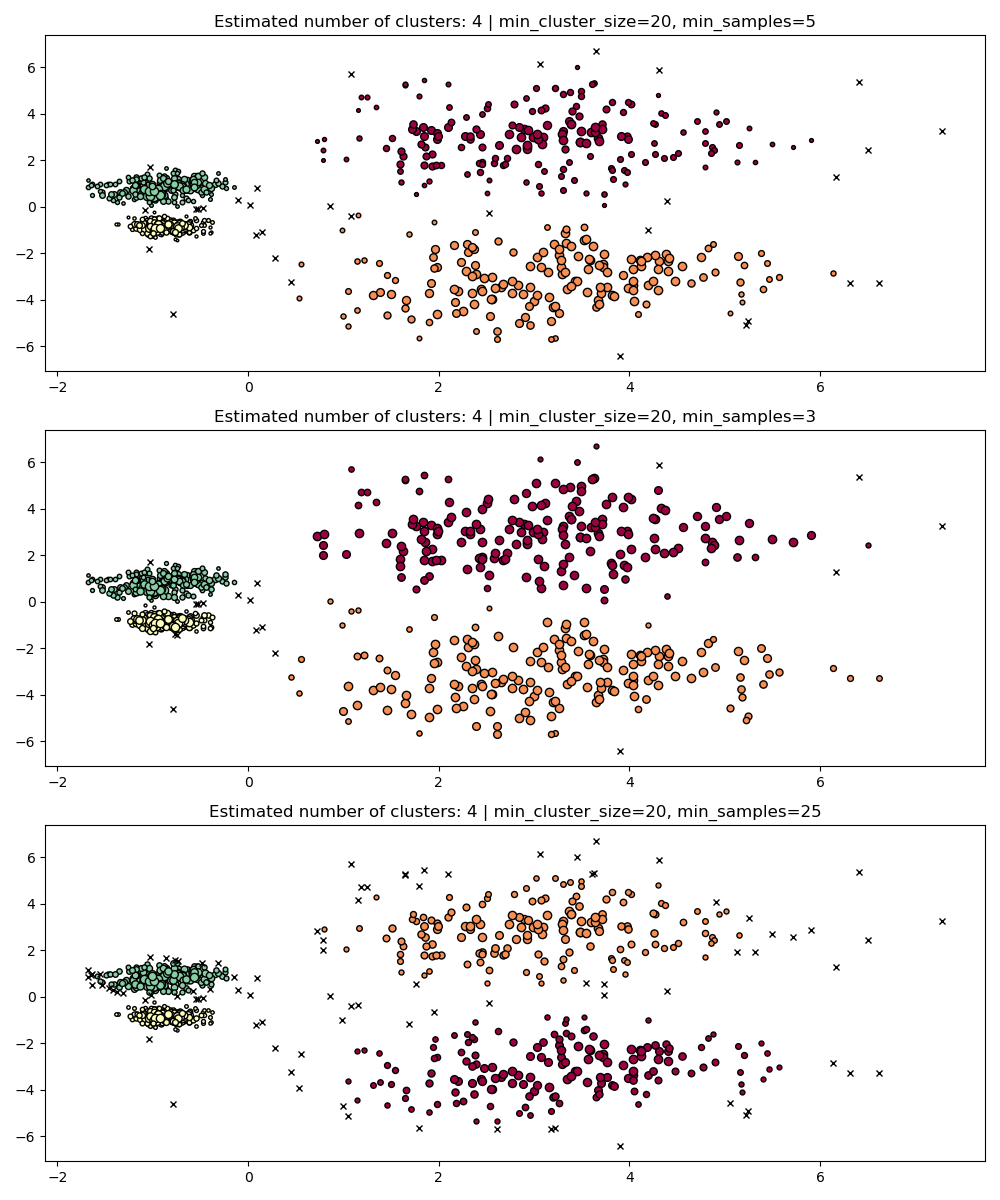
`min_samples`#

min_samples — это количество образцов в окрестности точки, чтобы она считалась центральной точкой, включая саму точку. min_samples по умолчанию min_cluster_size. Аналогично min_cluster_size, большие значения для min_samples увеличивает устойчивость модели к шуму, но рискует игнорировать или отбрасывать потенциально валидные, но маленькие кластеры. min_samples лучше настроить после нахождения хорошего значения для min_cluster_size.

PARAM = (
    {"min_cluster_size": 20, "min_samples": 5},
    {"min_cluster_size": 20, "min_samples": 3},
    {"min_cluster_size": 20, "min_samples": 25},
)
fig, axes = plt.subplots(3, 1, figsize=(10, 12))
for i, param in enumerate(PARAM):
    hdb = HDBSCAN(copy=True, **param).fit(X)
    labels = hdb.labels_

    plot(X, labels, hdb.probabilities_, param, ax=axes[i])

Estimated number of clusters: 4 | min_cluster_size=20, min_samples=5, Estimated number of clusters: 4 | min_cluster_size=20, min_samples=3, Estimated number of clusters: 4 | min_cluster_size=20, min_samples=25

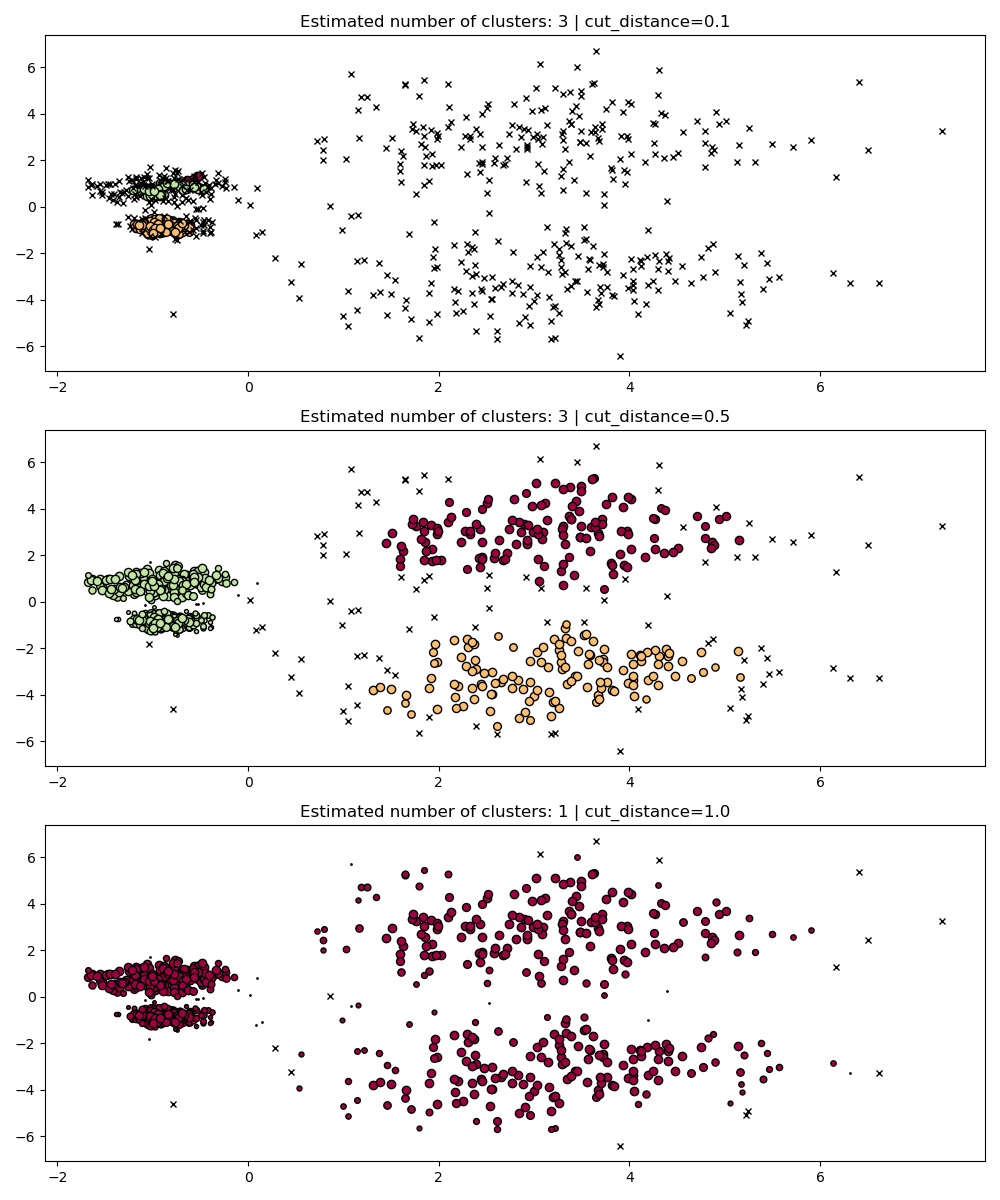
`dbscan_clustering`#

Во время fit, HDBSCAN строит дерево одиночной связи, которое кодирует кластеризацию всех точек для всех значений DBSCAN’s eps параметр. Таким образом, мы можем эффективно строить графики и оценивать эти кластеризации без полного пересчета промежуточных значений, таких как core-distances, mutual-reachability и минимальное остовное дерево. Все, что нам нужно сделать, это указать cut_distance (эквивалентно eps) мы хотим кластеризовать.

PARAM = (
    {"cut_distance": 0.1},
    {"cut_distance": 0.5},
    {"cut_distance": 1.0},
)
hdb = HDBSCAN(copy=True)
hdb.fit(X)
fig, axes = plt.subplots(len(PARAM), 1, figsize=(10, 12))
for i, param in enumerate(PARAM):
    labels = hdb.dbscan_clustering(**param)

    plot(X, labels, hdb.probabilities_, param, ax=axes[i])