Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Иерархическая кластеризация со структурой и без#
Этот пример демонстрирует иерархическую кластеризацию с ограничениями связности и без них. Он показывает эффект наложения графа связности для захвата локальной структуры в данных. Без ограничений связности кластеризация основана исключительно на расстоянии, в то время как с ограничениями кластеризация учитывает локальную структуру.
Для получения дополнительной информации см. Иерархическая кластеризация.
Есть два преимущества наложения связности. Во-первых, кластеризация с разреженными матрицами связности обычно быстрее.
Во-вторых, при использовании матрицы связности, одиночная, средняя и полная связи нестабильны и склонны создавать несколько кластеров, которые растут очень быстро. Действительно, средняя и полная связи борются с этим поведением перколяции, рассматривая все расстояния между двумя кластерами при их слиянии (в то время как одиночная связь преувеличивает это поведение, рассматривая только кратчайшее расстояние между кластерами). Граф связности нарушает этот механизм для средней и полной связей, делая их похожими на более хрупкую одиночную связь. Этот эффект более выражен для очень разреженных графов (попробуйте уменьшить количество соседей в kneighbors_graph) и с полной связью. В частности, наличие очень малого числа соседей в графе накладывает геометрию, близкую к одиночной связи, которая, как хорошо известно, имеет эту неустойчивость перколяции.
Эффект наложения связности проиллюстрирован на двух различных, но похожих наборах данных, которые демонстрируют спиральную структуру. В первом примере мы строим набор данных Swiss roll и запускаем иерархическую кластеризацию на позициях данных. Здесь мы сравниваем неструктурированную кластеризацию Уорда со структурированным вариантом, который обеспечивает связность k-ближайших соседей. Во втором примере мы включаем эффекты применения такого графа связности к одиночной, средней и полной связи.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
для отчета.#
import time
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_swiss_roll
n_samples = 1500
noise = 0.05
X1, _ = make_swiss_roll(n_samples, noise=noise)
X1[:, 1] *= 0.5 # Make the roll thinner
Вычисление кластеризации без ограничений связности#
print("Compute unstructured hierarchical clustering...")
st = time.time()
ward_unstructured = AgglomerativeClustering(n_clusters=6, linkage="ward").fit(X1)
elapsed_time_unstructured = time.time() - st
label_unstructured = ward_unstructured.labels_
print(f"Elapsed time: {elapsed_time_unstructured:.2f}s")
print(f"Number of points: {label_unstructured.size}")
Compute unstructured hierarchical clustering...
Elapsed time: 0.04s
Number of points: 1500
Построить результат неструктурированной кластеризации
import matplotlib.pyplot as plt
import numpy as np
fig1 = plt.figure()
ax1 = fig1.add_subplot(111, projection="3d", elev=7, azim=-80)
ax1.set_position([0, 0, 0.95, 1])
for l in np.unique(label_unstructured):
ax1.scatter(
X1[label_unstructured == l, 0],
X1[label_unstructured == l, 1],
X1[label_unstructured == l, 2],
color=plt.cm.jet(float(l) / np.max(label_unstructured + 1)),
s=20,
edgecolor="k",
)
_ = fig1.suptitle(
f"Without connectivity constraints (time {elapsed_time_unstructured:.2f}s)"
)

Вычисление кластеризации с ограничениями связности#
from sklearn.neighbors import kneighbors_graph
connectivity = kneighbors_graph(X1, n_neighbors=10, include_self=False)
print("Compute structured hierarchical clustering...")
st = time.time()
ward_structured = AgglomerativeClustering(
n_clusters=6, connectivity=connectivity, linkage="ward"
).fit(X1)
elapsed_time_structured = time.time() - st
label_structured = ward_structured.labels_
print(f"Elapsed time: {elapsed_time_structured:.2f}s")
print(f"Number of points: {label_structured.size}")
Compute structured hierarchical clustering...
Elapsed time: 0.06s
Number of points: 1500
Построить результат структурированной кластеризации
fig2 = plt.figure()
ax2 = fig2.add_subplot(111, projection="3d", elev=7, azim=-80)
ax2.set_position([0, 0, 0.95, 1])
for l in np.unique(label_structured):
ax2.scatter(
X1[label_structured == l, 0],
X1[label_structured == l, 1],
X1[label_structured == l, 2],
color=plt.cm.jet(float(l) / np.max(label_structured + 1)),
s=20,
edgecolor="k",
)
_ = fig2.suptitle(
f"With connectivity constraints (time {elapsed_time_structured:.2f}s)"
)

Сгенерировать двумерный спиральный набор данных.#
n_samples = 1500
np.random.seed(0)
t = 1.5 * np.pi * (1 + 3 * np.random.rand(1, n_samples))
x = t * np.cos(t)
y = t * np.sin(t)
X2 = np.concatenate((x, y))
X2 += 0.7 * np.random.randn(2, n_samples)
X2 = X2.T
Захват локальной связности с использованием графа#
Большее количество соседей даст более однородные кластеры ценой увеличения времени вычислений. Очень большое количество соседей дает более равномерно распределенные размеры кластеров, но может не учитывать локальную структуру многообразия данных.
knn_graph = kneighbors_graph(X2, 30, include_self=False)
Построить кластеризацию со структурой и без#
fig3 = plt.figure(figsize=(8, 12))
subfigs = fig3.subfigures(4, 1)
params = [
(None, 30),
(None, 3),
(knn_graph, 30),
(knn_graph, 3),
]
for subfig, (connectivity, n_clusters) in zip(subfigs, params):
axs = subfig.subplots(1, 4, sharey=True)
for index, linkage in enumerate(("average", "complete", "ward", "single")):
model = AgglomerativeClustering(
linkage=linkage, connectivity=connectivity, n_clusters=n_clusters
)
t0 = time.time()
model.fit(X2)
elapsed_time = time.time() - t0
axs[index].scatter(
X2[:, 0], X2[:, 1], c=model.labels_, cmap=plt.cm.nipy_spectral
)
axs[index].set_title(
"linkage=%s\n(time %.2fs)" % (linkage, elapsed_time),
fontdict=dict(verticalalignment="top"),
)
axs[index].set_aspect("equal")
axs[index].axis("off")
subfig.subplots_adjust(bottom=0, top=0.83, wspace=0, left=0, right=1)
subfig.suptitle(
"n_cluster=%i, connectivity=%r" % (n_clusters, connectivity is not None),
size=17,
)
plt.show()

Общее время выполнения скрипта: (0 минут 2.094 секунды)
Связанные примеры

Демонстрация структурированной иерархической кластеризации Уорда на изображении монет
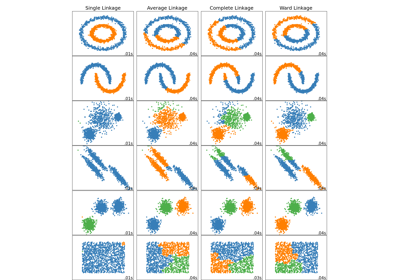
Сравнение различных методов иерархической связи на игрушечных наборах данных
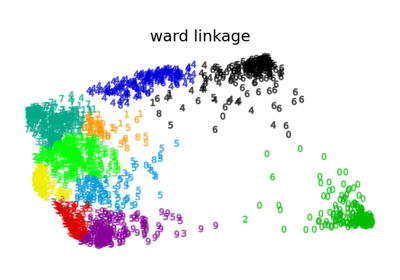
Различные агломеративные кластеризации на 2D-вложении цифр
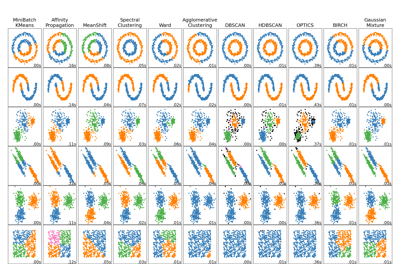
Сравнение различных алгоритмов кластеризации на игрушечных наборах данных