Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Демонстрация кластеризации K-Means на данных рукописных цифр#
В этом примере мы сравниваем различные стратегии инициализации для K-means с точки зрения времени выполнения и качества результатов.
Поскольку истинные значения здесь известны, мы также применяем различные метрики качества кластеризации для оценки соответствия меток кластеров истинным значениям.
Метрики качества кластеризации, оцененные (см. Оценка производительности кластеризации для определений и обсуждения метрик:
Сокращение |
полное имя |
|---|---|
homo |
оценка однородности |
compl |
оценка полноты |
v-мера |
Мера V |
ARI |
скорректированный индекс Рэнда |
AMI |
скорректированная взаимная информация |
силуэт |
коэффициент силуэта |
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Загрузить набор данных#
Мы начнем с загрузки digits набор данных. Этот набор данных содержит рукописные цифры от 0 до 9. В контексте кластеризации хотелось бы сгруппировать изображения так, чтобы рукописные цифры на изображении были одинаковыми.
import numpy as np
from sklearn.datasets import load_digits
data, labels = load_digits(return_X_y=True)
(n_samples, n_features), n_digits = data.shape, np.unique(labels).size
print(f"# digits: {n_digits}; # samples: {n_samples}; # features {n_features}")
# digits: 10; # samples: 1797; # features 64
Определим наш эталон оценки#
Сначала мы проведем наш оценочный тест. В ходе этого теста мы намерены сравнить различные методы инициализации для KMeans. Наш тест будет:
создать конвейер, который будет масштабировать данные с помощью
StandardScaler;обучать и измерять время обучения конвейера;
измерить производительность кластеризации с помощью различных метрик.
from time import time
from sklearn import metrics
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
def bench_k_means(kmeans, name, data, labels):
"""Benchmark to evaluate the KMeans initialization methods.
Parameters
----------
kmeans : KMeans instance
A :class:`~sklearn.cluster.KMeans` instance with the initialization
already set.
name : str
Name given to the strategy. It will be used to show the results in a
table.
data : ndarray of shape (n_samples, n_features)
The data to cluster.
labels : ndarray of shape (n_samples,)
The labels used to compute the clustering metrics which requires some
supervision.
"""
t0 = time()
estimator = make_pipeline(StandardScaler(), kmeans).fit(data)
fit_time = time() - t0
results = [name, fit_time, estimator[-1].inertia_]
# Define the metrics which require only the true labels and estimator
# labels
clustering_metrics = [
metrics.homogeneity_score,
metrics.completeness_score,
metrics.v_measure_score,
metrics.adjusted_rand_score,
metrics.adjusted_mutual_info_score,
]
results += [m(labels, estimator[-1].labels_) for m in clustering_metrics]
# The silhouette score requires the full dataset
results += [
metrics.silhouette_score(
data,
estimator[-1].labels_,
metric="euclidean",
sample_size=300,
)
]
# Show the results
formatter_result = (
"{:9s}\t{:.3f}s\t{:.0f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}"
)
print(formatter_result.format(*results))
Запустить бенчмарк#
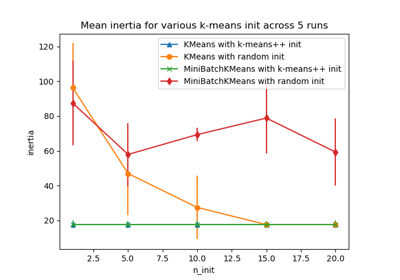
Мы сравним три подхода:
инициализация с использованием
k-means++. Этот метод стохастический, и мы запустим инициализацию 4 раза;случайную инициализацию. Этот метод также стохастический, и мы запустим инициализацию 4 раза;
Инвариантность относительно распространенности
PCAпроекции. Действительно, мы будем использовать компонентыPCAдля инициализации KMeans. Этот метод является детерминированным, и достаточно одной инициализации.
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
print(82 * "_")
print("init\t\ttime\tinertia\thomo\tcompl\tv-meas\tARI\tAMI\tsilhouette")
kmeans = KMeans(init="k-means++", n_clusters=n_digits, n_init=4, random_state=0)
bench_k_means(kmeans=kmeans, name="k-means++", data=data, labels=labels)
kmeans = KMeans(init="random", n_clusters=n_digits, n_init=4, random_state=0)
bench_k_means(kmeans=kmeans, name="random", data=data, labels=labels)
pca = PCA(n_components=n_digits).fit(data)
kmeans = KMeans(init=pca.components_, n_clusters=n_digits, n_init=1)
bench_k_means(kmeans=kmeans, name="PCA-based", data=data, labels=labels)
print(82 * "_")
__________________________________________________________________________________
init time inertia homo compl v-meas ARI AMI silhouette
k-means++ 0.033s 69545 0.598 0.645 0.621 0.469 0.617 0.158
random 0.038s 69735 0.681 0.723 0.701 0.574 0.698 0.173
PCA-based 0.013s 69513 0.600 0.647 0.622 0.468 0.618 0.162
__________________________________________________________________________________
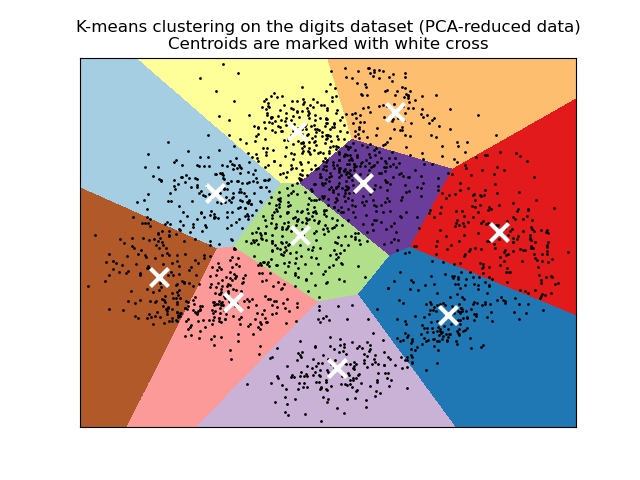
Визуализируйте результаты на данных, приведенных к PCA#
PCA позволяет проецировать данные из исходного 64-мерного пространства в пространство меньшей размерности. Затем мы можем использовать PCA спроецировать в
2-мерное пространство и построить данные и кластеры в этом новом пространстве.
import matplotlib.pyplot as plt
reduced_data = PCA(n_components=2).fit_transform(data)
kmeans = KMeans(init="k-means++", n_clusters=n_digits, n_init=4)
kmeans.fit(reduced_data)
# Step size of the mesh. Decrease to increase the quality of the VQ.
h = 0.02 # point in the mesh [x_min, x_max]x[y_min, y_max].
# Plot the decision boundary. For that, we will assign a color to each
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Obtain labels for each point in mesh. Use last trained model.
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure(1)
plt.clf()
plt.imshow(
Z,
interpolation="nearest",
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap=plt.cm.Paired,
aspect="auto",
origin="lower",
)
plt.plot(reduced_data[:, 0], reduced_data[:, 1], "k.", markersize=2)
# Plot the centroids as a white X
centroids = kmeans.cluster_centers_
plt.scatter(
centroids[:, 0],
centroids[:, 1],
marker="x",
s=169,
linewidths=3,
color="w",
zorder=10,
)
plt.title(
"K-means clustering on the digits dataset (PCA-reduced data)\n"
"Centroids are marked with white cross"
)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.show()
Общее время выполнения скрипта: (0 минут 2.990 секунд)
Связанные примеры
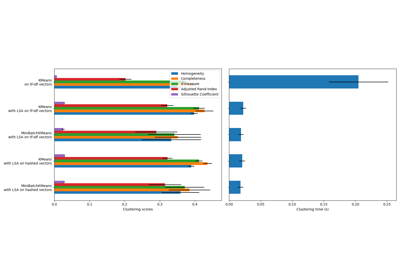
Кластеризация текстовых документов с использованием k-means
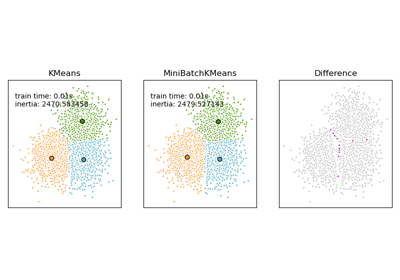
Сравнение алгоритмов кластеризации K-Means и MiniBatchKMeans