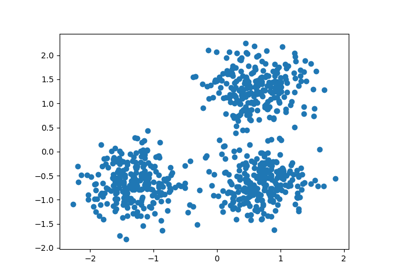
adjusted_rand_score#
- sklearn.metrics.adjusted_rand_score(labels_true, labels_pred)[источник]#
Индекс Рэнда, скорректированный на случайность.
Индекс Рэнда вычисляет меру сходства между двумя кластеризациями, рассматривая все пары образцов и подсчитывая пары, которые назначены в одинаковые или разные кластеры в предсказанной и истинной кластеризациях.
Сырой показатель RI затем "корректируется на случайность" в показатель ARI с использованием следующей схемы:
ARI = (RI - Expected_RI) / (max(RI) - Expected_RI)
Скорректированный индекс Рэнда, таким образом, гарантированно имеет значение, близкое к 0.0 для случайной разметки независимо от количества кластеров и образцов и точно 1.0, когда кластеризации идентичны (с точностью до перестановки). Скорректированный индекс Рэнда ограничен снизу значением -0.5 для особенно несогласованных кластеризаций.
ARI является симметричной мерой:
adjusted_rand_score(a, b) == adjusted_rand_score(b, a)
Подробнее в Руководство пользователя.
- Параметры:
- labels_truearray-like формы (n_samples,), dtype=int
Истинные метки классов, используемые в качестве эталона.
- labels_predarray-like формы (n_samples,), dtype=int
Метки кластеров для оценки.
- Возвращает:
- ARIfloat
Оценка сходства от -0.5 до 1.0. Случайные разметки имеют ARI близкий к 0.0. 1.0 означает идеальное совпадение.
Смотрите также
adjusted_mutual_info_scoreAdjusted Mutual Information.
Ссылки
[Hubert1985]L. Hubert и P. Arabie, Comparing Partitions, Journal of Classification 1985 https://link.springer.com/article/10.1007%2FBF01908075
[Steinley2004]D. Steinley, Свойства скорректированного индекса Рэнда Хьюберта-Араби, Psychological Methods 2004
Примеры
Идеально совпадающие разметки имеют оценку 1, даже
>>> from sklearn.metrics.cluster import adjusted_rand_score >>> adjusted_rand_score([0, 0, 1, 1], [0, 0, 1, 1]) 1.0 >>> adjusted_rand_score([0, 0, 1, 1], [1, 1, 0, 0]) 1.0
Разметки, которые относят всех членов классов к одним и тем же кластерам, являются полными, но не всегда чистыми, поэтому штрафуются:
>>> adjusted_rand_score([0, 0, 1, 2], [0, 0, 1, 1]) 0.57
ARI симметричен, поэтому разметки, имеющие чистые кластеры с элементами из одних и тех же классов, но с ненужными разделениями, штрафуются:
>>> adjusted_rand_score([0, 0, 1, 1], [0, 0, 1, 2]) 0.57
Если элементы классов полностью разделены по разным кластерам, назначение полностью неполное, поэтому ARI очень низкий:
>>> adjusted_rand_score([0, 0, 0, 0], [0, 1, 2, 3]) 0.0
ARI может принимать отрицательное значение для особенно несогласованных меток, которые являются худшим выбором, чем ожидаемое значение случайных меток:
>>> adjusted_rand_score([0, 0, 1, 1], [0, 1, 0, 1]) -0.5
См. Коррекция на случайность в оценке производительности кластеризации для более подробного примера.
Примеры галереи#
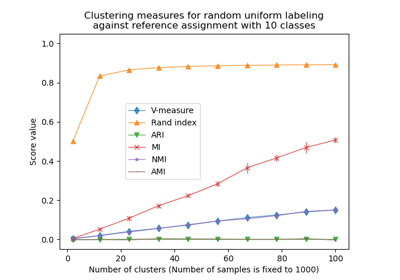
Коррекция на случайность в оценке производительности кластеризации
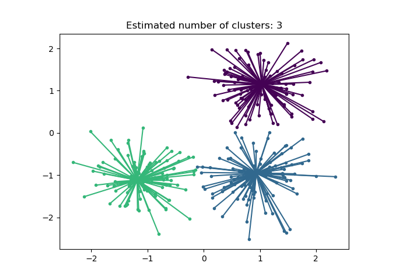
Демонстрация алгоритма кластеризации с распространением аффинности
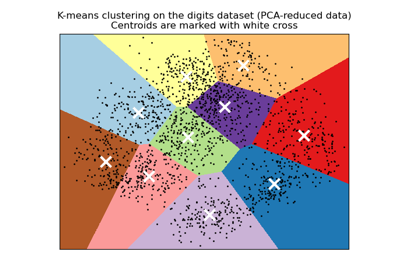
Демонстрация кластеризации K-Means на данных рукописных цифр
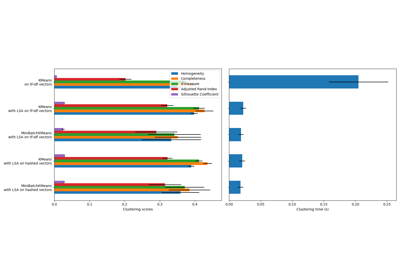
Кластеризация текстовых документов с использованием k-means