Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Демонстрация предположений k-means#
Этот пример предназначен для иллюстрации ситуаций, когда k-means создаёт неинтуитивные и, возможно, нежелательные кластеры.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Генерация данных#
Функция make_blobs генерирует изотропные (сферические) гауссовы сгустки. Для получения анизотропных (эллиптических) гауссовых сгустков необходимо определить линейное transformation.
import numpy as np
from sklearn.datasets import make_blobs
n_samples = 1500
random_state = 170
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
X_aniso = np.dot(X, transformation) # Anisotropic blobs
X_varied, y_varied = make_blobs(
n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=random_state
) # Unequal variance
X_filtered = np.vstack(
(X[y == 0][:500], X[y == 1][:100], X[y == 2][:10])
) # Unevenly sized blobs
y_filtered = [0] * 500 + [1] * 100 + [2] * 10
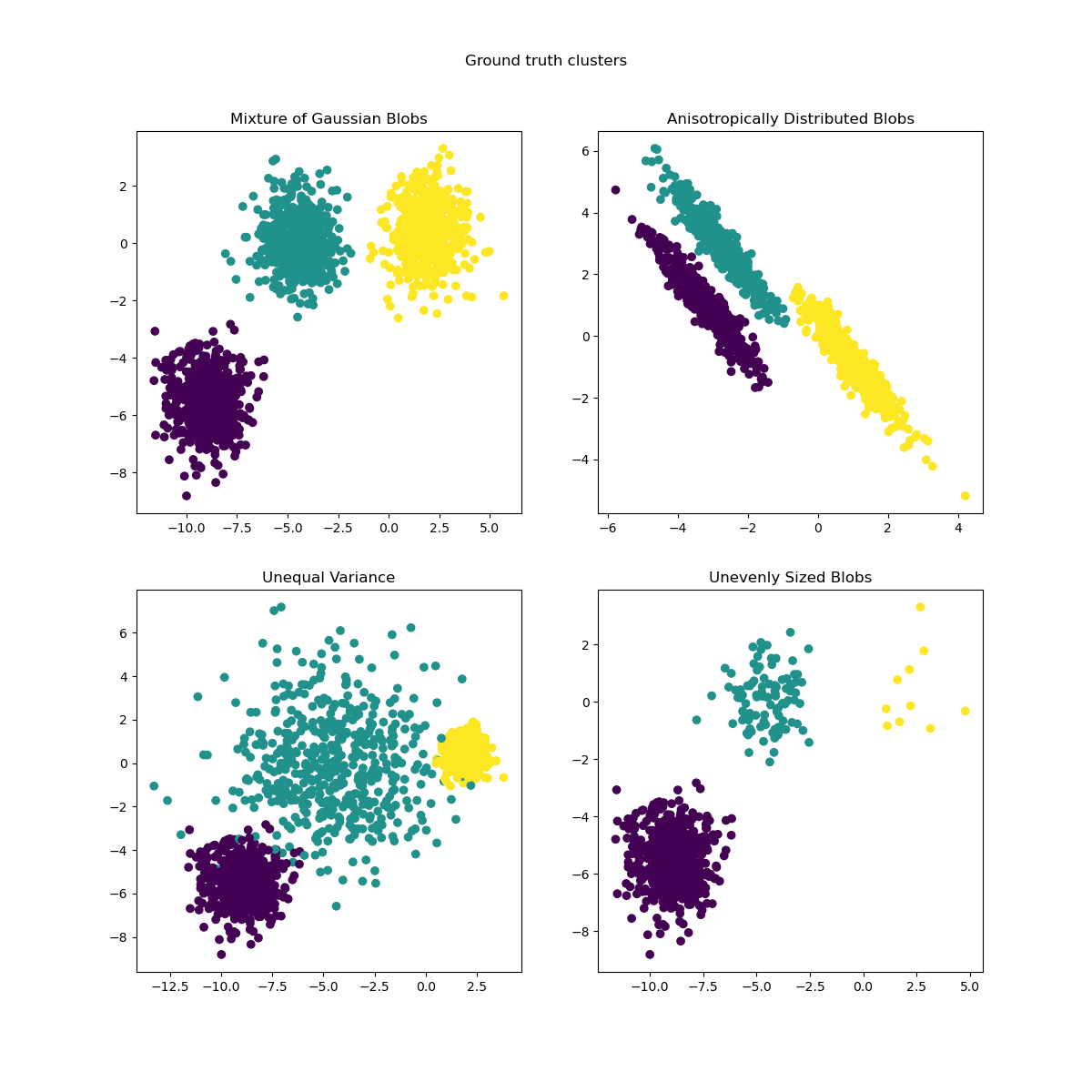
Мы можем визуализировать полученные данные:
import matplotlib.pyplot as plt
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))
axs[0, 0].scatter(X[:, 0], X[:, 1], c=y)
axs[0, 0].set_title("Mixture of Gaussian Blobs")
axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y)
axs[0, 1].set_title("Anisotropically Distributed Blobs")
axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_varied)
axs[1, 0].set_title("Unequal Variance")
axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_filtered)
axs[1, 1].set_title("Unevenly Sized Blobs")
plt.suptitle("Ground truth clusters").set_y(0.95)
plt.show()
Обучить модели и построить результаты#
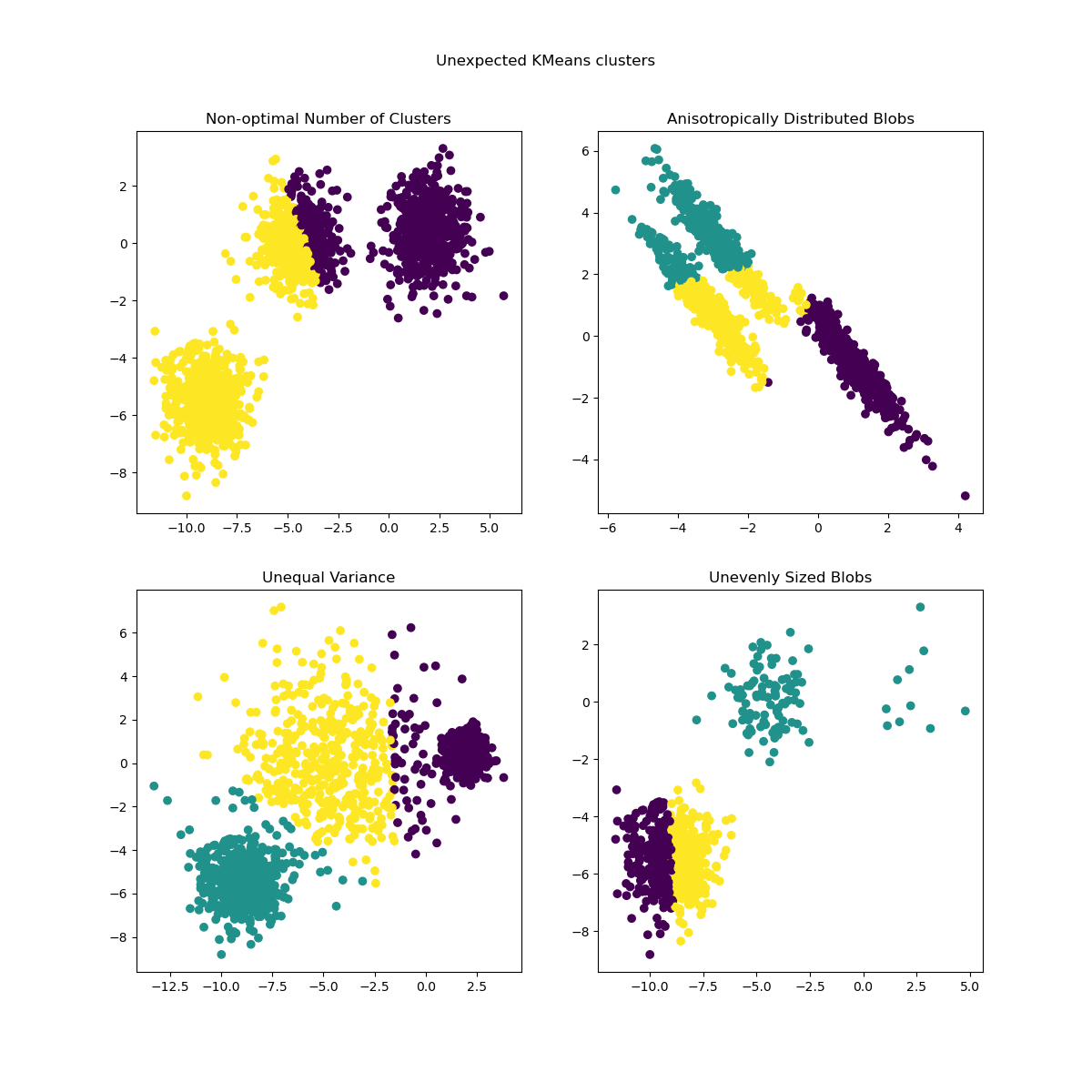
Ранее сгенерированные данные теперь используются, чтобы показать, как
KMeans ведет себя в следующих сценариях:
Неоптимальное количество кластеров: в реальных условиях нет однозначно определенного true количество кластеров. Подходящее количество кластеров должно быть определено на основе критериев, основанных на данных, и знаний о поставленной цели.
Анизотропно распределенные сгустки: k-средние состоит в минимизации евклидовых расстояний выборок до центроида кластера, к которому они отнесены. Как следствие, k-средние более подходит для кластеров, которые изотропны и нормально распределены (т.е. сферические гауссовы).
Неравная дисперсия: k-means эквивалентен взятию оценщика максимального правдоподобия для "смеси" k гауссовских распределений с одинаковыми дисперсиями, но, возможно, разными средними.
Неравномерные размеры кластеров: нет теоретического результата о k-средних, который утверждает, что для хорошей работы требуются кластеры схожего размера, однако минимизация евклидовых расстояний означает, что чем более разреженной и высокоразмерной является задача, тем больше необходимость запускать алгоритм с разными начальными центрами, чтобы обеспечить глобальный минимальный инерционный момент.
from sklearn.cluster import KMeans
common_params = {
"n_init": "auto",
"random_state": random_state,
}
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(12, 12))
y_pred = KMeans(n_clusters=2, **common_params).fit_predict(X)
axs[0, 0].scatter(X[:, 0], X[:, 1], c=y_pred)
axs[0, 0].set_title("Non-optimal Number of Clusters")
y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_aniso)
axs[0, 1].scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
axs[0, 1].set_title("Anisotropically Distributed Blobs")
y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_varied)
axs[1, 0].scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
axs[1, 0].set_title("Unequal Variance")
y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X_filtered)
axs[1, 1].scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
axs[1, 1].set_title("Unevenly Sized Blobs")
plt.suptitle("Unexpected KMeans clusters").set_y(0.95)
plt.show()
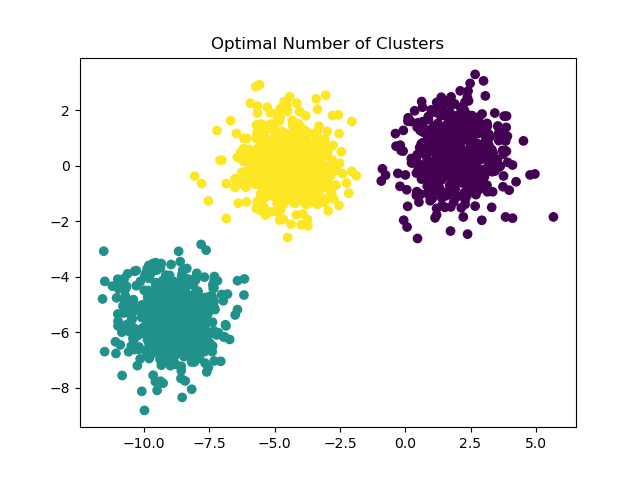
Возможные решения#
Пример того, как найти правильное количество кластеров, см.
Выбор количества кластеров с помощью анализа силуэта для кластеризации KMeans. В этом случае достаточно установить n_clusters=3.
y_pred = KMeans(n_clusters=3, **common_params).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Optimal Number of Clusters")
plt.show()
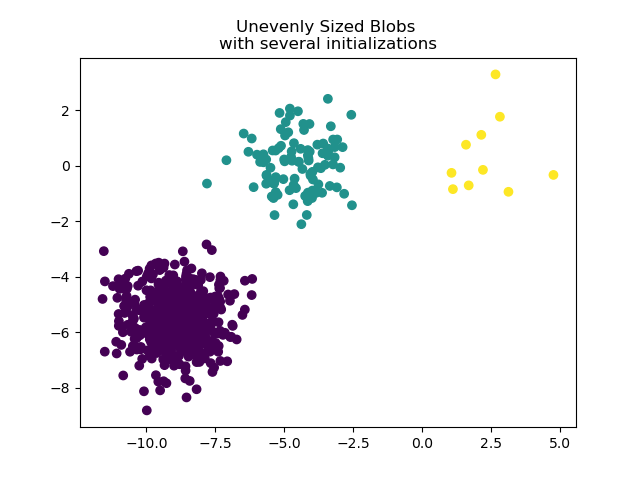
Для работы с неравномерно распределёнными сгустками можно увеличить количество случайных инициализаций. В этом случае мы устанавливаем n_init=10 чтобы избежать нахождения
субоптимального локального минимума. Для получения дополнительных сведений см. Кластеризация разреженных данных с помощью k-средних.
y_pred = KMeans(n_clusters=3, n_init=10, random_state=random_state).fit_predict(
X_filtered
)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs \nwith several initializations")
plt.show()
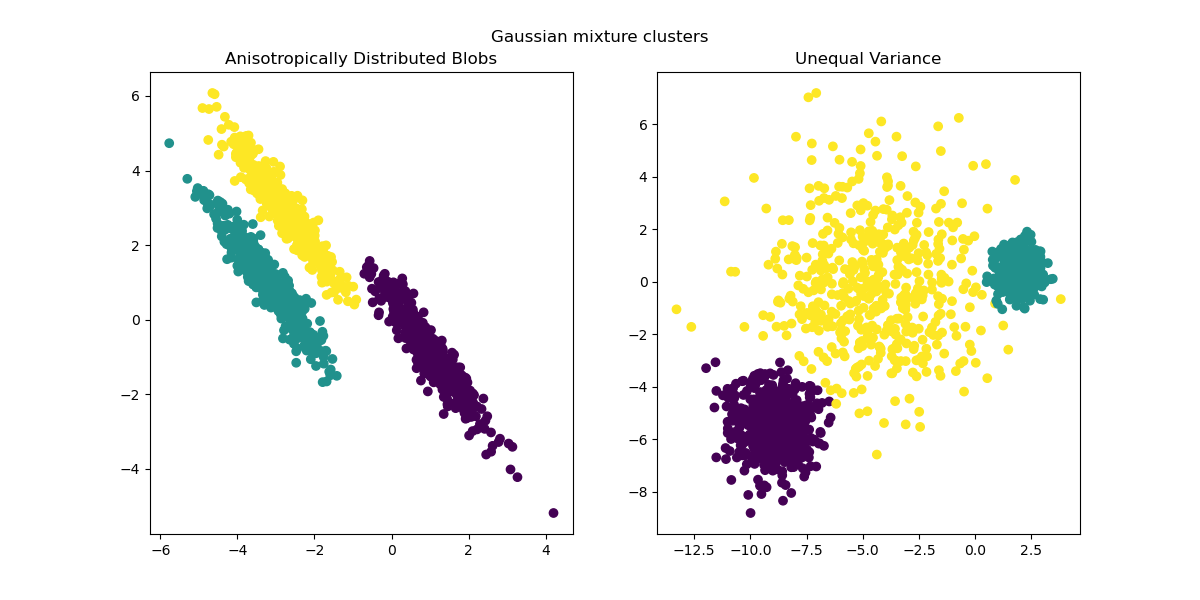
Поскольку анизотропные и неравные дисперсии являются реальными ограничениями алгоритма k-средних, здесь мы предлагаем вместо этого использование
GaussianMixture, который также предполагает гауссовские кластеры, но не накладывает ограничений на их дисперсии. Обратите внимание, что все еще необходимо найти правильное количество кластеров (см.
Выбор модели гауссовской смеси).
Пример того, как другие методы кластеризации работают с анизотропными или неравными дисперсионными сгустками, см. в примере Сравнение различных алгоритмов кластеризации на игрушечных наборах данных.
from sklearn.mixture import GaussianMixture
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
y_pred = GaussianMixture(n_components=3).fit_predict(X_aniso)
ax1.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
ax1.set_title("Anisotropically Distributed Blobs")
y_pred = GaussianMixture(n_components=3).fit_predict(X_varied)
ax2.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
ax2.set_title("Unequal Variance")
plt.suptitle("Gaussian mixture clusters").set_y(0.95)
plt.show()
Заключительные замечания#
В многомерных пространствах евклидовы расстояния имеют тенденцию увеличиваться (не показано в этом примере). Запуск алгоритма уменьшения размерности перед кластеризацией k-means может смягчить эту проблему и ускорить вычисления (см. пример Кластеризация текстовых документов с использованием k-means).
В случае, когда известно, что кластеры изотропны, имеют схожую дисперсию и не слишком разрежены, алгоритм k-средних довольно эффективен и является одним из самых быстрых доступных алгоритмов кластеризации. Это преимущество теряется, если приходится перезапускать его несколько раз, чтобы избежать сходимости к локальному минимуму.
Общее время выполнения скрипта: (0 минут 0.968 секунд)
Связанные примеры
Сравнение производительности биссекционного K-средних и обычного K-средних
Сравнение различных методов иерархической связи на игрушечных наборах данных
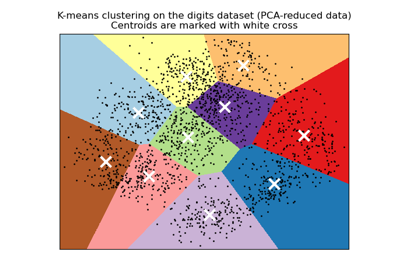
Демонстрация кластеризации K-Means на данных рукописных цифр