Сегментация изображения греческих монет на регионы

В этом примере используется Спектральная кластеризация на графе, созданном из разницы между вокселями на изображении, чтобы разбить это изображение на несколько частично однородных областей.

Эта процедура (спектральная кластеризация на изображении) является эффективным приближённым решением для нахождения нормализованных разрезов графа.

Существует три варианта назначения меток:

• ‘kmeans’ спектральная кластеризация группирует образцы в пространстве вложений используя алгоритм kmeans

• ‘discrete’ итеративно ищет ближайшее пространство разбиения к пространству вложения спектральной кластеризации.

• ‘cluster_qr’ назначает метки с использованием QR-факторизации с поворотом, которая напрямую определяет разделение в пространстве вложений.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time

import matplotlib.pyplot as plt
import numpy as np
from scipy.ndimage import gaussian_filter
from skimage.data import coins
from skimage.transform import rescale

from sklearn.cluster import spectral_clustering
from sklearn.feature_extraction import image

# load the coins as a numpy array
orig_coins = coins()

# Resize it to 20% of the original size to speed up the processing
# Applying a Gaussian filter for smoothing prior to down-scaling
# reduces aliasing artifacts.
smoothened_coins = gaussian_filter(orig_coins, sigma=2)
rescaled_coins = rescale(smoothened_coins, 0.2, mode="reflect", anti_aliasing=False)

# Convert the image into a graph with the value of the gradient on the
# edges.
graph = image.img_to_graph(rescaled_coins)

# Take a decreasing function of the gradient: an exponential
# The smaller beta is, the more independent the segmentation is of the
# actual image. For beta=1, the segmentation is close to a voronoi
beta = 10
eps = 1e-6
graph.data = np.exp(-beta * graph.data / graph.data.std()) + eps

# The number of segmented regions to display needs to be chosen manually.
# The current version of 'spectral_clustering' does not support determining
# the number of good quality clusters automatically.
n_regions = 26

Вычислить и визуализировать полученные регионы

# Computing a few extra eigenvectors may speed up the eigen_solver.
# The spectral clustering quality may also benefit from requesting
# extra regions for segmentation.
n_regions_plus = 3

# Apply spectral clustering using the default eigen_solver='arpack'.
# Any implemented solver can be used: eigen_solver='arpack', 'lobpcg', or 'amg'.
# Choosing eigen_solver='amg' requires an extra package called 'pyamg'.
# The quality of segmentation and the speed of calculations is mostly determined
# by the choice of the solver and the value of the tolerance 'eigen_tol'.
# TODO: varying eigen_tol seems to have no effect for 'lobpcg' and 'amg' #21243.
for assign_labels in ("kmeans", "discretize", "cluster_qr"):
    t0 = time.time()
    labels = spectral_clustering(
        graph,
        n_clusters=(n_regions + n_regions_plus),
        eigen_tol=1e-7,
        assign_labels=assign_labels,
        random_state=42,
    )

    t1 = time.time()
    labels = labels.reshape(rescaled_coins.shape)
    plt.figure(figsize=(5, 5))
    plt.imshow(rescaled_coins, cmap=plt.cm.gray)

    plt.xticks(())
    plt.yticks(())
    title = "Spectral clustering: %s, %.2fs" % (assign_labels, (t1 - t0))
    print(title)
    plt.title(title)
    for l in range(n_regions):
        colors = [plt.cm.nipy_spectral((l + 4) / float(n_regions + 4))]
        plt.contour(labels == l, colors=colors)
        # To view individual segments as appear comment in plt.pause(0.5)
plt.show()

# TODO: After #21194 is merged and #21243 is fixed, check which eigen_solver
# is the best and set eigen_solver='arpack', 'lobpcg', or 'amg' and eigen_tol
# explicitly in this example.

• 
• 
• 

Spectral clustering: kmeans, 1.76s
Spectral clustering: discretize, 1.62s
Spectral clustering: cluster_qr, 1.56s

Связанные примеры

Спектральная кластеризация для сегментации изображений

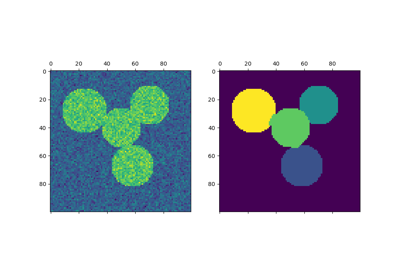
Спектральная кластеризация для сегментации изображений

Демонстрация структурированной иерархической кластеризации Уорда на изображении монет

Демонстрация структурированной иерархической кластеризации Уорда на изображении монет

Визуализация структуры фондового рынка

Визуализация структуры фондового рынка

Удаление шума изображений с использованием обучения словаря

Удаление шума изображений с использованием обучения словаря