Примечание

Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.

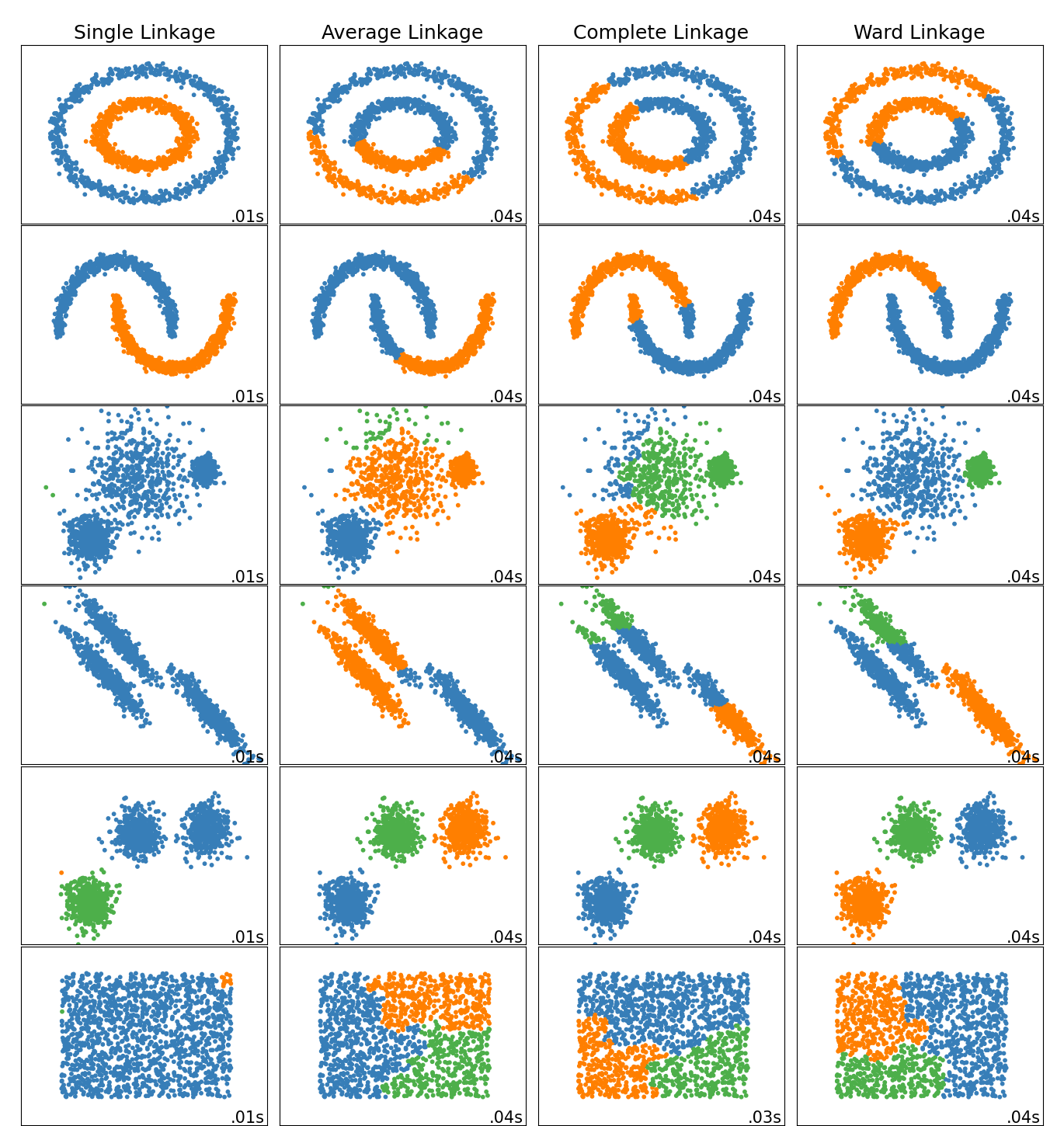
Сравнение различных методов иерархической связи на игрушечных наборах данных#

Этот пример показывает характеристики различных методов связывания для иерархической кластеризации на наборах данных, которые "интересны", но все еще в 2D.

Основные наблюдения, которые следует сделать:

одиночная связь быстрая и может хорошо работать с неглобулярными данными, но плохо справляется с наличием шума.
средняя и полная связь хорошо работают на четко разделенных глобулярных кластерах, но дают смешанные результаты в остальных случаях.
Метод Ward наиболее эффективен для зашумленных данных.

Хотя эти примеры дают некоторое представление об алгоритмах, это представление может не применяться к данным очень высокой размерности.

# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause

import time
import warnings
from itertools import cycle, islice

import matplotlib.pyplot as plt
import numpy as np

from sklearn import cluster, datasets
from sklearn.preprocessing import StandardScaler

Генерировать наборы данных. Мы выбираем размер достаточно большим, чтобы увидеть масштабируемость алгоритмов, но не слишком большим, чтобы избежать слишком долгого времени выполнения

n_samples = 1500
noisy_circles = datasets.make_circles(
    n_samples=n_samples, factor=0.5, noise=0.05, random_state=170
)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=0.05, random_state=170)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=170)
rng = np.random.RandomState(170)
no_structure = rng.rand(n_samples, 2), None

# Anisotropicly distributed data
X, y = datasets.make_blobs(n_samples=n_samples, random_state=170)
transformation = [[0.6, -0.6], [-0.4, 0.8]]
X_aniso = np.dot(X, transformation)
aniso = (X_aniso, y)

# blobs with varied variances
varied = datasets.make_blobs(
    n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=170
)

Запустить кластеризацию и построить график

# Set up cluster parameters
plt.figure(figsize=(9 * 1.3 + 2, 14.5))
plt.subplots_adjust(
    left=0.02, right=0.98, bottom=0.001, top=0.96, wspace=0.05, hspace=0.01
)

plot_num = 1

default_base = {"n_neighbors": 10, "n_clusters": 3}

datasets = [
    (noisy_circles, {"n_clusters": 2}),
    (noisy_moons, {"n_clusters": 2}),
    (varied, {"n_neighbors": 2}),
    (aniso, {"n_neighbors": 2}),
    (blobs, {}),
    (no_structure, {}),
]

for i_dataset, (dataset, algo_params) in enumerate(datasets):
    # update parameters with dataset-specific values
    params = default_base.copy()
    params.update(algo_params)

    X, y = dataset

    # normalize dataset for easier parameter selection
    X = StandardScaler().fit_transform(X)

    # ============
    # Create cluster objects
    # ============
    ward = cluster.AgglomerativeClustering(
        n_clusters=params["n_clusters"], linkage="ward"
    )
    complete = cluster.AgglomerativeClustering(
        n_clusters=params["n_clusters"], linkage="complete"
    )
    average = cluster.AgglomerativeClustering(
        n_clusters=params["n_clusters"], linkage="average"
    )
    single = cluster.AgglomerativeClustering(
        n_clusters=params["n_clusters"], linkage="single"
    )

    clustering_algorithms = (
        ("Single Linkage", single),
        ("Average Linkage", average),
        ("Complete Linkage", complete),
        ("Ward Linkage", ward),
    )

    for name, algorithm in clustering_algorithms:
        t0 = time.time()

        # catch warnings related to kneighbors_graph
        with warnings.catch_warnings():
            warnings.filterwarnings(
                "ignore",
                message="the number of connected components of the "
                "connectivity matrix is [0-9]{1,2}"
                " > 1. Completing it to avoid stopping the tree early.",
                category=UserWarning,
            )
            algorithm.fit(X)

        t1 = time.time()
        if hasattr(algorithm, "labels_"):
            y_pred = algorithm.labels_.astype(int)
        else:
            y_pred = algorithm.predict(X)

        plt.subplot(len(datasets), len(clustering_algorithms), plot_num)
        if i_dataset == 0:
            plt.title(name, size=18)

        colors = np.array(
            list(
                islice(
                    cycle(
                        [
                            "#377eb8",
                            "#ff7f00",
                            "#4daf4a",
                            "#f781bf",
                            "#a65628",
                            "#984ea3",
                            "#999999",
                            "#e41a1c",
                            "#dede00",
                        ]
                    ),
                    int(max(y_pred) + 1),
                )
            )
        )
        plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])

        plt.xlim(-2.5, 2.5)
        plt.ylim(-2.5, 2.5)
        plt.xticks(())
        plt.yticks(())
        plt.text(
            0.99,
            0.01,
            ("%.2fs" % (t1 - t0)).lstrip("0"),
            transform=plt.gca().transAxes,
            size=15,
            horizontalalignment="right",
        )
        plot_num += 1

plt.show()