Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Graham Clenaghan#
Этот пример демонстрирует class_likelihood_ratios
функция, которая вычисляет положительные и отрицательные отношения правдоподобия (LR+,
LR-) для оценки прогностической способности бинарного классификатора. Как мы увидим,
эти метрики не зависят от пропорции классов в тестовом наборе,
что делает их очень полезными, когда доступные данные для исследования имеют другую
пропорцию классов, чем целевое приложение.
Типичное использование — это исследование случай-контроль в медицине, где классы почти сбалансированы, в то время как в общей популяции наблюдается большой дисбаланс классов. В таком применении предтестовая вероятность наличия у индивидуума целевого состояния может быть выбрана равной распространенности, т.е. доле конкретной популяции, у которой обнаружено медицинское состояние. Послетестовые вероятности тогда представляют вероятность того, что состояние действительно присутствует при положительном результате теста.
В этом примере мы сначала обсудим связь между априорными и апостериорными шансами, задаваемую Отношения правдоподобия классов. Затем мы оцениваем их поведение в некоторых контролируемых сценариях. В последнем разделе мы строим их графики в зависимости от распространённости положительного класса.
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Анализ до теста и после теста#
Предположим, у нас есть популяция субъектов с физиологическими измерениями X
которые, возможно, могут служить косвенными биомаркерами заболевания и фактическими индикаторами болезни y (истинные значения). Большинство людей в популяции
не являются носителями болезни, но меньшинство (в данном случае около 10%) являются:
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=10_000, weights=[0.9, 0.1], random_state=0)
print(f"Percentage of people carrying the disease: {100 * y.mean():.2f}%")
Percentage of people carrying the disease: 10.37%
Модель машинного обучения строится для диагностики, есть ли у человека с некоторыми заданными физиологическими измерениями вероятность наличия интересующего заболевания. Для оценки модели нам нужно оценить её производительность на отложенном тестовом наборе:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
Затем мы можем обучить нашу модель диагностики и вычислить положительное отношение правдоподобия, чтобы оценить полезность этого классификатора как инструмента диагностики заболевания:
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import class_likelihood_ratios
estimator = LogisticRegression().fit(X_train, y_train)
y_pred = estimator.predict(X_test)
pos_LR, neg_LR = class_likelihood_ratios(y_test, y_pred, replace_undefined_by=1.0)
print(f"LR+: {pos_LR:.3f}")
LR+: 12.617
Поскольку отношение правдоподобия положительного класса значительно больше 1.0, это означает, что инструмент диагностики на основе машинного обучения полезен: апостериорные шансы того, что состояние действительно присутствует при положительном результате теста, более чем в 12 раз превышают априорные шансы.
Кросс-валидация отношений правдоподобия#
Мы оцениваем изменчивость измерений для отношений правдоподобия классов в некоторых конкретных случаях.
import pandas as pd
def scoring(estimator, X, y):
y_pred = estimator.predict(X)
pos_lr, neg_lr = class_likelihood_ratios(y, y_pred, replace_undefined_by=1.0)
return {"positive_likelihood_ratio": pos_lr, "negative_likelihood_ratio": neg_lr}
def extract_score(cv_results):
lr = pd.DataFrame(
{
"positive": cv_results["test_positive_likelihood_ratio"],
"negative": cv_results["test_negative_likelihood_ratio"],
}
)
return lr.aggregate(["mean", "std"])
Сначала мы проверяем LogisticRegression модель
со значениями гиперпараметров по умолчанию, как в предыдущем разделе.
from sklearn.model_selection import cross_validate
estimator = LogisticRegression()
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
Мы подтверждаем, что модель полезна: апостериорные шансы в 12-20 раз выше априорных шансов.
Напротив, рассмотрим фиктивный (dummy) модель, которая будет выдавать случайные предсказания с вероятностями, аналогичными средней распространённости заболевания в обучающей выборке:
from sklearn.dummy import DummyClassifier
estimator = DummyClassifier(strategy="stratified", random_state=1234)
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
Здесь оба отношения правдоподобия классов совместимы с 1.0, что делает этот классификатор бесполезным в качестве диагностического инструмента для улучшения обнаружения заболеваний.
Другой вариант для фиктивной модели — всегда предсказывать наиболее частый класс, который в данном случае является "без болезни".
estimator = DummyClassifier(strategy="most_frequent")
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
No samples were predicted for the positive class and `positive_likelihood_ratio` is set to `np.nan`. Use the `replace_undefined_by` param to
Отсутствие положительных прогнозов означает, что не будет ни истинно положительных, ни
ложноположительных результатов, что приводит к неопределенному LR+ которые ни в коем случае не должны интерпретироваться как бесконечные LR+ (классификатор идеально идентифицирует положительные случаи). В такой ситуации
class_likelihood_ratios функция возвращает nan и выдает предупреждение по умолчанию. Действительно, значение LR- помогает нам отбросить эту
модель.
Аналогичный сценарий может возникнуть при кросс-валидации сильно несбалансированных данных с малым количеством образцов: некоторые фолды не будут содержать образцов с заболеванием и, следовательно, не выдадут ни истинно положительных, ни ложно отрицательных результатов при использовании для тестирования. Математически это приводит к бесконечному LR+, что также не следует интерпретировать как идеальную идентификацию моделью положительных случаев. Такое событие приводит к более высокой дисперсии оценённых отношений правдоподобия, но всё же может интерпретироваться как увеличение пост-тестовых шансов наличия условия.
estimator = LogisticRegression()
X, y = make_classification(n_samples=300, weights=[0.9, 0.1], random_state=0)
extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
`positive_likelihood_ratio` is ill-defined and set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
`positive_likelihood_ratio` is ill-defined and set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
`positive_likelihood_ratio` is ill-defined and set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
`positive_likelihood_ratio` is ill-defined and set to `np.nan`. Use the `replace_undefined_by` param to
/home/circleci/project/sklearn/utils/_param_validation.py:218: UndefinedMetricWarning:
`positive_likelihood_ratio` is ill-defined and set to `np.nan`. Use the `replace_undefined_by` param to
является пользовательской функцией.#
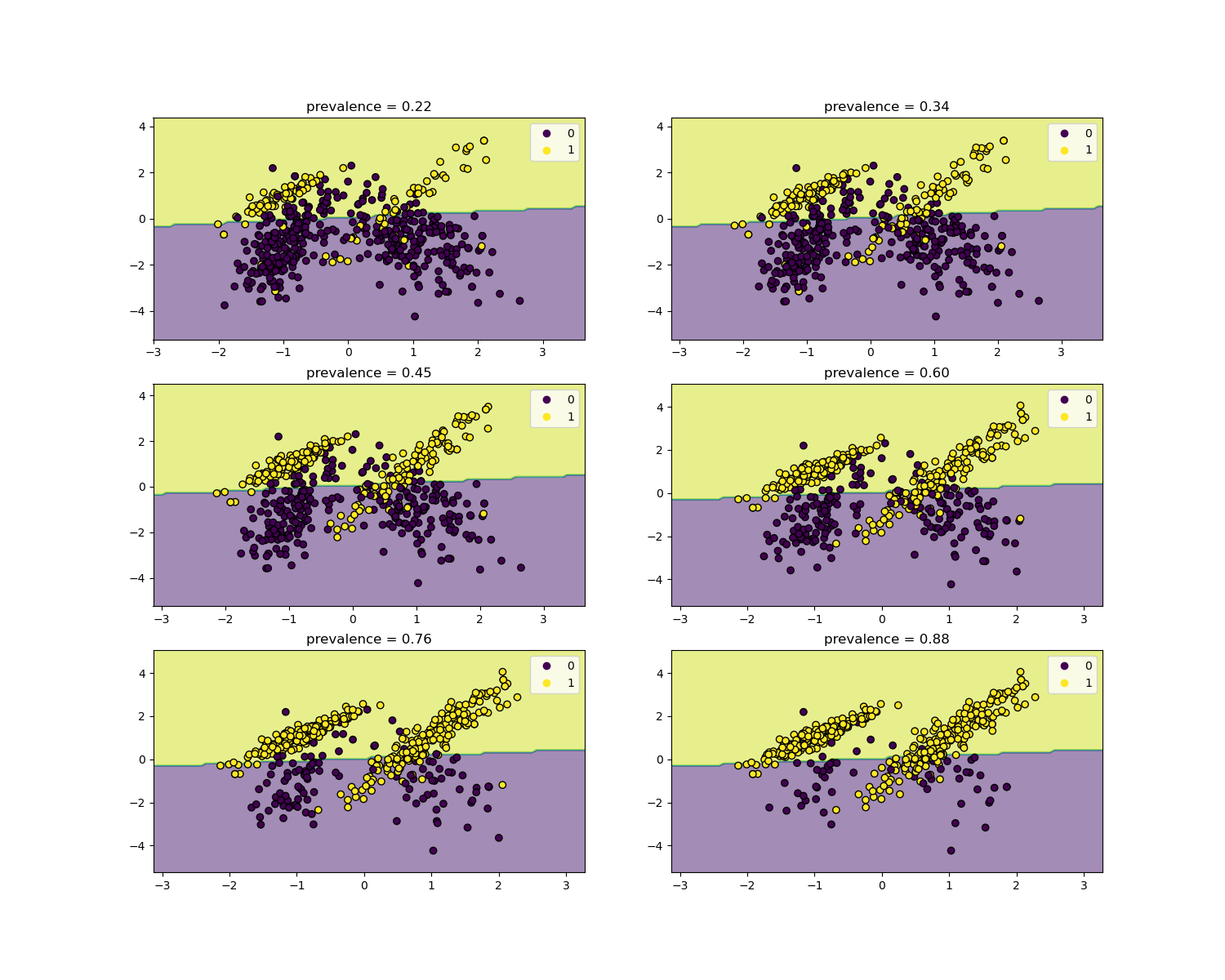
Отношения правдоподобия не зависят от распространенности заболевания и могут быть экстраполированы между популяциями независимо от любого возможного дисбаланса классов, при условии, что одна и та же модель применяется ко всем из них. Обратите внимание, что на графиках ниже граница принятия решений постоянна (см. SVM: Разделяющая гиперплоскость для несбалансированных классов для исследования границы решения для несбалансированных классов).
Здесь мы обучаем LogisticRegression базовая модель на основе исследования случай-контроль с распространенностью 50%. Затем она оценивается на популяциях с различной распространенностью. Мы используем
make_classification функция для обеспечения того, чтобы процесс генерации данных всегда был одинаковым, как показано на графиках ниже. Метка 1 соответствует положительному классу «заболевание», тогда как метка 0
означает «нет болезни».
from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np
from sklearn.inspection import DecisionBoundaryDisplay
populations = defaultdict(list)
common_params = {
"n_samples": 10_000,
"n_features": 2,
"n_informative": 2,
"n_redundant": 0,
"random_state": 0,
}
weights = np.linspace(0.1, 0.8, 6)
weights = weights[::-1]
# fit and evaluate base model on balanced classes
X, y = make_classification(**common_params, weights=[0.5, 0.5])
estimator = LogisticRegression().fit(X, y)
lr_base = extract_score(cross_validate(estimator, X, y, scoring=scoring, cv=10))
pos_lr_base, pos_lr_base_std = lr_base["positive"].values
neg_lr_base, neg_lr_base_std = lr_base["negative"].values
Теперь мы покажем границу решения для каждого уровня распространённости. Обратите внимание, что мы строим график только подмножества исходных данных, чтобы лучше оценить границу решения линейной модели.
fig, axs = plt.subplots(nrows=3, ncols=2, figsize=(15, 12))
for ax, (n, weight) in zip(axs.ravel(), enumerate(weights)):
X, y = make_classification(
**common_params,
weights=[weight, 1 - weight],
)
prevalence = y.mean()
populations["prevalence"].append(prevalence)
populations["X"].append(X)
populations["y"].append(y)
# down-sample for plotting
rng = np.random.RandomState(1)
plot_indices = rng.choice(np.arange(X.shape[0]), size=500, replace=True)
X_plot, y_plot = X[plot_indices], y[plot_indices]
# plot fixed decision boundary of base model with varying prevalence
disp = DecisionBoundaryDisplay.from_estimator(
estimator,
X_plot,
response_method="predict",
alpha=0.5,
ax=ax,
)
scatter = disp.ax_.scatter(X_plot[:, 0], X_plot[:, 1], c=y_plot, edgecolor="k")
disp.ax_.set_title(f"prevalence = {y_plot.mean():.2f}")
disp.ax_.legend(*scatter.legend_elements())
Мы определяем функцию для бутстреппинга.
def scoring_on_bootstrap(estimator, X, y, rng, n_bootstrap=100):
results_for_prevalence = defaultdict(list)
for _ in range(n_bootstrap):
bootstrap_indices = rng.choice(
np.arange(X.shape[0]), size=X.shape[0], replace=True
)
for key, value in scoring(
estimator, X[bootstrap_indices], y[bootstrap_indices]
).items():
results_for_prevalence[key].append(value)
return pd.DataFrame(results_for_prevalence)
Мы оцениваем базовую модель для каждой распространенности с помощью бутстрапинга.
results = defaultdict(list)
n_bootstrap = 100
rng = np.random.default_rng(seed=0)
for prevalence, X, y in zip(
populations["prevalence"], populations["X"], populations["y"]
):
results_for_prevalence = scoring_on_bootstrap(
estimator, X, y, rng, n_bootstrap=n_bootstrap
)
results["prevalence"].append(prevalence)
results["metrics"].append(
results_for_prevalence.aggregate(["mean", "std"]).unstack()
)
results = pd.DataFrame(results["metrics"], index=results["prevalence"])
results.index.name = "prevalence"
results
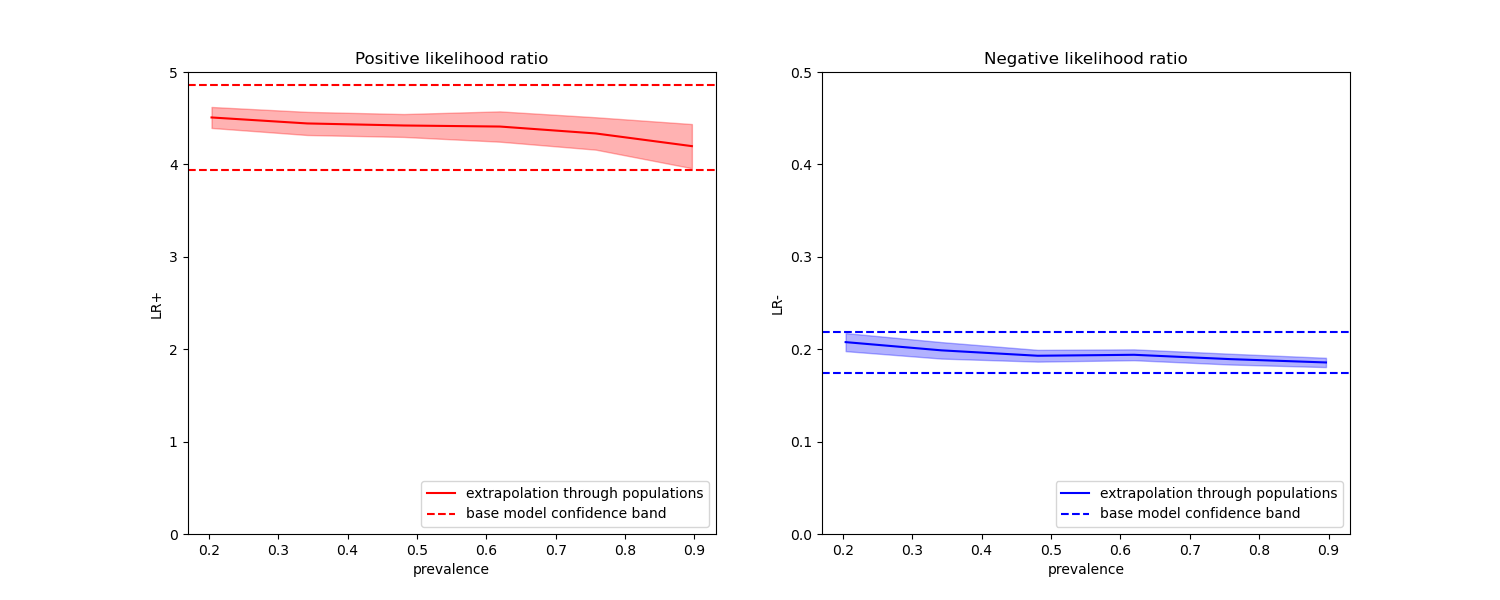
На графиках ниже мы видим, что отношения правдоподобия классов, пересчитанные с разными распространённостями, действительно постоянны в пределах одного стандартного отклонения от значений, вычисленных на сбалансированных классах.
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(15, 6))
results["positive_likelihood_ratio"]["mean"].plot(
ax=ax1, color="r", label="extrapolation through populations"
)
ax1.axhline(y=pos_lr_base + pos_lr_base_std, color="r", linestyle="--")
ax1.axhline(
y=pos_lr_base - pos_lr_base_std,
color="r",
linestyle="--",
label="base model confidence band",
)
ax1.fill_between(
results.index,
results["positive_likelihood_ratio"]["mean"]
- results["positive_likelihood_ratio"]["std"],
results["positive_likelihood_ratio"]["mean"]
+ results["positive_likelihood_ratio"]["std"],
color="r",
alpha=0.3,
)
ax1.set(
title="Positive likelihood ratio",
ylabel="LR+",
ylim=[0, 5],
)
ax1.legend(loc="lower right")
ax2 = results["negative_likelihood_ratio"]["mean"].plot(
ax=ax2, color="b", label="extrapolation through populations"
)
ax2.axhline(y=neg_lr_base + neg_lr_base_std, color="b", linestyle="--")
ax2.axhline(
y=neg_lr_base - neg_lr_base_std,
color="b",
linestyle="--",
label="base model confidence band",
)
ax2.fill_between(
results.index,
results["negative_likelihood_ratio"]["mean"]
- results["negative_likelihood_ratio"]["std"],
results["negative_likelihood_ratio"]["mean"]
+ results["negative_likelihood_ratio"]["std"],
color="b",
alpha=0.3,
)
ax2.set(
title="Negative likelihood ratio",
ylabel="LR-",
ylim=[0, 0.5],
)
ax2.legend(loc="lower right")
plt.show()
Общее время выполнения скрипта: (0 минут 1.721 секунд)
Связанные примеры
Пост-фактумная настройка точки отсечения функции принятия решений