Примечание
Перейти в конец чтобы скачать полный пример кода или запустить этот пример в браузере через JupyterLite или Binder.
Многоклассовая рабочая характеристика приемника (ROC)#
В этом примере описывается использование метрики Receiver Operating Characteristic (ROC) для оценки качества многоклассовых классификаторов.
Кривые ROC обычно имеют истинно положительную частоту (TPR) на оси Y и ложноположительную частоту (FPR) на оси X. Это означает, что верхний левый угол графика является «идеальной» точкой - FPR равен нулю, а TPR равен единице. Это не очень реалистично, но означает, что большая площадь под кривой (AUC) обычно лучше. «Крутизна» кривых ROC также важна, поскольку идеально максимизировать TPR, минимизируя FPR.
Кривые ROC обычно используются в бинарной классификации, где TPR и FPR могут быть определены однозначно. В случае многоклассовой классификации понятие TPR или FPR получается только после бинаризации вывода. Это можно сделать двумя разными способами:
схема One-vs-Rest сравнивает каждый класс со всеми остальными (рассматриваемыми как один);
схема "Один против одного" сравнивает каждую уникальную попарную комбинацию классов.
В этом примере мы исследуем обе схемы и демонстрируем концепции микро- и макроусреднения как различных способов обобщения информации о ROC-кривых для многоклассовой классификации.
Примечание
См. Рабочая характеристика приёмника (ROC) с перекрёстной проверкой (Поэлементная L1 норма)
# Authors: The scikit-learn developers
# SPDX-License-Identifier: BSD-3-Clause
Загрузка и подготовка данных#
Мы импортируем Набор данных о растениях ириса который содержит 3 класса, каждый из которых соответствует типу растения ирис. Один класс линейно отделим от двух других; последние не линейно разделимы друг от друга.
Здесь мы бинаризуем вывод и добавляем зашумленные признаки, чтобы усложнить задачу.
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
iris = load_iris()
target_names = iris.target_names
X, y = iris.data, iris.target
y = iris.target_names[y]
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
n_classes = len(np.unique(y))
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)
(
X_train,
X_test,
y_train,
y_test,
) = train_test_split(X, y, test_size=0.5, stratify=y, random_state=0)
Мы обучаем LogisticRegression модель, которая может естественным образом обрабатывать многоклассовые задачи благодаря использованию мультиномиальной формулировки.
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression()
y_score = classifier.fit(X_train, y_train).predict_proba(X_test)
Многоклассовый ROC по схеме один-против-всех#
Многоклассовая стратегия "Один против остальных" (OvR), также известная как one-vs-all,
заключается в вычислении ROC-кривой для каждого из n_classes. На каждом шаге определенный класс рассматривается как положительный, а остальные классы рассматриваются как отрицательные в совокупности.
Примечание
Не следует путать стратегию OvR, используемую для оценка
многоклассовых классификаторов со стратегией OvR, используемой для обучать многоклассовый классификатор путем подгонки набора бинарных классификаторов (например,
через OneVsRestClassifier мета-оценщика).
Оценку OvR ROC можно использовать для тщательного анализа любых моделей
классификации независимо от того, как они были обучены (см. Многоклассовые и многомерные алгоритмы).
В этом разделе мы используем LabelBinarizer для бинаризации целевой переменной с помощью one-hot-кодирования в стиле OvR. Это означает, что цель формы (n_samples,) отображается в цель формы (n_samples,
n_classes).
from sklearn.preprocessing import LabelBinarizer
label_binarizer = LabelBinarizer().fit(y_train)
y_onehot_test = label_binarizer.transform(y_test)
y_onehot_test.shape # (n_samples, n_classes)
(75, 3)
Мы также можем легко проверить кодировку конкретного класса:
label_binarizer.transform(["virginica"])
array([[0, 0, 1]])
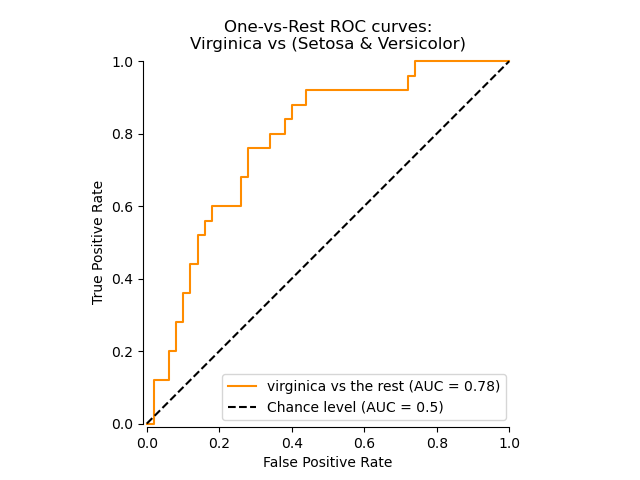
Кривая ROC, показывающая конкретный класс#
На следующем графике мы показываем результирующую кривую ROC при рассмотрении цветков ириса как «virginica» (class_id=2) или "не virginica" (остальные).
class_of_interest = "virginica"
class_id = np.flatnonzero(label_binarizer.classes_ == class_of_interest)[0]
class_id
np.int64(2)
import matplotlib.pyplot as plt
from sklearn.metrics import RocCurveDisplay
display = RocCurveDisplay.from_predictions(
y_onehot_test[:, class_id],
y_score[:, class_id],
name=f"{class_of_interest} vs the rest",
curve_kwargs=dict(color="darkorange"),
plot_chance_level=True,
despine=True,
)
_ = display.ax_.set(
xlabel="False Positive Rate",
ylabel="True Positive Rate",
title="One-vs-Rest ROC curves:\nVirginica vs (Setosa & Versicolor)",
)
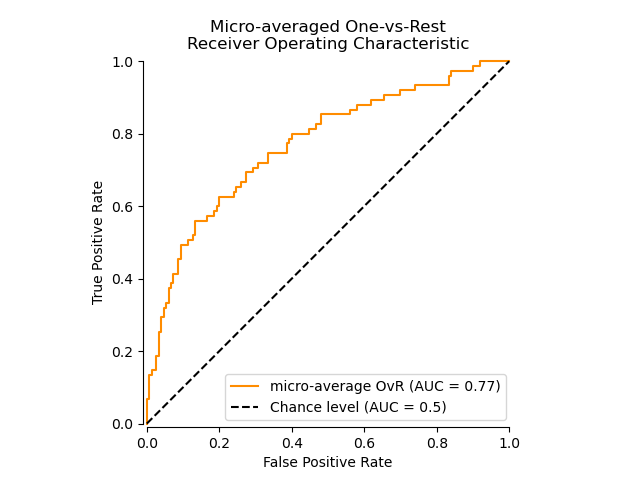
ROC-кривая с использованием микроусреднения OvR#
Микро-усреднение агрегирует вклады от всех классов (используя
numpy.ravel) для вычисления средних метрик следующим образом:
\(TPR=\frac{\sum_{c}TP_c}{\sum_{c}(TP_c + FN_c)}\) ;
\(FPR=\frac{\sum_{c}FP_c}{\sum_{c}(FP_c + TN_c)}\) .
Мы можем кратко продемонстрировать эффект numpy.ravel:
print(f"y_score:\n{y_score[0:2, :]}")
print()
print(f"y_score.ravel():\n{y_score[0:2, :].ravel()}")
y_score:
[[0.38 0.05 0.57]
[0.07 0.28 0.65]]
y_score.ravel():
[0.38 0.05 0.57 0.07 0.28 0.65]
В настройке многоклассовой классификации с сильно несбалансированными классами микро-усреднение предпочтительнее макро-усреднения. В таких случаях можно альтернативно использовать взвешенное макро-усреднение, не показанное здесь.
display = RocCurveDisplay.from_predictions(
y_onehot_test.ravel(),
y_score.ravel(),
name="micro-average OvR",
curve_kwargs=dict(color="darkorange"),
plot_chance_level=True,
despine=True,
)
_ = display.ax_.set(
xlabel="False Positive Rate",
ylabel="True Positive Rate",
title="Micro-averaged One-vs-Rest\nReceiver Operating Characteristic",
)
В случае, когда основной интерес представляет не график, а сама оценка ROC-AUC,
мы можем воспроизвести значение, показанное на графике, используя
roc_auc_score.
from sklearn.metrics import roc_auc_score
micro_roc_auc_ovr = roc_auc_score(
y_test,
y_score,
multi_class="ovr",
average="micro",
)
print(f"Micro-averaged One-vs-Rest ROC AUC score:\n{micro_roc_auc_ovr:.2f}")
Micro-averaged One-vs-Rest ROC AUC score:
0.77
Это эквивалентно вычислению ROC-кривой с
roc_curve и затем площадь под кривой с
auc для распакованных истинных и предсказанных классов.
from sklearn.metrics import auc, roc_curve
# store the fpr, tpr, and roc_auc for all averaging strategies
fpr, tpr, roc_auc = dict(), dict(), dict()
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_onehot_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
print(f"Micro-averaged One-vs-Rest ROC AUC score:\n{roc_auc['micro']:.2f}")
Micro-averaged One-vs-Rest ROC AUC score:
0.77
Примечание
По умолчанию, вычисление ROC-кривой добавляет одну точку при максимальной частоте ложных срабатываний, используя линейную интерполяцию и поправку Макклиша [Анализ части кривой ROC Med Decis Making. 1989 Jul-Sep; 9(3):190-5.].
ROC-кривую с использованием макро-усреднения OvR#
Получение макро-среднего требует вычисления метрики независимо для каждого класса, а затем усреднения по ним, тем самым априори рассматривая все классы одинаково. Сначала мы агрегируем истинные/ложные положительные частоты по классам:
\(TPR=\frac{1}{C}\sum_{c}\frac{TP_c}{TP_c + FN_c}\) ;
\(FPR=\frac{1}{C}\sum_{c}\frac{FP_c}{FP_c + TN_c}\) .
где C является общим количеством классов.
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_onehot_test[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
fpr_grid = np.linspace(0.0, 1.0, 1000)
# Interpolate all ROC curves at these points
mean_tpr = np.zeros_like(fpr_grid)
for i in range(n_classes):
mean_tpr += np.interp(fpr_grid, fpr[i], tpr[i]) # linear interpolation
# Average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = fpr_grid
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
print(f"Macro-averaged One-vs-Rest ROC AUC score:\n{roc_auc['macro']:.2f}")
Macro-averaged One-vs-Rest ROC AUC score:
0.78
Это вычисление эквивалентно простому вызову
macro_roc_auc_ovr = roc_auc_score(
y_test,
y_score,
multi_class="ovr",
average="macro",
)
print(f"Macro-averaged One-vs-Rest ROC AUC score:\n{macro_roc_auc_ovr:.2f}")
Macro-averaged One-vs-Rest ROC AUC score:
0.78
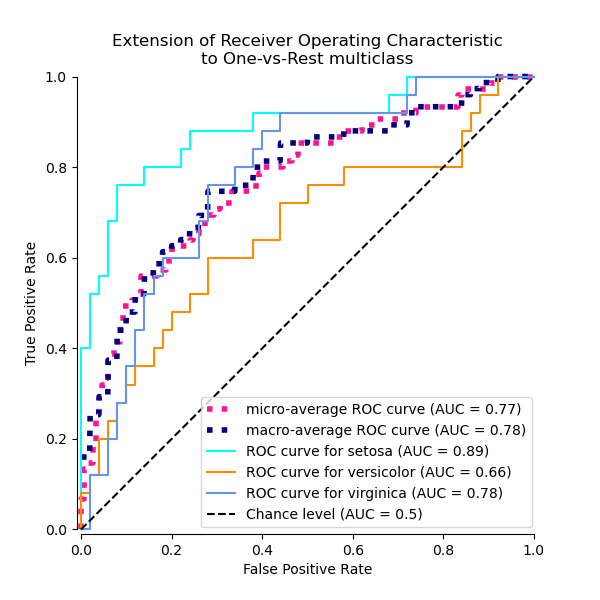
Построить все ROC-кривые OvR вместе#
from itertools import cycle
fig, ax = plt.subplots(figsize=(6, 6))
plt.plot(
fpr["micro"],
tpr["micro"],
label=f"micro-average ROC curve (AUC = {roc_auc['micro']:.2f})",
color="deeppink",
linestyle=":",
linewidth=4,
)
plt.plot(
fpr["macro"],
tpr["macro"],
label=f"macro-average ROC curve (AUC = {roc_auc['macro']:.2f})",
color="navy",
linestyle=":",
linewidth=4,
)
colors = cycle(["aqua", "darkorange", "cornflowerblue"])
for class_id, color in zip(range(n_classes), colors):
RocCurveDisplay.from_predictions(
y_onehot_test[:, class_id],
y_score[:, class_id],
name=f"ROC curve for {target_names[class_id]}",
curve_kwargs=dict(color=color),
ax=ax,
plot_chance_level=(class_id == 2),
despine=True,
)
_ = ax.set(
xlabel="False Positive Rate",
ylabel="True Positive Rate",
title="Extension of Receiver Operating Characteristic\nto One-vs-Rest multiclass",
)
Многоклассовый ROC по схеме "один против одного"#
Стратегия многоклассовой классификации "Один против одного" (OvO) заключается в обучении одного классификатора
для каждой пары классов. Поскольку требуется обучить n_classes * (n_classes - 1) / 2
классификаторов, этот метод обычно медленнее, чем One-vs-Rest, из-за его
O(n_classes ^2) сложность.
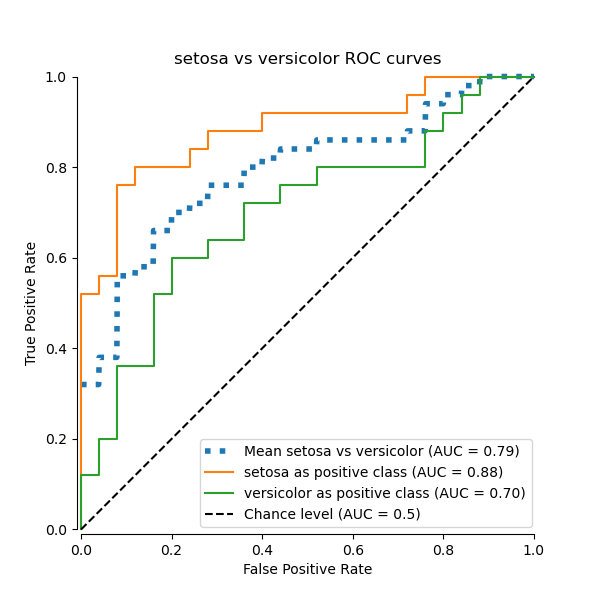
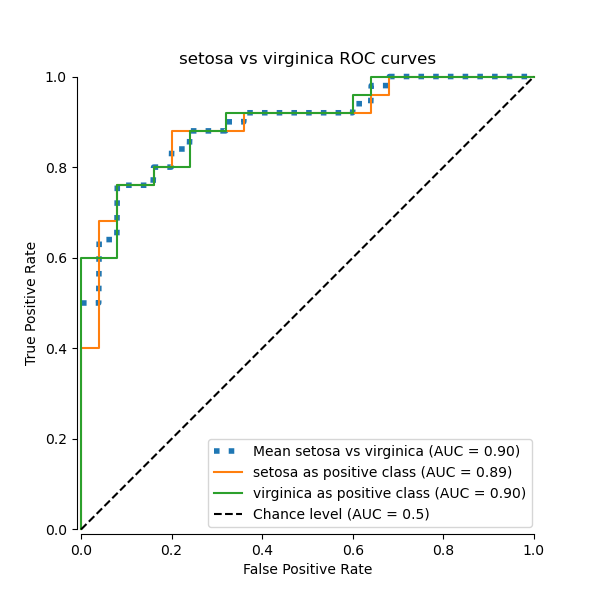
В этом разделе мы демонстрируем макроусредненную AUC, используя схему OvO для 3 возможных комбинаций в Набор данных о растениях ириса: «setosa» против «versicolor», «versicolor» против «virginica» и «virginica» против «setosa». Обратите внимание, что микроусреднение не определено для схемы OvO.
Кривая ROC с использованием макро-усреднения OvO#
В схеме OvO первый шаг — определить все возможные уникальные комбинации пар. Вычисление оценок выполняется путём рассмотрения одного из элементов в данной паре как положительного класса, а другого элемента как отрицательного класса, затем пересчёта оценки путём инверсии ролей и взятия среднего значения обеих оценок.
from itertools import combinations
pair_list = list(combinations(np.unique(y), 2))
print(pair_list)
[(np.str_('setosa'), np.str_('versicolor')), (np.str_('setosa'), np.str_('virginica')), (np.str_('versicolor'), np.str_('virginica'))]
pair_scores = []
mean_tpr = dict()
for ix, (label_a, label_b) in enumerate(pair_list):
a_mask = y_test == label_a
b_mask = y_test == label_b
ab_mask = np.logical_or(a_mask, b_mask)
a_true = a_mask[ab_mask]
b_true = b_mask[ab_mask]
idx_a = np.flatnonzero(label_binarizer.classes_ == label_a)[0]
idx_b = np.flatnonzero(label_binarizer.classes_ == label_b)[0]
fpr_a, tpr_a, _ = roc_curve(a_true, y_score[ab_mask, idx_a])
fpr_b, tpr_b, _ = roc_curve(b_true, y_score[ab_mask, idx_b])
mean_tpr[ix] = np.zeros_like(fpr_grid)
mean_tpr[ix] += np.interp(fpr_grid, fpr_a, tpr_a)
mean_tpr[ix] += np.interp(fpr_grid, fpr_b, tpr_b)
mean_tpr[ix] /= 2
mean_score = auc(fpr_grid, mean_tpr[ix])
pair_scores.append(mean_score)
fig, ax = plt.subplots(figsize=(6, 6))
plt.plot(
fpr_grid,
mean_tpr[ix],
label=f"Mean {label_a} vs {label_b} (AUC = {mean_score:.2f})",
linestyle=":",
linewidth=4,
)
RocCurveDisplay.from_predictions(
a_true,
y_score[ab_mask, idx_a],
ax=ax,
name=f"{label_a} as positive class",
)
RocCurveDisplay.from_predictions(
b_true,
y_score[ab_mask, idx_b],
ax=ax,
name=f"{label_b} as positive class",
plot_chance_level=True,
despine=True,
)
ax.set(
xlabel="False Positive Rate",
ylabel="True Positive Rate",
title=f"{target_names[idx_a]} vs {label_b} ROC curves",
)
print(f"Macro-averaged One-vs-One ROC AUC score:\n{np.average(pair_scores):.2f}")
Macro-averaged One-vs-One ROC AUC score:
0.78
Также можно утверждать, что макро-среднее, вычисленное "вручную", эквивалентно реализованному average="macro" опцию
roc_auc_score функция.
macro_roc_auc_ovo = roc_auc_score(
y_test,
y_score,
multi_class="ovo",
average="macro",
)
print(f"Macro-averaged One-vs-One ROC AUC score:\n{macro_roc_auc_ovo:.2f}")
Macro-averaged One-vs-One ROC AUC score:
0.78
Построить все ROC-кривые OvO вместе#
ovo_tpr = np.zeros_like(fpr_grid)
fig, ax = plt.subplots(figsize=(6, 6))
for ix, (label_a, label_b) in enumerate(pair_list):
ovo_tpr += mean_tpr[ix]
ax.plot(
fpr_grid,
mean_tpr[ix],
label=f"Mean {label_a} vs {label_b} (AUC = {pair_scores[ix]:.2f})",
)
ovo_tpr /= sum(1 for pair in enumerate(pair_list))
ax.plot(
fpr_grid,
ovo_tpr,
label=f"One-vs-One macro-average (AUC = {macro_roc_auc_ovo:.2f})",
linestyle=":",
linewidth=4,
)
ax.plot([0, 1], [0, 1], "k--", label="Chance level (AUC = 0.5)")
_ = ax.set(
xlabel="False Positive Rate",
ylabel="True Positive Rate",
title="Extension of Receiver Operating Characteristic\nto One-vs-One multiclass",
aspect="equal",
xlim=(-0.01, 1.01),
ylim=(-0.01, 1.01),
)
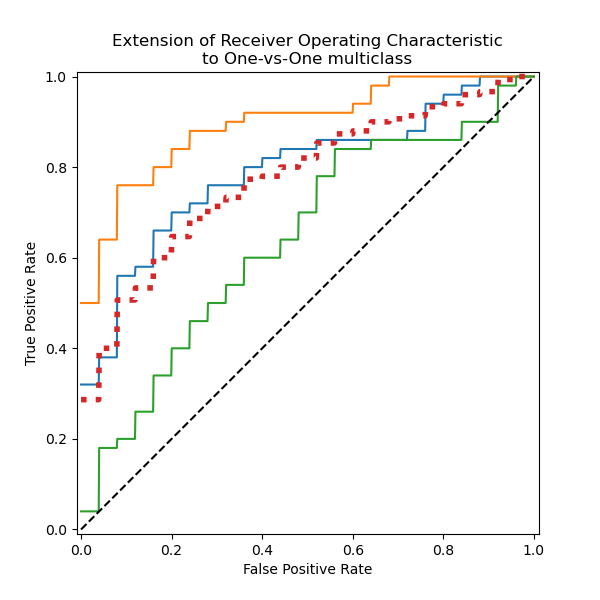
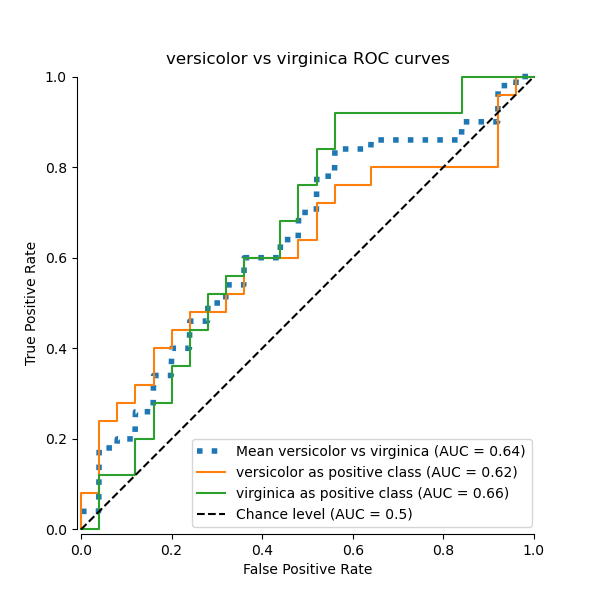
Мы подтверждаем, что классы «versicolor» и «virginica» плохо идентифицируются линейным классификатором. Обратите внимание, что ROC-AUC оценка для «virginica» против остальных (0.77) находится между оценками ROC-AUC OvO для «versicolor» против «virginica» (0.64) и «setosa» против «virginica» (0.90). Действительно, стратегия OvO предоставляет дополнительную информацию о путанице между парой классов, за счет вычислительных затрат при большом количестве классов.
Стратегия OvO рекомендуется, если пользователь в основном заинтересован в правильной идентификации определенного класса или подмножества классов, тогда как оценка общей производительности классификатора все еще может быть обобщена с помощью заданной стратегии усреднения.
При работе с несбалансированными наборами данных выбор подходящей метрики на основе бизнес-контекста или решаемой проблемы имеет решающее значение. Также важно выбрать подходящий метод усреднения (микро против макро) в зависимости от желаемого результата:
Микроусреднение агрегирует метрики по всем экземплярам, рассматривая каждый отдельный экземпляр одинаково, независимо от его класса. Этот подход полезен при оценке общей производительности, но обратите внимание, что он может доминировать со стороны большинства класса в несбалансированных наборах данных.
Макроусреднение вычисляет метрики для каждого класса независимо, а затем усредняет их, придавая одинаковый вес каждому классу. Это особенно полезно, когда вы хотите, чтобы недостаточно представленные классы считались такими же важными, как и высоконаселенные классы.
Общее время выполнения скрипта: (0 минут 0.561 секунд)
Связанные примеры
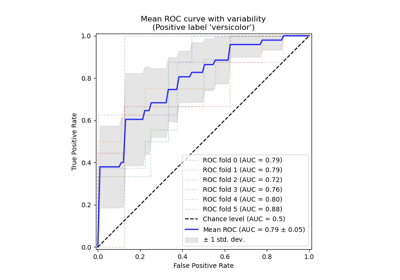
Рабочая характеристика приёмника (ROC) с перекрёстной проверкой